|
|
| Línea 1: |
Línea 1: |
| = Enunciado = | | ==Enunciado== |
| [[File:MRGIC-PercusionSobreVarilla-Enunciado.png|right|250px]]
| | Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal. |
| Una varilla delgada (sólido "2") de masa <math>m</math> y longitud <math>2b</math> está articulada
| |
| en un pasador (punto <math>A</math>) que desliza sobre el eje fijo <math>OY_1</math>.
| |
|
| |
|
| #Calcula la reducción cinemática en el punto <math>A</math> del movimiento {21}.
| | <center>[[Archivo:mano-hilo-pesa.jpg]]</center> |
| #Calcula la energía cinética de la varilla y su energía potencial.
| |
| #Cuando la varilla se encuentra en reposo y con <math>x=0</math> y <math>\theta=0</math>, se aplica en el punto <math>C</math> una percusión <math>\vec{\hat{F}} = \hat{F}_0\,(-\vec{\imath}_1 + \vec{\jmath}_1)</math>, con <math>\hat{F}_0>0</math>. Determina el movimiento de la varilla justo después de la percusión así como el valor de la percusión vincular en <math>A</math>.
| |
| #Discute el movimiento del punto <math>A</math> en función del valor de <math>s</math>. ¿Donde está el centro de percusión de <math>A</math>?
| |
|
| |
|
| = Solución = | | ==Solución== |
| | La masa realiza su movimiento circular como consecuencia de la acción de dos fuerzas: su peso y la tensión de la cuerda |
|
| |
|
| == Reducción cinemática ==
| | <center><math>m\vec{g}+\vec{F}_T = m\vec{a}</math></center> |
| La reducción cinemática en el punto <math>A</math> es
| |
| <center> | |
| <math> | |
| \vec{\omega}_{21} = \dot{\theta}\,\vec{k}_1, | |
| \qquad
| |
| \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1
| |
| </math> | |
| </center> | |
| El sólido tiene dos grados de libertad: <math>\{x,\theta\}</math>.
| |
|
| |
|
| == Energía cinética y potencial ==
| | <center>[[Archivo:masa-rotante-hilo.png]]</center> |
|
| |
|
| Calculamos la energía cinética pasando por el centro de masas del sólido
| | El peso va en la dirección vertical |
| <center>
| |
| <math>
| |
| T = T_{T} + T_{R}
| |
| </math>
| |
| </center>
| |
| La energía cinética de traslación es
| |
| <center>
| |
| <math>
| |
| T_{T} = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2
| |
| </math>
| |
| </center>
| |
| La velocidad del centro de masas es
| |
| <center>
| |
| <math>
| |
| \begin{array}{ll}
| |
| \vec{v}^{\,G}_{21}& = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG}
| |
| = -b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + (\dot{x} + b\dot{\theta}\cos\theta)\,\vec{\jmath}_1
| |
| \\
| |
| & \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1\\
| |
| & \vec{\omega}_{21}\times\overrightarrow{AG} = (\dot{\theta}\,\vec{k}_1)\times
| |
| (b\cos\theta\,\vec{\imath}_1 + b\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) =
| |
| -b\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + b\dot{\theta}\cos\theta\,\vec{\jmath}_1
| |
| \end{array}
| |
| </math>
| |
| </center>
| |
| Por tanto, la energía cinética de traslación es
| |
| <center>
| |
| <math>
| |
| T_T = \dfrac{1}{2}m\,(\dot{x}^2 + b^2\dot{\theta}^2 + 2b\dot{x}\dot{\theta}\cos\theta)
| |
| </math>
| |
| </center>
| |
| La energía cinética de rotación es
| |
| <center>
| |
| <math>
| |
| T_R = \dfrac{1}{2} I_G |\vec{\omega}_{21}|^2 = \dfrac{1}{2}\, \dfrac{1}{12}m(2b)^2\,\dot{\theta}^2
| |
| </math>
| |
| </center>
| |
| La energía cinética total es
| |
| <center>
| |
| <math>
| |
| T = \dfrac{1}{2}m\dot{x}^2 + \dfrac{2}{3}mb^2\dot{\theta}^2 + mb\dot{x}\dot{\theta}\cos\theta.
| |
| </math>
| |
| </center>
| |
|
| |
|
| La única fuerza conservartiva en el problema es la gravedad. Tomando como referencia de energía potencial gravitatoria la altura del punto <math>O</math> tenemos
| | <center><math>m\vec{g}=-mg\vec{k}</math></center> |
| <center> | |
| <math> | |
| U = U_g = -mgb\cos\theta.
| |
| </math> | |
| </center> | |
|
| |
|
| == Percusión ==
| | mientras que la tensión va en la dirección de la cuerda y por tanto tiene una componente radial hacia adentro y otra vertical hacia arriba. Si <math>\phi</math> es el ángulo que el hilo forma con la horizontal, la tensión se escribe |
|
| |
|
| La velocidad del punto <math>C</math> es
| | <center><math>\vec{F}_T = F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k}\right)</math></center> |
| <center> | |
| <math> | |
| \begin{array}{ll}
| |
| \vec{v}^{\,C}_{21}& = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AC} | |
| = -s\dot{\theta}\,\mathrm{sen}\,\theta + (\dot{x} + s\dot{\theta}\cos\theta)\,\vec{\jmath}_1
| |
| \\
| |
| & \vec{v}^{\,A}_{21} = \dot{x}\,\vec{\jmath}_1\\
| |
| & \vec{\omega}_{21}\times\overrightarrow{AC} = (\dot{\theta}\,\vec{k}_1)\times
| |
| (s\cos\theta\,\vec{\imath}_1 + s\,\mathrm{sen}\,\theta\,\vec{\jmath}_1) =
| |
| -s\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + s\dot{\theta}\cos\theta\,\vec{\jmath}_1
| |
| \end{array}
| |
| </math> | |
| </center> | |
|
| |
|
| La función de Lagrange es
| | Por último, la aceleración en un movimiento circular uniforme es puramente radial y hacia adentro, siendo su módulo proporcional al radio de la circunferencia y al cuadrado de la velocidad angular |
| <center>
| |
| <math>
| |
| L = T - U = \dfrac{1}{2}m\dot{x}^2 + \dfrac{2}{3}mb^2\dot{\theta}^2 + mb\dot{x}\dot{\theta}\cos\theta + mgb\cos\theta
| |
| </math>
| |
| </center>
| |
| Como hay dos grados de libertad, tendremos dos ecuaciones de Lagrange percusivas
| |
| <center>
| |
| <math>
| |
| \Delta p_x = \hat{Q}^{NC}_x,
| |
| \qquad
| |
| \Delta p_{\theta} = \hat{Q}^{NC}_{\theta}.
| |
| </math>
| |
| </center>
| |
| Para la primera tenemos
| |
| <center>
| |
| <math>
| |
| p_x = \dfrac{\partial L}{\partial \dot{x}} = m\dot{x} + mb\dot{\theta}\cos\theta
| |
| \Longrightarrow
| |
| \Delta p_x = \left.(m\Delta\dot{x} + mb\Delta\dot{\theta}\cos\theta)\right|_{x=0, \theta=0}
| |
| =
| |
| m\Delta\dot{x} + mb\Delta\dot{\theta}.
| |
| </math>
| |
| </center>
| |
| La percusión generalizada para la coordenada <math>x</math> es
| |
| <center>
| |
| <math>
| |
| \hat{Q}^{NC}_x = \vec{\hat{F}}\cdot\dfrac{\partial \vec{v}^{\,C}_{21}}{\partial\dot{x}}
| |
| = \left.\hat{F}_0\,(-\vec{\imath}_1+\vec{\jmath}_1)\cdot(\vec{\jmath}_1)\right|_{x=0, \theta=0}
| |
| =\hat{F}_0
| |
| </math>
| |
| </center>
| |
| Obtenemos así la ecuación
| |
| <center>
| |
| <math>
| |
| \Delta\dot{x} + b\Delta\dot{\theta} = \hat{F}_0/m\qquad (1)
| |
| </math>
| |
| </center>
| |
| Procedemos de manera similar para <math>\theta</math>
| |
| <center>
| |
| <math>
| |
| p_{\theta} = \dfrac{\partial L}{\partial \dot{\theta}} = \dfrac{4}{3}mb^2\dot{\theta} + mb\dot{x}\cos\theta
| |
| \Longrightarrow
| |
| \Delta p_{\theta} = \left.(\dfrac{4}{3}mb^2\Delta\dot{\theta} + mb\Delta\dot{x}\cos\theta)\right|_{x=0, \theta=0}
| |
| =
| |
| \dfrac{4}{3}mb^2\Delta\dot{\theta} + mb\Delta\dot{x}.
| |
| </math>
| |
| </center>
| |
| La percusión generalizada para la coordenada <math>\theta</math> es
| |
| <center>
| |
| <math>
| |
| \hat{Q}^{NC}_{\theta} = \vec{\hat{F}}\cdot\dfrac{\partial \vec{v}^{\,C}_{21}}{\partial\dot{\theta}}
| |
| = \left.\hat{F}_0\,(-\vec{\imath}_1+\vec{\jmath}_1)\cdot(-s\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + s\cos\theta\vec{\jmath}_1)\right|_{x=0, \theta=0}
| |
| =\hat{F}_0s
| |
| </math>
| |
| </center>
| |
| Obtenemos así la ecuación
| |
| <center>
| |
| <math>
| |
| 3\Delta\dot{x} + 4b\Delta\dot{\theta} = \dfrac{3\hat{F}_0s}{mb} \qquad (2)
| |
| </math>
| |
| </center>
| |
| Resolviendo para <math>\Delta\dot{x}</math> y <math>\Delta\dot{\theta}</math> obtenemos
| |
| <center>
| |
| <math>
| |
| \Delta\dot{x} = \dfrac{\hat{F}_0}{mb}\,(4b-3s),
| |
| \qquad
| |
| \Delta\dot{\theta} = -\dfrac{3\hat{F}_0}{mb^2}\,(b-s)
| |
| </math>
| |
| </center>
| |
| Como la barra parte del reposo: <math>\dot{x}^- = \dot{\theta}^-=0</math>. Por tanto
| |
| <center>
| |
| <math>
| |
| \dot{x}^+ = \dfrac{\hat{F}_0}{mb}\,(4b-3s),
| |
| \qquad
| |
| \dot{\theta}^+ = -\dfrac{3\hat{F}_0}{mb^2}\,(b-s)
| |
| </math>
| |
| </center>
| |
| [[File:MRGIC-PercusionSobreVarilla-Percusiones.png|right]]
| |
| La figura de la derecha muestra las percusiones que actúan sobre la barra, a saber, la percusión libre <math>\vec{\hat{F}}</math> y la percusión vincular <math>\vec{\hat{A}}</math>. Aplicando el T.C.M Percusivo tenemos
| |
| <center>
| |
| <math>
| |
| \Delta\vec{C} = \vec{\hat{F}} + \vec{\hat{A}}
| |
| \Longrightarrow
| |
| \vec{\hat{A}} = \Delta\vec{C} - \vec{\hat{F}}
| |
| </math>
| |
| </center>
| |
| La variación de la cantidad de movimiento es
| |
| <center>
| |
| <math>
| |
| \Delta\vec{C} = m\Delta\vec{v}^{\,G}_{21} =
| |
| \left.(-b\Delta\dot{\theta}\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + (\Delta\dot{x} + b\Delta\dot{\theta}\cos\theta)\,\vec{\jmath}_1)\right|_{x=0,\theta=0}
| |
| = (\Delta\dot{x} + b\Delta\dot{\theta})\,\vec{\jmath}_1.
| |
| </math>
| |
| </center>
| |
| Utilizando la solución calculada antes tenemos
| |
| <center>
| |
| <math>
| |
| \vec{\hat{A}} = \hat{F}_0\,\vec{\imath}_1
| |
| </math>
| |
| </center>
| |
|
| |
|
| == Movimiento de <math>A</math> en función de <math>s</math> ==
| | <center><math>m\vec{a}=-m\omega^2 R\vec{u}_\rho</math></center> |
| La velocidad de <math>A</math> justo después de la percusión es
| |
| <center> | |
| <math> | |
| \vec{v}^{\,A+}_{21} = \dot{x}^+\,\vec{\jmath}_1 = | |
| \dfrac{\hat{F}_0}{mb}\,(4b-3s)\,\vec{\jmath}_1 | |
| </math> | |
| </center> | |
| Vemos que si <math>s=s_p=4b/3</math> esta velocidad es nula. Ese valor de <math>s</math> indica la posición del centro de percusión de <math>A</math>. Si <math>s<s_p</math> (la parte de arriba de la barra) el punto <math>A</math> se mueve hacia la derecha. Si <math>s>s_p</math> (la parte de abajo de la barra) el punto <math>A</math> se mueve hacia la izquierda.
| |
|
| |
|
| [[Categoría:Problemas de examen de Mecánica Racional]]
| | aquí <math>R</math> no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud <math>b</math> de la cuerda por |
| [[Categoría:Problemas de Dinámica Impulsiva]]
| | |
| | <center><math>R = b\cos(\phi)\,</math></center> |
| | |
| | La velocidad angular la hallamos sabiendo que el enunciado nos da la frecuencia natural (2 vueltas por segundo, esto es 2 Hz). |
| | |
| | Sustituyendo todo esto en la ecuación de movimiento queda |
| | |
| | <center><math>-mg\vec{k}+F_T\left(-\cos(\phi)\vec{u}_\rho+\mathrm{sen}(\phi)\vec{k}\right)=-m\omega^2b\cos(\phi)\vec{u}_\rho</math></center> |
| | |
| | Igualando componente a componente |
| | |
| | <center><math>\left\{\begin{array}{rcl}-F_T\cos(\phi) & = & -m\omega^2b\cos(\phi) \\ && \\ -mg+F_T\mathrm{sen}(\phi) & = & 0\end{array}\right.</math></center> |
| | |
| | De la primera de estas dos obtenemos la tensión |
| | |
| | <center><math>F_T = m\omega^2 b\,</math></center> |
| | |
| | y, conocida la tensión, hallamos el ángulo con la horizontal |
| | |
| | <center><math>\mathrm{sen}(\phi) = \frac{mg}{F_T}=\frac{g}{\omega^2b}</math></center> |
| | |
| | Vemos que el ángulo es independiente de la masa de la bola, y que existe un valor inferior para la velocidad angular, ya que si es demasiado baja implicaría un seno mayor que la unidad, lo que no es posible. |
| | |
| | Sustituyendo los valores del enunciado obtenemos el valor numérico de la velocidad angular |
| | |
| | <center><math>\omega = 2\pi f = 4\pi\,\frac{\mathrm{rad}}{\mathrm{s}}</math></center> |
| | |
| | la tensión |
| | |
| | <center><math>F_T = (0.5\,\mathrm{kg})\left(4\pi\,\frac{\mathrm{rad}}{\mathrm{s}}\right)^2(0.5\,\mathrm{m})=39.5\,\mathrm{N}</math></center> |
| | |
| | y el ángulo con la horizontal. |
| | |
| | <center><math>\mathrm{sen}(\phi) = \frac{9.81\,\mathrm{m}/\mathrm{s}^2}{(4\pi \mathrm{s}^{-1})^2(0.5\,\mathrm{m})} = 0.124\qquad\Rightarrow\qquad \phi = 0.124\,\mathrm{rad}=7.13^\circ</math></center> |
Enunciado
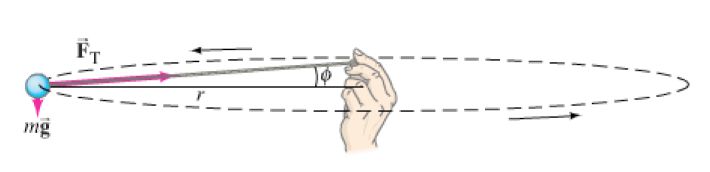
Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal.
Solución
La masa realiza su movimiento circular como consecuencia de la acción de dos fuerzas: su peso y la tensión de la cuerda

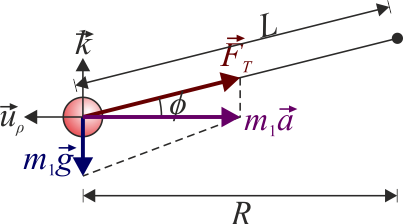
El peso va en la dirección vertical

mientras que la tensión va en la dirección de la cuerda y por tanto tiene una componente radial hacia adentro y otra vertical hacia arriba. Si  es el ángulo que el hilo forma con la horizontal, la tensión se escribe
es el ángulo que el hilo forma con la horizontal, la tensión se escribe

Por último, la aceleración en un movimiento circular uniforme es puramente radial y hacia adentro, siendo su módulo proporcional al radio de la circunferencia y al cuadrado de la velocidad angular

aquí  no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud
no es la longitud de la cuerda, sino el radio de la circunferencia. Este se relaciona con la longitud  de la cuerda por
de la cuerda por

La velocidad angular la hallamos sabiendo que el enunciado nos da la frecuencia natural (2 vueltas por segundo, esto es 2 Hz).
Sustituyendo todo esto en la ecuación de movimiento queda

Igualando componente a componente

De la primera de estas dos obtenemos la tensión

y, conocida la tensión, hallamos el ángulo con la horizontal

Vemos que el ángulo es independiente de la masa de la bola, y que existe un valor inferior para la velocidad angular, ya que si es demasiado baja implicaría un seno mayor que la unidad, lo que no es posible.
Sustituyendo los valores del enunciado obtenemos el valor numérico de la velocidad angular

la tensión

y el ángulo con la horizontal.

















