Diferencia entre las páginas «Barra deslizando en cuenco semiesférico, Enero 2021 (G.I.E.R.M.)» y «Masa con cuerda desenrollándose de un disco, Enero 2021 (G.I.E.R.M.)»
(Página creada con «= Enunciado = right Una barra de longitud <math>L</math> (sólido "2") desliza en un cuenco de radio <math>R</math> (sólido "1"). El punto <math>A</math> de la barra desliza sobre la circunferencia del cuenco y el punto de la barra que en cada instante está en contacto con la esquina (punto <math>C</math> en la figura) desliza sobre esa esquina. En el instante indicado en la figura el punto <math>A</math> de la barra es…») |
(Página creada con «= Enunciado = right Una masa <math>m</math> desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante elástica <math>k=mg/R</math> y longitud natural <math>l_0=R</math>. Por el otro lado tira de ella una cuerda sin masa que puede enrollarse y desenrollarse en un disco de masa <math>m</math> y radio <math>R</math>. El disco puede rotar alrededor de un eje perpendicular a él que pasa por…») |
||
| Línea 1: | Línea 1: | ||
= Enunciado = | = Enunciado = | ||
[[Archivo:F1GIERM- | [[Archivo:F1GIERM-masaMuelleDisco-enunciado.png|right]] | ||
Una | Una masa <math>m</math> desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante | ||
elástica <math>k=mg/R</math> y longitud natural <math>l_0=R</math>. Por el otro lado tira de ella una cuerda sin masa que | |||
puede enrollarse y desenrollarse en un disco de masa <math>m</math> y radio <math>R</math>. El disco puede rotar alrededor de | |||
el punto <math> | un eje perpendicular a él que pasa por su centro. El sistema está sometido a la | ||
acción de la gravedad. En el instante inicial la masa se encuentra en el punto <math>B</math>. Tanto la masa como | |||
# | el disco están en reposo en ese instante inicial. Durante todo el movimiento la cuerda permanece tensa. | ||
# | El momento de inercia de un disco de masa <math>M</math> y radio <math>R</math> | ||
# | respecto a un eje perpendicular a él que pasa por su centro es <math>I=MR^2/2</math>. | ||
#Calcula la rapidez de la masa cuando llega al punto <math>O</math> | |||
#¿Qué trabajo ha hecho la cuerda sobre la masa durante su movimiento? | |||
#Si el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico <math>\mu</math>, calcula la velocidad de la masa en el punto <math>O</math> | |||
#¿Qué condición debe cumplir <math>\mu</math> para que la masa no llegue al punto <math>O</math>? | |||
= Solución = | = Solución = | ||
''' | ''' Velocidad de la masa en <math>O</math> (sin rozamiento) ''' | ||
[[Archivo:F1GIERM- | |||
[[Archivo:F1GIERM-masaMuelleDisco-fuerzas.png|right|450px]] | |||
La figura de la derecha muestra las | La figura de la derecha muestra las fuerzas que actúan sobre la masa y el disco en la situación sin rozamiento. El peso y la fuerza elástica del muelle son conservativas. La fuerza normal sobre la masa no hace trabajo, pues es siempre perpendicular a su velocidad. La fuerza vincular sobre el centro del disco no hace trabajo pues ese punto no se mueve. | ||
Por otro lado, la cuerda si hace trabajo sobre la masa y el punto <math>A</math> del disco, pues la potencia que transmite a la masa y al disco es | |||
<center> | |||
<math> | |||
\vec{T}_m\cdot\vec{v}_m\neq 0, \qquad \vec{T}_A\cdot\vec{v}_A\neq0. | |||
</math> | |||
</center> | |||
Estas fuerzas no son conservativas. Sin embargo, el trabajo total es cero. En efecto, puesto que <math>\vec{v}_m = \vec{v}_A</math> y también <math>\vec{T}_m = -\vec{T}_A</math> (la cuerda no tiene masa), se cumple | |||
<center> | |||
<math> | |||
\vec{T}_m\cdot\vec{v}_m + \vec{T}_A\cdot\vec{v}_A | |||
= | |||
(\vec{T}_m + \vec{T}_A)\cdot\vec{v}_m = 0. | |||
</math> | |||
</center> | |||
Por tanto, la energía mecánica del sistema se conserva. | |||
Tanto la masa como el disco tienen energía cinética. Sus valores son | |||
<center> | |||
<math> | |||
\begin{array}{l} | |||
T_m = \dfrac{1}{2}mv_m^2,\\ | |||
\\ | |||
T_d = \dfrac{1}{2}m v_C^2 + \dfrac{1}{2}I w^2 = 0 + \dfrac{1}{2}I\,\dfrac{v_A^2}{R^2} | |||
= | |||
\dfrac{1}{4}mv_m^2. | |||
\end{array} | |||
</math> | |||
</center> | |||
Hemos usado el valor del momento de inercia que proporciona el enunciado y el hecho de que en el punto <math>A</math> del disco se cumple <math>v_A = wR</math>. Por tanto, la energía cinética total es | |||
<center> | |||
<math> | |||
T = T_m + T_d = \dfrac{3}{4}mv_m^2. | |||
</math> | |||
</center> | |||
La energía potencial elástica asociada al muelle es | |||
<center> | <center> | ||
<math> | <math> | ||
\ | U_k = \dfrac{1}{2}k\,(s-l_0)^2 = \dfrac{1}{2}\dfrac{mg}{R}(s-R)^2 | ||
= | |||
\dfrac{1}{2}mgR\,\left(\dfrac{s}{R}-1\right)^2. | |||
</math> | </math> | ||
</center> | </center> | ||
La energía potencial gravitatoria es constante durante todo el movimiento, pues las alturas de la masa y del centro del disco no cambian. Por tanto no hace falta tenerla en cuenta, pues al igualar las energías mecánicas se va a cancelar. | |||
En el instante inicial tenemos | |||
<center> | |||
<math> | |||
v_m = 0, \quad s=3R | |||
\Longrightarrow | |||
E_i = 2mgR. | |||
</math> | |||
</center> | |||
Cuando la masa llegue a <math>O</math> se tiene | |||
<center> | |||
<math> | |||
v_m = v_O, \quad s=0 | |||
\Longrightarrow | |||
E_f = \dfrac{3}{4}mv_O^2 + \dfrac{1}{2}mgR. | |||
</math> | |||
</center> | |||
Entnonces | |||
<center> | |||
<math> | |||
E_i = E_f | |||
\Longrightarrow | |||
v_O = \sqrt{2gR}. | |||
</math> | |||
</center> | |||
''' | ''' Trabajo de la cuerda sobre la masa ''' | ||
La fuerza ejercida por la cuerda es no conservativa. Es la única fuerza no conservativa que actúa sobre la masa y que realiza trabajo. Entonces, la variación de '''energía mecánica de la masa''' es el trabajo realizado por esa fuerza | |||
<center> | <center> | ||
<math> | <math> | ||
W_c = \Delta E^{masa} | |||
</math> | </math> | ||
</center> | </center> | ||
Tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
\ | \begin{array}{l} | ||
E^{masa}_i = \dfrac{1}{2}k(3R-R)^2 = 2mgR,\\ | |||
\\ | |||
E^{masa}_f = \dfrac{1}{2}mv_O^2 + \dfrac{1}{2}k(0-R)^2 = mgR + \dfrac{1}{2}mgR | |||
= | = | ||
\ | \dfrac{3}{2}mgR. | ||
\end{array} | |||
</math> | </math> | ||
</center> | </center> | ||
Por | Por tanto | ||
<center> | <center> | ||
<math> | <math> | ||
W_c = E^{masa}_f - E^{masa}_i = -\dfrac{1}{2}mgR. | |||
</math> | </math> | ||
</center> | </center> | ||
Este trabajo es negativo, pues la cuerda tira de la masa hacia la derecha mientras que la masa se desplaza hacia la izquierda. | |||
''' Velocidad | ''' Velocidad de la masa con rozamiento ''' | ||
[[Archivo:F1GIERM-masaMuelleDisco-fuerzasRozamiento.png|right|450px]] | |||
Si hay rozamiento sobre la masa la energía mecánica no se conserva. Sin embargo, podemos calcular el trabajo realizado por la fuerza de rozamiento. Como estamos en régimen dinámico, la fuerza de rozamiento es constante y la masa hace un movimiento rectilíneo, tenemos | |||
<center> | <center> | ||
<math> | <math> | ||
W_R = \vec{F}_R\cdot\overrightarrow{BO} | |||
= | = | ||
(\mu mg\,\vec{\imath})\cdot(-3R\,\vec{\imath}) = -3\mu mgR. | |||
</math> | |||
</center> | |||
El balance de energía mecánica es | |||
<center> | |||
<math> | |||
\Delta E = E_f - E_i = W_R | |||
\Longrightarrow | |||
\dfrac{3}{4}mv_O^2 + \dfrac{1}{2}mgR - 2mgR = -3\mu mgR | |||
\Longrightarrow | |||
v_O = \sqrt{2gR\,(1-2\mu)}. | |||
</math> | </math> | ||
</center> | </center> | ||
''' Condición para que la masa no llegue a <math>O</math> ''' | |||
Para que no llegue la masa el radicando del valor de <math>v_O</math> obtenido en el apartado anterior debe ser negativo | |||
<center> | |||
<math> | |||
1-2\mu < 0 | |||
\Longrightarrow | |||
\mu > 1/2. | |||
</math> | |||
</center> | |||
[[Categoría: Problemas de | [[Categoría:Problemas de dinámica de un sistema de partículas]] | ||
[[Categoría:Problemas de examen]] | |||
[[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]] | [[Categoría:Problemas de Examen de Física I (G.I.E.R.M.)]] | ||
Revisión actual - 14:47 31 oct 2023
Enunciado

Una masa desliza sobre una superficie horizontal lisa. Está conectada a un muelle de constante elástica y longitud natural . Por el otro lado tira de ella una cuerda sin masa que puede enrollarse y desenrollarse en un disco de masa y radio . El disco puede rotar alrededor de un eje perpendicular a él que pasa por su centro. El sistema está sometido a la acción de la gravedad. En el instante inicial la masa se encuentra en el punto . Tanto la masa como el disco están en reposo en ese instante inicial. Durante todo el movimiento la cuerda permanece tensa. El momento de inercia de un disco de masa y radio respecto a un eje perpendicular a él que pasa por su centro es .
- Calcula la rapidez de la masa cuando llega al punto
- ¿Qué trabajo ha hecho la cuerda sobre la masa durante su movimiento?
- Si el contacto entre la masa y la superficie horizontal es rugoso con coeficiente de rozamiento dinámico , calcula la velocidad de la masa en el punto
- ¿Qué condición debe cumplir para que la masa no llegue al punto ?
Solución
Velocidad de la masa en (sin rozamiento)
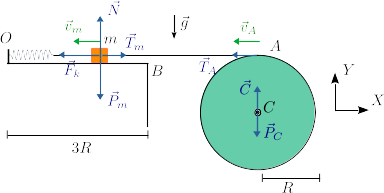
La figura de la derecha muestra las fuerzas que actúan sobre la masa y el disco en la situación sin rozamiento. El peso y la fuerza elástica del muelle son conservativas. La fuerza normal sobre la masa no hace trabajo, pues es siempre perpendicular a su velocidad. La fuerza vincular sobre el centro del disco no hace trabajo pues ese punto no se mueve.
Por otro lado, la cuerda si hace trabajo sobre la masa y el punto del disco, pues la potencia que transmite a la masa y al disco es
Estas fuerzas no son conservativas. Sin embargo, el trabajo total es cero. En efecto, puesto que y también (la cuerda no tiene masa), se cumple
Por tanto, la energía mecánica del sistema se conserva.
Tanto la masa como el disco tienen energía cinética. Sus valores son
Hemos usado el valor del momento de inercia que proporciona el enunciado y el hecho de que en el punto del disco se cumple . Por tanto, la energía cinética total es
La energía potencial elástica asociada al muelle es
La energía potencial gravitatoria es constante durante todo el movimiento, pues las alturas de la masa y del centro del disco no cambian. Por tanto no hace falta tenerla en cuenta, pues al igualar las energías mecánicas se va a cancelar.
En el instante inicial tenemos
Cuando la masa llegue a se tiene
Entnonces
Trabajo de la cuerda sobre la masa
La fuerza ejercida por la cuerda es no conservativa. Es la única fuerza no conservativa que actúa sobre la masa y que realiza trabajo. Entonces, la variación de energía mecánica de la masa es el trabajo realizado por esa fuerza
Tenemos
Por tanto
Este trabajo es negativo, pues la cuerda tira de la masa hacia la derecha mientras que la masa se desplaza hacia la izquierda.
Velocidad de la masa con rozamiento
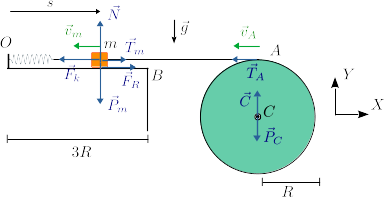
Si hay rozamiento sobre la masa la energía mecánica no se conserva. Sin embargo, podemos calcular el trabajo realizado por la fuerza de rozamiento. Como estamos en régimen dinámico, la fuerza de rozamiento es constante y la masa hace un movimiento rectilíneo, tenemos
El balance de energía mecánica es
Condición para que la masa no llegue a
Para que no llegue la masa el radicando del valor de obtenido en el apartado anterior debe ser negativo



























