Termómetro con dos cámaras de gas

Enunciado

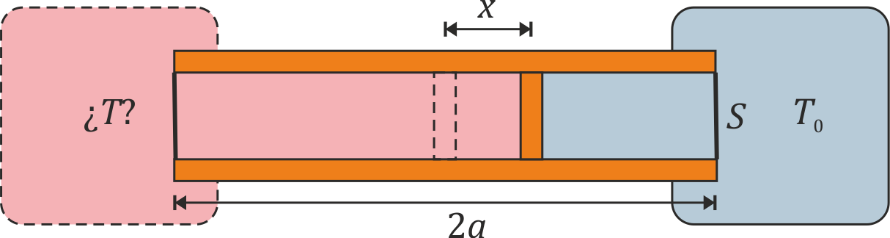
Se construye un termómetro de gas ideal según el siguiente principio: un tubo cilíndrico de sección $A$ y longitud $2a$ con paredes adiabáticas y bases diatermas es dividido por un pistón, también adiabático, que puede deslizarse sin rozamiento por el interior del tubo. En el interior de las dos cámaras se encuentra un gas ideal. Una de las dos cámaras se mantiene en contacto térmico con un foco a temperatura $T_{0}$ , mientras que la otra se pone en contacto con el sistema cuya temperatura se quiere medir. Cuando las dos temperaturas son iguales el pistón se encuentra en la posición central y la presión del gas es $p_{0}$ .

Calcule la temperatura absoluta $T$ a la que se encuentra el sistema cuando el pistón se ha desplazado una cantidad $x$ desde el centro hacia el sistema a $T_{0}$ . ¿Resulta una escala lineal de temperaturas? ¿A cuánto tiende $x$ si $T\to 0$ o si $T\to \infty$ ?
Supongamos que el tubo mide 20 cm, la temperatura de referencia es $T_{0}=300\,\mathrm {K}$ y el pistón se desplaza 1 cm. ¿Cuál es la temperatura del sistema exterior?

Escala de temperaturas

Nuestro sistema es el cilindro con las dos cámaras. Este sistema intercambia calor de dos modos. La cámara derecha cede o absorbe calor del foco a temperatura constante $T_{0}$ , de modo que la temperatura de esta cámara es siempre $T_{0}$ . La cámara de la izquierda intercambia calor con el sistema del que se quiere medir la temperatura. Es decir, ninguna de las dos cámaras es adiabática. Los procesos en la cámara de la derecha son isotermos, mientras que los de la izquierda no mantienen ninguna magnitud termodinámica constante.

Para medir la temperatura de un sistema ponemos en contacto la cámara izquierda con él. El trasvase de calor que se produce hace que varíe el estado del gas en esta cámara, por lo que se altera el valor de la presión. Entonces, el pistón se desplaza, con lo cual cambia el volumen de los dos gases. El equilibrio se recupera cuando la presión a ambos lados del pistón sea la misma. Los dos gases tendrán en general temperaturas distintas pues el pistón es adiabático y no permite el paso de calor.

Cuando las temperaturas son iguales en ambas cámaras el pistón está en el centro del cilindro y el volumen ocupado por los dos gases es el mismo

V_{L0}=V_{R0}=Sa\,

Si el pistón se desplaza hacia la derecha, el volumen de la cámara izquierda aumenta y el de la derecha disminuye

{\begin{array}{l}V_{L}=S(a+x)\\\\V_{R}=S(a-x)\end{array}}

Cuando el pistón se desplaza hacia la izquierda los valores de $x$ son negativos, con lo que estas expresiones también dan el valor correcto del volumen ocupado por cada gas.

Al poner en contacto el gas de la izquierda con el sistema a temperatura $T$ el nuevo equilibrio se alcanza cuando las presiones en los dos gases son iguales. En ese instante, para la cámara de la izquierda

{\frac {p_{0}Sa}{T_{0}}}={\frac {p_{L0}V_{L0}}{T_{L0}}}={\frac {p_{L}V_{L}}{T_{L}}}={\frac {pS(a+x)}{T}}

y para la de la derecha

{\frac {p_{0}Sa}{T_{0}}}={\frac {p_{L0}V_{L0}}{T_{L0}}}={\frac {p_{L}V_{L}}{T_{L}}}={\frac {pS(a-x)}{T_{0}}}

Igualando ambas cantidades obtenemos

\frac{a+x}{T}=\frac{a-x}{T_0} \qquad\Rightarrow\qquad T = T_0\,\frac{a+x}{a-x}

Está función no es lineal, pues su gráfica no corresponde a una línea recta.

Para examinar los límites propuestos en el enunciado despejamos $x$ en función de $T$

\displaystyle x={\frac {T-T_{0}}{T+T_{0}}}a

Cuando $T\to 0$ obtenemos $x\to -a$ . Si el sistema exterior está muy frío el pistón tiende a situarse en el extremo izquierdo. En el otro límite, si $T\to \infty$ se tiene $x\to +a$ . Si el sistema está muy caliente el pistón se desplaza hacia la derecha.