Enunciado
Considere la terna de vectores
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1 = \cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath} \qquad \vec{u}_2 = -\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath} \qquad \vec{u}_3 = \vec{k} }
- Pruebe que constituyen una base ortonormal dextrógira. ¿Cómo están situados estos vectores?
- Halle la transformación inversa, es decir, exprese Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\imath},\vec{\jmath},\vec{k}\}}
como combinación de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_1,\vec{u}_2,\vec{u}_3\}}
.
- Para el caso particular en que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(\theta) = 3/4}
, particularice las ecuaciones de transformación y exprese el vector Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=10\vec{\imath}-15\vec{\jmath}+3\vec{k}}
en la nueva base.
Base ortonormal dextrógira
Base ortonormal
Para demostrar que se tra de una base ortonormal hay que probar que son unitarios y ortogonales entre sí, es decir
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_i\cdot\vec{u}_k=\begin{cases}1 & i = k \\ 0 & i\neq k\end{cases}}
Calculamos entonces los productos escalares:
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1}
consigo mismo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1\cdot\vec{u}_1=\cos^2(\theta)+\mathrm{sen}^2(\theta) = 1}
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1}
con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2}
(y viceversa, por la conmutatividad)
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1\cdot\vec{u}_2=\vec{u}_2\cdot\vec{u}_1=\cos(\theta)(-\mathrm{sen}(\theta))+\mathrm{sen}(\theta)\cos(\theta) = 0}
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1}
con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3}
(y viceversa). Es fácil ver que son ortogonales ya que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1}
no tiene componente en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{k}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_1=(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})\cdot\vec{k}= \cos(\theta)\overbrace{\vec{\imath}\cdot\vec{k}}^{=0}+\mathrm{sen}(\theta)\overbrace{\vec{\jmath}\cdot\vec{k}}^{=0} = 0}
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2}
consigo mismo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2\cdot\vec{u}_2=(-\mathrm{sen}(\theta))^2+\cos^2(\theta) = 1}
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2}
con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3}
(y viceversa). Se anula el producto escalar por la misma razón que el de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1}
con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2\cdot\vec{u}_3=\vec{u}_3\cdot\vec{u}_1=(-\mathrm{sen}(\theta)\vec{\imath}+\cos(\theta)\vec{\jmath})\cdot\vec{k}= -\mathrm{sen}(\theta)\overbrace{\vec{\imath}\cdot\vec{k}}^{=0}+\cos(\theta)\overbrace{\vec{\jmath}\cdot\vec{k}}^{=0} = 0}
- De Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3}
consigo mismo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3\cdot\vec{u}_3=\vec{k}\cdot\vec{k} = 1}
Por tanto, hemos demostrado que la relación anterior para los productos escalares se cumple y la base es ortonormal.
Base dextrogira
Para demostrar que se trata de una base dextrógira hemos de probar que se cumple la regla de la mano derecha, es decir, que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1\times\vec{u}_2=\vec{u}_3\qquad \qquad \vec{u}_2\times\vec{u}_3=\vec{u}_1\qquad \qquad \vec{u}_3\times\vec{u}_1=\vec{u}_2}
Probamos la primera de las igualdades
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1\times\vec{u}_2=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \cos(\theta) & \mathrm{sen}(\theta) & 0 \\ -\mathrm{sen}(\theta) & \cos(\theta) & 0\end{matrix}\right|=(\cos^2(\theta)+\mathrm{sen}^2(\theta))\vec{k}=\vec{k}}
De la misma manera se demuestran las otras dos igualdades. Una forma alternativa de demostrarlas es observar que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2\times\vec{u}_3 = \vec{u}_2\times(\vec{u}_1\times\vec{u}_2)}
Aplicamos las propiedades del doble producto vectorial
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_2\times\vec{u}_3 = \overbrace{(\vec{u}_2\cdot \vec{u}_2)}^{=1}\vec{u}_1-\overbrace{(\vec{u}_2\cdot \vec{u}_1)}^{=0}\vec{u}_2=\vec{u}_1}
y de la misma manera se obtiene la tercera
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_3\times\vec{u}_1=\vec{u}_2}
por lo que la base es ortonormal y dextrógira.
Esta base supone una rotación de un ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \theta}
alrededor del eje OZ.
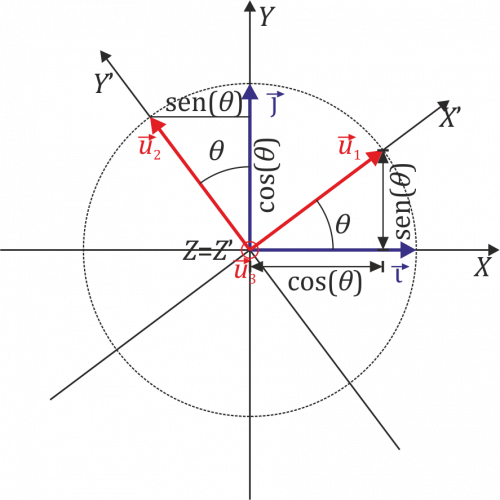
Transformación inversa
La transformación inversa consiste en escribir la base canónica Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{\imath},\vec{\jmath},\vec{k}\}}
como combinación lineal de la base Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \{\vec{u}_1,\vec{u}_2,\vec{u}_3\}}
, es decir, escribir Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}}
en la forma
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}=(\ldots)\vec{u}_1 + (\ldots)\vec{u}_2+ (\ldots)\vec{u}_3}
para ello, aplicamos que las componentes de un vector en una base ortonormal se obtienen proyectando sobre cada vector de esa base
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=F_1\vec{u}_1+F_2\vec{u}_2+F_3\vec{u}_3\qquad\Rightarrow\qquad F_k=\vec{F}\cdot\vec{u}_k}
y que el producto escalar es independiente de la base que se emplee para calcularlo. En particular podemos emplear la propia base canónica. En ese caso las componentes de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}}
serán
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} i_1=\vec{\imath}\cdot\vec{u}_1 & = & \vec{\imath}\cdot(\cos(\theta)\vec{\imath}+\mathrm{sen}(\theta)\vec{\jmath})= \cos(\theta) \\ i_1=\vec{\imath}\cdot\vec{u}_2 & = & \vec{\imath}\cdot(-\mathrm{sen}(\theta)\vec{\imath}+\mathrm{cos}(\theta)\vec{\jmath})= -\mathrm{sen}(\theta) \\ i_1=\vec{\imath}\cdot\vec{u}_3 & = & \vec{\imath}\cdot\vec{k}=0 \end{array}}
y por tanto
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\imath}=\cos(\theta)\vec{u}_1-\mathrm{sen}(\theta)\vec{u}_2}
De la misma manera obtenemos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\jmath}=\mathrm{sen}(\theta)\vec{u}_1+\mathrm{cos}(\theta)\vec{u}_2}
y, trivialmente,
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{k}=\vec{u}_3}
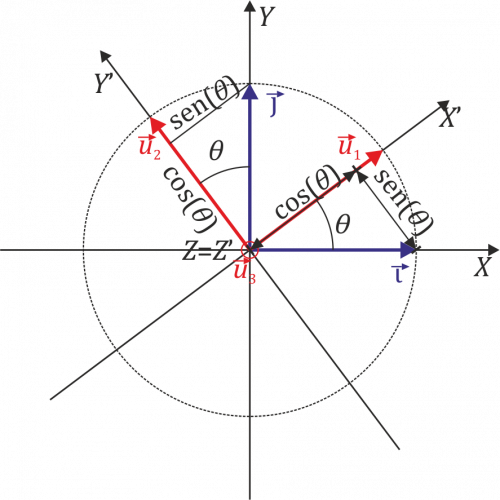
Gráficamente, lo que hacemos ahora es proyectar ortogonalmente la antigua base sobre la nueva.
Caso particular
En el caso particular Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(\theta) = 0.75 = 3/4}
el seno y el coseno valen
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(\theta)=\frac{4}{\sqrt{4^2+3^2}}=\frac{4}{5}=0.8\qquad\qquad\mathrm{sen}(\theta)=\frac{3}{\sqrt{4^2+3^2}}=\frac{3}{5}=0.6}
con lo que la relación entre las bases se particulariza a
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{u}_1 = \frac{4}{5}\vec{\imath}+\frac{3}{5}\vec{\jmath} \qquad \vec{u}_2 = -\frac{3}{5}\vec{\imath}+\frac{4}{5}\vec{\jmath} \qquad \vec{u}_3 = \vec{k} }
Para hallar las componentes de
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=10\vec{\imath}-15\vec{\jmath}+3\vec{k}}
aplicamos de nuevo que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=F_1\vec{u}_1+F_2\vec{u}_2+F_3\vec{u}_3\qquad\Rightarrow\qquad F_k=\vec{F}\cdot\vec{u}_k}
lo que nos da
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl} F_1=\vec{F}\cdot\vec{u}_1 & = & \left(10\vec{\imath}-15\vec{\jmath}+3\vec{k}\right)\cdot\left(\dfrac{4}{5}\vec{\imath}+\dfrac{3}{5}\vec{\jmath}\right)= \dfrac{10\times 4-15\times 3}{5}=-1 \\ && \\ F_2=\vec{F}\cdot\vec{u}_2 & = & \left(10\vec{\imath}-15\vec{\jmath}+3\vec{k}\right)\cdot\left(-\dfrac{3}{5}\vec{\imath}+\dfrac{4}{5}\vec{\jmath}\right)= \dfrac{-10\times 3-15\times 4}{5}=-18 \\ && \\ F_1=\vec{F}\cdot\vec{u}_3 & = & \left(10\vec{\imath}-15\vec{\jmath}+3\vec{k}\right)\cdot\left(\vec{k}\right)= 3 \end{array}}
y por tanto la expresión de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}}
en esta base es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{F}=-\vec{u}_1-18\vec{u}_2+3\vec{u}_3}
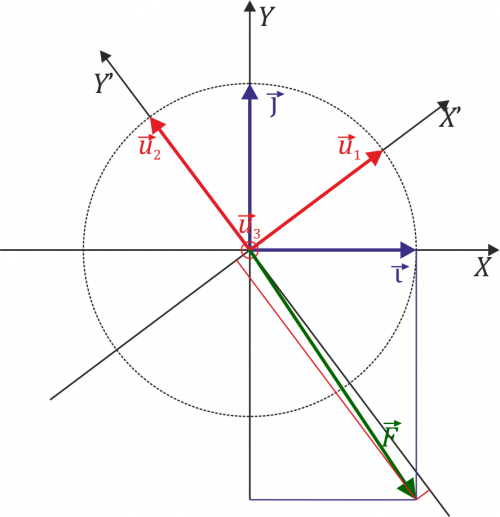
Hay que destacar que aunque las componentes cambien, el vector en sí no se ha visto modificado.
Podemos ver que el módulo del vector no se ve afectado porque usemos una base u otra
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt{10^2+15^2+3^2} = \sqrt{334}\qquad\qquad\sqrt{1^2+18^2+3^2}=\sqrt{334}}


