Primera Prueba de Control 2016/17 (G.I.C.)

Partícula moviéndose sobre una parábola

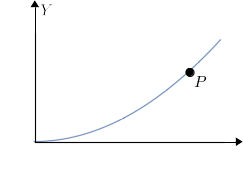
Una partícula recorre una parábola de ecuación $y=x^{2}/k$, siendo $k$ una constante. La partícula se mueve de modo que la velocidad sobre el eje $OX$ es constante e igual a $v_{0}$. En el instante inicial la partícula se encontraba en el origen de coordenadas.

1. Determina las unidades base de $k$ en el S.I.
2. Calcula el vector de posición de la partícula.
3. Determina la aceleración de la partícula.
4. Calcula el vector aceleración normal en el instante de tiempo $t_{0}=k/v_{0}$.
5. En ese mismo instante, calcula el valor del radio de curvatura.

Partícula con movimiento unidimensional

Una partícula realiza un movimiento unidimensional de modo que, en todo instante, su velocidad es $v=A/x$, siendo $A$ una constante y $x$ la coordenada de la partícula sobre el eje $OX$. En el instante inicial se tiene $x(0)=x_{0}$. Calcula su velocidad y su posición en función del tiempo.

Partícula en semiaro con muelle anclado en un extremo

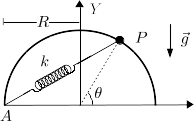
Una partícula de masa $m$ está engarzada en un semiaro de radio $R$ cuyo centro coincide con el origen de coordenadas, como se observa en la figura. La partícula está conectada a un muelle de constante elástica $k$ y longitud natural nula conectada al punto $A$. La gravedad actúa hacia abajo.

1. Dibuja el diagrama de cuerpo libre de la partícula en situación de contacto rugoso, indicando de que fuerzas se conoce su dirección y sentido y de cuales no.
2. Escribe la expresión que da la fuerza que el muelle ejerce sobre la partícula.
3. En situación de contacto liso, encuentra el valor del ángulo de equilibrio.
4. Supongamos ahora que el contacto es rugoso con un coeficiente de rozamiento estático $\mu$. Además el ángulo $\theta$ es tal que $\cos \theta =3/5$, y el sistema se ajusta de modo que $mg=kR$. ¿Cuál es valor mínimo del coeficiente de rozamiento para que esta configuración sea de equilibrio?