Barra deslizando en cuenco semiesférico, Enero 2021 (G.I.E.R.M.)

Enunciado

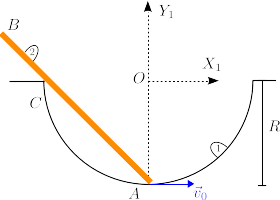
Una barra de longitud $L$ (sólido "2") desliza en un cuenco de radio $R$ (sólido "1"). El punto $A$ de la barra desliza sobre la circunferencia del cuenco y el punto de la barra que en cada instante está en contacto con la esquina (punto $C$ en la figura) desliza sobre esa esquina. En el instante indicado en la figura el punto $A$ de la barra está en el punto mas bajo del cuenco. El punto $A$ realiza un movimiento circular uniforme sobre el cuenco con rapidez constante $v_{0}$. Calcula las siguientes magnitudes

1. La posición del C.I.R. del movimiento {21}.
2. El vector rotación de ese movimiento.
3. La velocidad ${\vec {v}}_{21}^{\,O}$.

Solución

Posición del C.I.R.

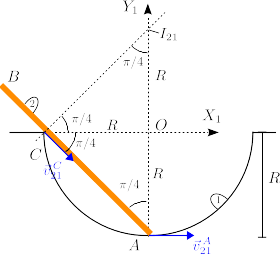
La barra realiza un movimiento plano. La figura de la derecha muestra las direcciones de las velocidades del movimiento en los puntos $A$ y $C$. Trazando por esos puntos sendas rectas perpendiculares a las velocidades, su punto de corte indica la posición del C.I.R. del movimiento {21}. Todos los ángulos indicados son de $\pi /4$. Por tanto

${\overrightarrow {OI}}_{21}=R\,{\vec {\jmath }}_{1}.$

Vector rotación

Al ser un movimiento se cumple

${\vec {\omega }}_{21}=\omega \,{\vec {k}}.$

Aplicamos el Teorema de Chasles entre los puntos $I_{21}$ y $A$:

${\vec {v}}_{21}^{\,A}={\vec {v}}_{21}^{I_{21}}+{\vec {\omega }}_{21}\times {\overrightarrow {I_{21}A}}={\vec {0}}+(\omega \,{\vec {k}})\times (-2R\,{\vec {\jmath }}_{1})=2\omega R\,{\vec {\imath }}_{1}.$

Por otro lado del enunciado sabemos que ${\vec {v}}_{21}^{\,A}=v_{0}\,{\vec {\imath }}_{1}$. Igualando llegamos a

${\vec {\omega }}_{21}={\dfrac {v_{0}}{2R}}\,{\vec {k}}.$

Velocidad del punto $O$

El hecho de que el punto $O$ coincida con el origen no implica que su velocidad sea cero. En este caso no lo es. Aplicamos Chasles entre el C.I.R. y el punto $O$

${\vec {v}}_{21}^{\,O}={\vec {v}}_{21}^{I_{21}}+{\vec {\omega }}_{21}\times {\overrightarrow {I_{21}O}}={\vec {0}}+\left({\dfrac {v_{0}}{2R}}\,{\vec {k}}\right)\times (-R\,{\vec {\jmath }}_{1})={\dfrac {v_{0}}{2}}\,{\vec {\imath }}_{1}.$

Hay que recordar que en el punto geométrico $O$ coinciden dos puntos distintos: uno que se mueve con la barra (perteneciente al sólido "2") y otro que se queda quieto (perteneciente al sólido "1"). Es la velocidad del primero de estos puntos la que se pide.