Campo de dos planos paralelos (GIOI)

Enunciado

Suponga que se tienen dos planos infinitos paralelos separados una distancia b que almacenan respectivamente densidades de carga $+\sigma _{0}$ y $-\sigma _{0}$. Calcule el campo eléctrico en todos los puntos del espacio.

Solución

Este problema puede resolverse por simple superposición de los campos de los planos individuales.

Según se ve en el problema “Campo de un plano infinito”, el campo debido a un plano cargado con una densidad superficial de carga uniforme $\sigma _{0}$

${\vec {E}}={\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {n}}$

donde ${\vec {n}}$ s el ector normal exterior al plano (que apunta en la dirección que se aleja de él).

Si tenemos dos planos, situados en $x=0$ y $x=b$, el primero con densidad de carga $+\sigma _{0}$ y el segundo con $-\sigma _{0}$, el espacio se divide en tres zonas.

En x < 0

En esta región, el vector normal exterior de ambos planos es $-{\vec {\imath }}$ por lo que el campo en esta región vale

${\vec {E}}={\vec {E}}_{1}+{\vec {E}}_{2}={\frac {\sigma _{0}}{2\varepsilon _{0}}}(-{\vec {\imath }})+{\frac {(-\sigma _{0})}{2\varepsilon _{0}}}(-{\vec {\imath }})=-{\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}+{\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}={\vec {0}}$

Vemos que los dos campos son del mismo módulo y dirección, pero sentidos opuestos, por el que el campo resultante se anula.

En 0 <x < b

En la región intermedia entre los dos planos, la normal exterior del plano positivo es ahora $+{\vec {\imath }}$ mientras que la del plano negativo sigue siendo $-{\vec {\imath }}$. El campo neto es ahora

${\vec {E}}={\vec {E}}_{1}+{\vec {E}}_{2}={\frac {\sigma _{0}}{2\varepsilon _{0}}}(+{\vec {\imath }})+{\frac {(-\sigma _{0})}{2\varepsilon _{0}}}(-{\vec {\imath }})={\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}+{\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}={\frac {\sigma _{0}}{\varepsilon _{0}}}{\vec {\imath }}$

Los dos campos son ahora iguales en módulo, dirección y sentido, por lo que el campo neto es el doble de cada uno de ellos. Este campo es uniforme en toda la región entre los planos.

En x > b

En esta región, el vector normal exterior de ambos planos es $+{\vec {\imath }}$ por lo que el campo en esta región es también nulo

${\vec {E}}={\vec {E}}_{1}+{\vec {E}}_{2}={\frac {\sigma _{0}}{2\varepsilon _{0}}}(+{\vec {\imath }})+{\frac {(-\sigma _{0})}{2\varepsilon _{0}}}(+{\vec {\imath }})={\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}-{\frac {\sigma _{0}}{2\varepsilon _{0}}}{\vec {\imath }}={\vec {0}}$

Tenemos entonces que dos planos infinitos cargados uniformemente con cargas iguales y opuestas producen un campo uniforme entre los dos planos y nulo en el espacio exterior a los planos.

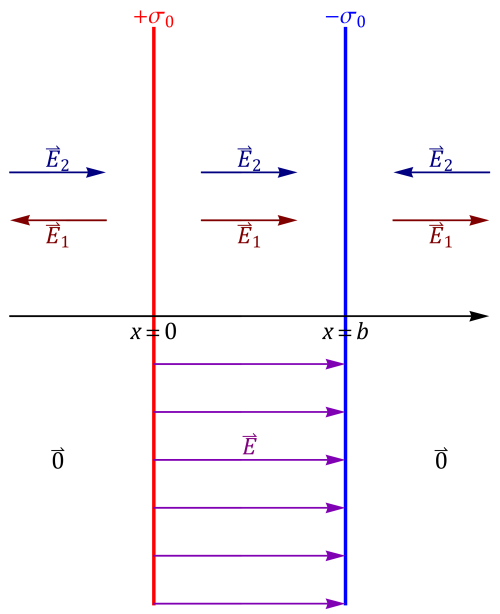
Nótese que no es que un plano impida que el campo del otro llegue al otro lado. Cada campo de cada plano se extiende hasta el infinito. Lo que ocurre es que el campo debido a las cargas de un plano anula el campo de las cargas del otro en el espacio exterior a los planos.