Diferencia entre revisiones de «Caso de coeficiente de dilatación»
Última edición de la página hace 9 meses por Antonio
(Página creada con «==Enunciado== En las proximidades de 20℃ la densidad de una sustancia sigue la gráfica lineal de la figura. ¿Cuánto vale el coeficiente de dilatación volumétrica a 20℃, en <math>(\,^\circ{}\mathrm{C})^{-1}</math>? <center>400px</center> ==Solución== El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como <center><math>\beta = -\frac{1}{\rho}\lefy(\frac{\partial \rho}{\partial T}\right)…») |
|||
| Línea 8: | Línea 8: | ||
El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como | El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como | ||
<center><math>\beta = -\frac{1}{\rho}\ | <center><math>\beta = -\frac{1}{\rho}\left(\frac{\partial \rho}{\partial T}\right)_p \simeq -\frac{1}{\rho}\,\frac{\Delta \rho}{\Delta T}</math></center> | ||
A 20℃ el valor de la densidad es | A 20℃ el valor de la densidad es | ||
Revisión del 08:53 19 feb 2025
Enunciado
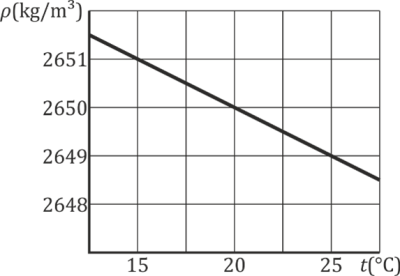
En las proximidades de 20℃ la densidad de una sustancia sigue la gráfica lineal de la figura. ¿Cuánto vale el coeficiente de dilatación volumétrica a 20℃, en ?
Solución
El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como
A 20℃ el valor de la densidad es
Para hallar la derivada calculamos la pendiente de la recta. Tomamos dos puntos de la cuadrícula y resulta
lo que nos da el coeficiente de dilatación




