Enunciado
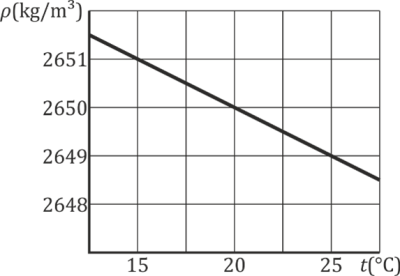
En las proximidades de 20℃ la densidad de una sustancia sigue la gráfica lineal de la figura. ¿Cuánto vale el coeficiente de dilatación volumétrica a 20℃, en  ?
?
Solución
El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \beta = -\frac{1}{\rho}\left(\frac{\partial \rho}{\partial T}\right)_p \simeq -\frac{1}{\rho}\,\frac{\Delta \rho}{\Delta T}}
A 20℃ el valor de la densidad es
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \rho(20\,^\circ{}\mathrm{C})=2650\,\frac{\mathrm{kg}}{\mathrm{m}^3}}
Para hallar la derivada calculamos la pendiente de la recta. Tomamos dos puntos de la cuadrícula y resulta
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\Delta\rho}{\Delta T}=\frac{2649-2650}{25-5}\,\frac{\mathrm{kg}}{\mathrm{m}^3{}^\circ{}\mathrm{C}}=-0.2\,\frac{\mathrm{kg}}{\mathrm{m}^3{}^\circ{}\mathrm{C}}}
lo que nos da el coeficiente de dilatación



