Calor y trabajo en un proceso lineal

Enunciado

Considere el caso del problema “Compresión lineal de un gas”, en el que se comprime cuasiestáticamente un gas ideal diatómico que inicialmente se encuentra a presión $p_{A}=100\,\mathrm {kPa}$, temperatura $T_{A}=300\,\mathrm {K}$ y ocupa un volumen $V_{A}=0.01\,\mathrm {m} ^{3}$, según la ley

$p=3p_{A}-{\frac {2p_{A}}{V_{A}}}V$

La compresión continúa hasta que la presión vale $p_{B}=2p_{A}$.

1. Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
2. Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.

Proceso completo

Trabajo

El proceso puede escribirse en forma numérica como

$p=300-20V\,$

con el volumen en L y la presión en kPa. El estado inicial cumple

$p_{A}=100\,\mathrm {kPa} \qquad V_{A}=10\,\mathrm {L} \qquad T_{A}=300\,\mathrm {K}$

y el final, tal como se ve en el problema citado

$p_{B}=200\,\mathrm {kPa} \qquad V_{B}=5\,\mathrm {L} \qquad T_{B}=300\,\mathrm {K}$

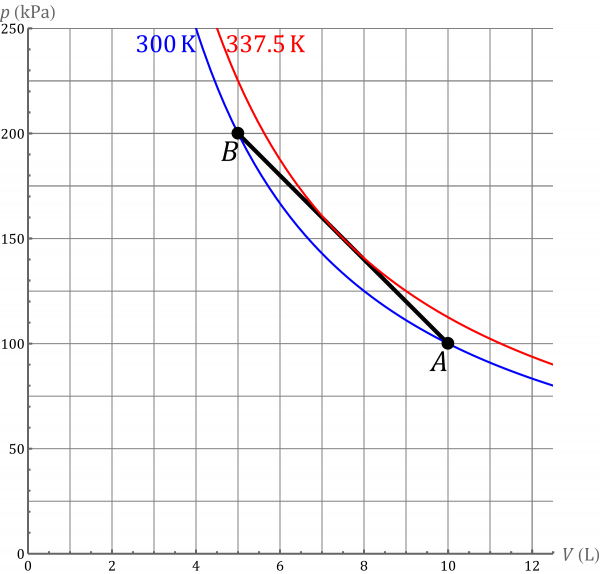
El proceso se describe mediante un segmento rectilíneo. El área bajo este segmento es el trabajo realizado, que será positivo por tratarse de una compresión. Podemos hallar este trabajo integrando

$W=-\int _{A}^{B}p\,\mathrm {d} V=-\int _{10}^{5}(300-20V)\mathrm {d} V=-\left.\left(300V-10V^{2}\right)\right|_{10}^{5}=750\,\mathrm {J}$

o directamente empleando el área de un trapecio

$W={\frac {p_{A}+p_{B}}{2}}(V_{A}-V_{B})={\frac {200+100}{2}}(10-5)\,\mathrm {J} =750\,\mathrm {J}$

Energía interna

La energía interna de un gas ideal depende solo de la temperatura. En este caso, la temperatura final en es la misma que la inicial, por lo que

$\Delta U=nc_{v}(T_{B}-T_{A})=0\,$

Calor

Obtenemos el calor intercambiado empleando el primer principio de la termodinámica

$Q=\Delta U-W=-750\,\mathrm {J}$

División en dos tramos

Tal como se ve en el problema citado, la temperatura aumenta hasta un máximo y luego vuelve a disminuir. El máximo se alcanza cuando $V_{C}=7.5\,\mathrm {L}$. Para este punto

$p_{C}=150\,\mathrm {kPa} \qquad \qquad T_{C}=337.5\,\mathrm {K}$

Dividimos entonces el proceso en dos.

Primer tramo

Entre A y C el trabajo corresponde de nuevo al área de un trapecio:

$W=(pA+pC)/2(VA-VC)={\frac {100+150}{2}}(10-7.5)\,\mathrm {J} =312.5\,\mathrm {J}$

La variación de energía ahora no es nula, pues la temperatura aumenta. Podemos hallar el cambio a partir de las presiones y volúmenes

$\Delta U=nc_{v}(T_{C}-T_{A})={\frac {p_{C}V_{C}-p_{A}V_{A}}{\gamma -1}}={\frac {150\cdot 7.5-100\cdot 10}{0.4}}=312.5\,\mathrm {J}$

lo que implica que en este tramo

$Q=\Delta U-W=312.5\,\mathrm {J} -312.5\,\mathrm {J} =0\,\mathrm {J}$

Vemos que aunque la temperatura se eleva, el cambio se debe a la entrada de trabajo, no de calor.

Segundo tramo

Calculamos el trabajo de la misma manera

$W=(pA+pC)/2(VA-VC)={\frac {150+200}{2}}(7.5-5.0)\,\mathrm {J} =437.5\,\mathrm {J}$

y la variación de la energía es ahora

$\Delta U=nc_{v}(T_{B}-T_{C})={\frac {p_{B}V_{B}-p_{C}V_{C}}{\gamma -1}}={\frac {200\cdot 5.0-150\cdot 7.5}{0.4}}=-312.5\,\mathrm {J}$

En este tramo se pierde toda la energía ganada en el tramo anterior.

El calor es ahora

$Q=\Delta U-W=-312.5\,\mathrm {J} -437.5\,\mathrm {J} =-750\,\mathrm {J}$

Todo el calor se expulsa en este segundo tramo.

Podíamos haber calculado estos valores simplemente restando los del primer tramo de los del proceso completo.