Diferencia entre revisiones de «Placa en escuadra rotatoria»
(Página creada con «==Enunciado== Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo <math>\theta(t)</math> que forma la barra <math>OX_0</math> con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vé…») |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
[[Archivo:placa-escuadra.png|right]] | |||
Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo <math>\theta(t)</math> que forma la barra <math>OX_0</math> con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vértices inferiores, A y B, una placa cuadrada de lado <math>L</math>, cuyo lado inferior AB mantiene en todo momento su horizontalidad respecto al plano “1”. | Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo <math>\theta(t)</math> que forma la barra <math>OX_0</math> con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vértices inferiores, A y B, una placa cuadrada de lado <math>L</math>, cuyo lado inferior AB mantiene en todo momento su horizontalidad respecto al plano “1”. | ||
# En función del ángulo <math>\theta</math>, localice geométricamente de forma razonada el centro instantáneo de rotación del movimiento {20}. Exprese su vector de posición relativo al punto O tanto en la base ligada al sólido “0” como en la ligada al sólido “1”. ¿Dónde se localiza el CIR del movimiento {21}? | # En función del ángulo <math>\theta</math>, localice geométricamente de forma razonada el centro instantáneo de rotación del movimiento {20}. Exprese su vector de posición relativo al punto O tanto en la base ligada al sólido “0” como en la ligada al sólido “1”. ¿Dónde se localiza el CIR del movimiento {21}? | ||
# En función de <math>\theta</math> y de <math>\dot{\theta}</math>, calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B. | # En función de <math>\theta</math> y de <math>\dot{\theta}</math>, calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B. | ||
==Centro instantáneo de rotación== | ==Centro instantáneo de rotación== | ||
Revisión del 19:14 13 ene 2024
Enunciado
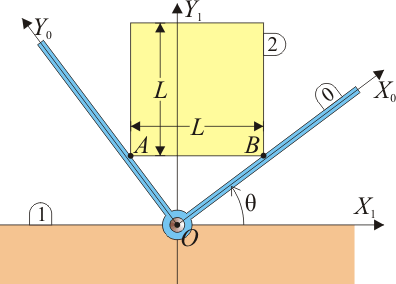
Se tiene un sistema formado por un plano horizontal (sólido “1”) en uno de cuyos puntos, O, se encuentra articulada una escuadra (sólido “0”) formada por dos barras ortogonales entre sí. Esta escuadra gira en torno a O, resultando variable el ángulo que forma la barra con el plano horizontal “1” (ver figura). Sobre la escuadra se encuentra permanentemente apoyada por sus vértices inferiores, A y B, una placa cuadrada de lado , cuyo lado inferior AB mantiene en todo momento su horizontalidad respecto al plano “1”.
- En función del ángulo , localice geométricamente de forma razonada el centro instantáneo de rotación del movimiento {20}. Exprese su vector de posición relativo al punto O tanto en la base ligada al sólido “0” como en la ligada al sólido “1”. ¿Dónde se localiza el CIR del movimiento {21}?
- En función de y de , calcule las velocidades de deslizamiento de la placa “2” respecto a la escuadra “0” en los puntos de contacto A y B.
Centro instantáneo de rotación
Posición del CIR {20}
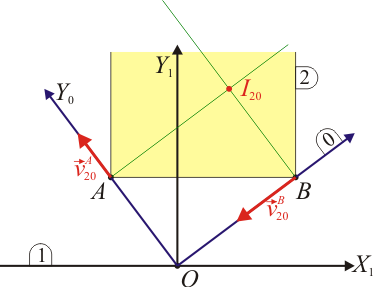
Localizamos la posición del CIR a partir de la velocidad de dos puntos en dicho movimiento. En este caso, lo más sencillo es considerar los dos puntos de contacto A y B.
En estos dos puntos se cumple que la placa no puede atravesar a la escuadra y por tanto la velocidad de los puntos A y B debe ser tangencial a las barras de la escuadra, esto es, respectivamente a lo largo de los ejes y
Estas velocidades deben ser ortogonales a los vectores de posición relativos al centro instantáneo de rotación . Por ello, trazamos las perpendiculares a las barras de la escuadra en los puntos A y B. Su intersección es el CIR .
Este punto se encuentra en el vértice de un rectángulo cuyo vértice opuesto es el punto O y una de cuyas diagonales es el lado AB de la placa.
Expresión en la base “0”
La posición del CIR en la base “0” es inmediata observando que se encuentra en el vértice de un rectángulo cuyo vértice opuesto es O. Por adición de vectores se cumple
y por tratarse de un paralelogramo
así que la posición del CIR respecto a O es
Los dos sumandos se encuentran en la dirección de los ejes

Las dos distancias las obtenemos observando que el triángulo OBA es rectángulo en O, su hipotenusa mide y el ángulo en el vértice B es igual a . Por ello
y la posición del CIR expresada en la base ligada al sólido “0” vale
Este resultado nos dice que en el sistema “0”, las sucesivas posiciones del CIR forman un arco de circunferencia de radio y tal que el vector de posición del CIR forma un ángulo con el eje
Expresión en la base “1”
Una vez que tenemos la expresión en el sistema “0” es inmediato pasarla al sistema “1” simplemente relacionando las bases vectoriales. Se cumple
Sustituyendo en la expresión obtenida en la sección anterior
Agrupando términos
En esta expresión reconocemos las razones trigonométricas del ángulo doble:
También podemos llegar a este resultado geométricamente, observando que si el ángulo que forma el vector con el eje vale y el que éste forma con el vale también , el que forma con es igual a , de donde es inmediato el vector de posición anterior.
Localización del CIR {21}

El movimiento {21} es una traslación, ya que la orientación de la placa “2” no cambia respecto al sólido “1” aunque se desplace. Por ello, el CIR se encontrará en el infinito.
Por el teorema de los tres centros, los CCIIR , e se encuentran alineados. es el punto O de articulación de la escuadra con el plano horizontal. El es el que hallamos en la sección anterior. Por tanto, el CIR se encuentra en el infinito según la recta que pasa por estos dos puntos, que es una que forma un ángulo con el eje .
Velocidades de deslizamiento
Podemos hallar las dos velocidades de deslizamiento con ayuda del CIR o derivando los vectores de posición.
Por derivación
Conocemos la posición de ambos puntos en el sistema “0” en todo momento
Derivando en ambas expresiones obtenemos, para el punto A
y para el punto B
Con ayuda del CIR
Se trata de hallar las velocidades de A y B en el movimiento relativo de la placa “2” respecto a la escuadra “0”. En cada instante se verifica
siendo los vectores de posición relativos
La velocidad angular la da la derivada temporal del ángulo que forman la placa y la escuadra. Su sentido lo da la regla de la mano derecha. Cuando el ángulo aumenta la placa gira en sentido horario respecto a la escuadra, por lo que
Alternativamente podemos obtener esta rotación observando que {21} es una traslación y que {01} tiene velocidad angular
Sustituyendo en la expresión del campo de velocidades hallamos las velocidades de deslizamiento. Para el punto A
y para el B




































