Segunda Convocatoria Ordinaria 2021/22 (G.I.C.)

Barra rotando alrededor de su centro con muelle, en equilibrio estático

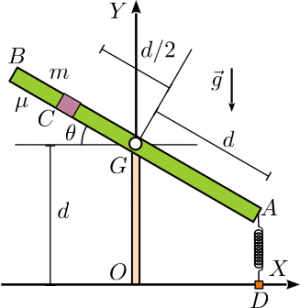
Una barra delgada, de masa despreciable y longitud $2d$, esta articulada y puede rotar alrededor de su punto central $G$. El extremo $A$ está conectado a un muelle de constante elástica $k=mg/d$ y longitud natural nula. El otro extremo del muelle se conecta en $D$ a un pasador, de modo que el muelle siempre se mantiene vertical. En el punto $C$ de la placa se encuentra una argolla de masa $m$ que puede deslizar sobre la barra (esta argolla se trata como una masa puntual) El contacto entre la argolla y la barra es rugoso, con coeficiente de rozamiento estático $\mu$. La gravedad actúa como se indica en la figura.

1. Escribe los vectores ${\overrightarrow {OD}}$ y ${\overrightarrow {OA}}$ en la base vectorial asociada a los ejes de la figura.
2. Dibuja los diagramas de fuerza de la barra y de la masa.
3. Encuentra para que valor o valores de $\theta$ hay equilibrio mecánico y los valores de todas las fuerzas en esa situación.
4. En la situación del apartado anterior, ¿qué condición debe cumplir $\mu$ para que la masa no deslice?

Barra rotando alrededor de su centro con muelle

Tenemos una configuración similar a la del problema anterior, pero sin muelle. Además, ahora la barra tiene una masa de valor también $m$. Además, supondremos que el rozamiento es tan grande que la argolla no desliza en ningún momento a lo largo de la barra. La figura muestra el instante inicial en el que la barra y la masa está en reposo. \begin{enumerate}

 \item Encuentra la expresión que da la energía potencial del sistema en la posición inicial.
 \item Calcula la velocidad de rotación de la barra y la velocidad de la argolla cuando el extremo $B$ 
   de la barra coincide con el punto $O$.

\end{enumerate} \textbf{Nota:} El momento de inercia de una barra de masa de masa $m$ y longitud $L$ respecto a un eje perpendicular a ella que pasa por su centro es $mL^2/12$.