Rodadura permanente de un disco

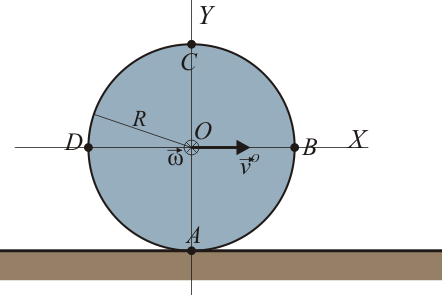
Enunciado

La rodadura permanente de un disco de radio $R$ sobre una superficie horizontal puede describirse mediante el campo de velocidades

${\vec {v}}^{P}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OP}}\,\,;\qquad {\vec {v}}^{O}=v_{0}{\vec {\imath }}\,\,;\qquad {\vec {\omega }}=-{\frac {v_{0}}{R}}{\vec {k}}$

donde la superficie horizontal se encuentra en $y=-R$.

1. Determine, para un instante dado, la velocidades de los puntos A, B, C y D situados en los cuatro cuadrantes del disco.
2. Suponiendo $v_{0}=\mathrm {cte} \,$, calcule la aceleración de dichos puntos para el mismo instante.

Velocidades

Para cada uno de los puntos, basta aplicar la fórmula correspondiente

Punto A

Su vector de posición relativa es

${\overrightarrow {OA}}=-R{\vec {\jmath }}$

por lo que su velocidad vale

${\vec {v}}^{A}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OA}}=v_{0}{\vec {\imath }}+\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&0&-v_{0}/R\\0&-R&0\end{matrix}}\right|={\vec {0}}$

Punto B

${\overrightarrow {OB}}=R{\vec {\imath }}$    ${\vec {v}}^{B}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OB}}=v_{0}{\vec {\imath }}+\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&0&-v_{0}/R\\R&0&0\end{matrix}}\right|=v_{0}({\vec {\imath }}-{\vec {\jmath }})$

Punto C

${\overrightarrow {OC}}=R{\vec {\jmath }}$    ${\vec {v}}^{C}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OC}}=v_{0}{\vec {\imath }}+\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&0&-v_{0}/R\\0&R&0\end{matrix}}\right|=2v_{0}{\vec {\imath }}$

Punto D

${\overrightarrow {OB}}=-R{\vec {\imath }}$    ${\vec {v}}^{D}={\vec {v}}^{O}+{\vec {\omega }}\times {\overrightarrow {OD}}=v_{0}{\vec {\imath }}+\left|{\begin{matrix}{\vec {\imath }}&{\vec {\jmath }}&{\vec {k}}\\0&0&-v_{0}/R\\-R&0&0\end{matrix}}\right|=v_{0}({\vec {\imath }}+{\vec {\jmath }})$

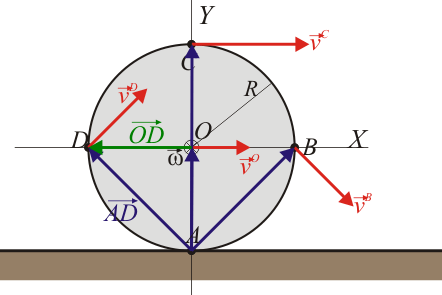
Obtenemos que el punto de contacto con el suelo posee velocidad instantánea nula, mientras que el punto superior posee velocidad doble a la de avance de la rueda.

Las velocidades de los puntos O, B, C y D son perpendiculares al vector de posición relativo al punto A, como corresponde a que este se encuentre en el eje instantáneo de rotación:

${\vec {v}}^{P}=\overbrace {{\vec {v}}^{A}} ^{={\vec {0}}}+{\vec {\omega }}\times {\overrightarrow {AP}}={\vec {\omega }}\times {\overrightarrow {AP}}\perp {\overrightarrow {AP}}$

Aceleraciones

La expresión general del campo de aceleraciones es

${\vec {a}}^{P}={\vec {a}}^{O}+{\vec {\alpha }}\times {\overrightarrow {OP}}+{\vec {\omega }}\times ({\vec {\omega }}\times {\overrightarrow {OP}})$

En este caso tenemos que la velocidad del punto O es constante, por lo que

${\vec {a}}^{O}={\frac {\mathrm {d} {\vec {v}}^{O}}{\mathrm {d} t}}={\frac {\mathrm {d} v_{0}}{\mathrm {d} t}}{\vec {\imath }}={\vec {0}}$

También es nula la aceleración angular

${\vec {\alpha }}={\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}={\vec {0}}$

lo que nos deja con

${\vec {a}}^{P}={\vec {\omega }}\times ({\vec {\omega }}\times {\overrightarrow {OP}})$

Desarrollando el doble producto vectorial

${\vec {a}}^{P}=({\vec {\omega }}\cdot {\overrightarrow {OP}}){\vec {\omega }}-\omega ^{2}{\overrightarrow {OP}}$

Para los cuatro puntos del enunciado, el vector de posición relativo al punto O está contenido en el plano OXY y es por tanto perpendicular a la velocidad angular, con lo que la aceleración de cada uno se reduce a

${\vec {a}}^{P}=-\omega ^{2}{\overrightarrow {OP}}=-{\frac {v_{0}^{2}}{R^{2}}}{\overrightarrow {OP}}$

En los cuatro casos resulta radial y hacia adentro del disco, lo que nos da las cuatro aceleraciones

${\vec {a}}^{A}={\frac {v_{0}^{2}}{R}}{\vec {\jmath }}$    ${\vec {a}}^{B}=-{\frac {v_{0}^{2}}{R}}{\vec {\imath }}$    ${\vec {a}}^{C}=-{\frac {v_{0}^{2}}{R}}{\vec {\jmath }}$    ${\vec {a}}^{D}={\frac {v_{0}^{2}}{R}}{\vec {\imath }}$