Disco desenrollándose de una cuerda (G.I.A.)

Enunciado

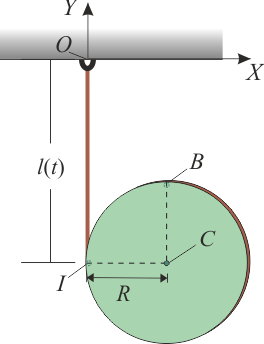
Un disco de radio $R$ gira y cae, siempre contenido en el plano vertical $OXY$, mientras se desenrolla de una cuerda que pende verticalmente, y cuya longitud aumenta según la ley horaria $l(t)=R+K\!\ t^{2}$ (donde $K$ es una constante conocida).

1. Obtenga la reducción cinemática que describe el movimiento instantáneo del disco.
2. Velocidad y aceleración instantáneas del punto $B$ indicado en la figura.

Solución

Descripción del movimiento instantáneo

Reducción cinemática

Como sabemos, el movimiento del disco respecto del sistema de referencia fijo queda caracterizado en cada instante por los dos vectores que forman la reducción cinemática: el vector rotación instantánea ${\vec {\omega }}$ y la velocidad de un punto cualquiera de dicho sólido. En el sistema bajo estudio, en que el disco se mueve siempre contenido en el plano $OXY$, hay un punto cuya velocidad instantánea es fácil de determinar: se trata del centro del disco $C$, que se moverá siempre paralelo a la cuerda desenrollada (y, por tanto, al eje $OY$), y según la ley horaria $l(t)$. Es decir, proponemos la reducción cinemática

$S=\{{\vec {\omega }}(t);\ {\vec {v}}_{C}(t)\}\,\mathrm {,} \,\quad \,\mathrm {tal} \;\,\mathrm {que} \quad {\vec {v}}_{P}(t)={\vec {v}}_{C}(t)+{\vec {\omega }}(t)\times {\overrightarrow {CP}}\,\mathrm {,} \;\;\,\forall P\in \tau _{\mathrm {disco} }$

Comencemos determinado la expresión instantánea de la velocidad del centro del disco. En todo instante, el radio-vector ${\vec {r}}_{C}$ que determina la posición del centro $C$ respecto del punto fijo $O$, adoptado como origen del sistema de referencia, puede expresarse como sigue:

${\vec {r}}_{C}={\overrightarrow {OC}}={\overrightarrow {OI}}+{\overrightarrow {IC}}\quad \Longrightarrow \quad {\vec {r}}_{C}(t)=-l(t)\!\ {\vec {\jmath }}+R{\vec {\imath }}=R{\vec {\imath }}-{\big (}R+K\!\ t^{2}{\big )}\!\ {\vec {\jmath }}$

siendo $I$ el punto geométrico donde la cuerda desenrrollada se separa del disco. La derivada temporal de las ecuaciones horarias que describen el movimiento del centro del disco, nos proporciona la expresión que indica cómo es, en el transcurso del tiempo, la velocidad instantánea de dicho punto:

${\vec {v}}_{C}(t)={\frac {\mathrm {d} {\vec {r}}_{C}}{\mathrm {d} t}}=-2Kt\!\ {\vec {\jmath }}$

Para obtener el vector rotación instantánea, comenzaremos por determinar su dirección. Para ello utilizaremos la informació de que el disco se mueve siempre contendio en el plano $OXY$. En consecuencia, los desplazamientos instantáneos de todos los punos del disco, en cualquier instante, punto del disco deben estar contenidos en dicho plano, olo que es lo mismo, deben ser perpendiculares al unitario ${\vec {k}}$ que indica la dirección del eje $OZ$:

$\forall P\in \tau _{\mathrm {disco} },\quad \,{\vec {k}}\perp \mathrm {d} {\vec {r}}_{P}={\vec {v}}_{P}\!\ \mathrm {d} t$

Como se demostró en el primer ejercicio, el vector rotación puede determinarse a partir de velocidades de tres puntos no alineados: por ejemplo, los puntos $C$, $I$ y $B$. Sabemos de éstas que son vectores siempre contenidos en el plano $OXY$, al igual, por tanto, que cualquier vector obtenidos como una combinacional lineal de áquellos. Así, se tendrá:

$\left.{\begin{array}{c}\displaystyle ({\vec {v}}_{B}-{\vec {v}}_{C})\perp {\vec {k}}\\\\\displaystyle ({\vec {v}}_{I}-{\vec {v}}_{C})\perp {\vec {k}}\end{array}}\right\}\quad \Longrightarrow \quad {\vec {\omega }}(t)={\frac {({\vec {v}}_{B}-{\vec {v}}_{C})\times ({\vec {v}}_{I}-{\vec {v}}_{C})}{{\overrightarrow {BC}}\cdot ({\vec {v}}_{I}-{\vec {v}}_{C})}}\!\ \|\!\ {\vec {k}}\qquad \to \qquad$${\vec {\omega }}(t)=\omega (t)\!\ {\vec {k}}$

Y una vez determinada la dirección del vector rotación, basta con conocer la velocidad de otro punto del disco en el instante genérico $t$, para obtener la ley $\omega (t)$. Para ello, consideremos el punto geométrico $I(t)$ que, en cada instante, coincide con el extremo inferior del tramo de cuerda desenrollada. Respecto del sistema de referencia fijo, este punto se va desplazando según la ley horaria $l(t)$:

${\overrightarrow {OI}}(t)=-l(t)\!\ {\vec {\jmath }}=-(R+K\!\ t^{2})\!\ {\vec {\jmath }}$

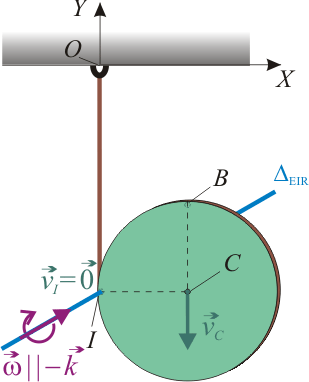
La derivada temporal de estas ecuaciones horarias es la velocidad con la que se desplaza el punto geométrico $I$, pero ésta no es la velocidad del punto $I$ del disco que, en el instante arbitrario considerado, coincide con la posición de dicho punto geométrico $I(t)$. Obsérvese que, los puntos del perímetro del disco se mueven solidariamente con los de la cuerda enrollada. En particular, el punto del disco que en el instante $t$ se encuentra en la posición coincidente con $I(t)$, tendrá la misma velocidad ${\vec {v}}_{I}$ que el punto de la cuerda que en dicho instante coincide tambien con el punto geométrico $I(t)$. Nótese que, una vez desenrrollada la cuerda, los puntos de ésta permanecerán en un posición fija (reposo permanente); por tanto, el punto de la cuerda que coincide con $I(t)$ tendrá velocidad nula desde el instante $t$. En consecuencia, el punto del disco que en dicho instante arbitrario $t$ coincide con el punto geométrico $I(t)$, también tendrá velocidad nula, aunque sólo estará en resposo de forma instantánea. Es decir, sea $I$ el punto del perímetro del disco que en el instante $t$ coincide con el extremo inferior de la cuerda desenrollada; se tendrá que...

${\vec {v}}_{I}(t)={\vec {0}}\,\mathrm {,} \quad \,\mathrm {con} \;\;{\overrightarrow {CI}}=-R\!\ {\vec {\imath }}$

Si aplicamos el teorema de Chasles en el instante genérico $t$...

${\vec {v}}_{I}(t)={\vec {0}}={\vec {v}}_{C}(t)+{\vec {\omega }}(t)\times {\overrightarrow {CI}}=-2Kt\!\ {\vec {\jmath }}-R\omega (t)\!\ {\bigg (}{\vec {k}}\times {\vec {\imath }}\!\ {\bigg )}\qquad \to \qquad$$\omega (t)=-{\frac {2Kt}{R}}$

En resumen, la reducción cinematica en el centro $C$ del disco, en un instante de tiempo arbitrario $t$ es...

$S=\left\{{\begin{array}{l}\displaystyle {\vec {\omega }}(t)=\omega (t)\!\ {\vec {k}}=-{\frac {2Kt}{R}}\!\ {\vec {k}}\\\\\displaystyle {\vec {v}}_{C}(t)=v(t)\!\ {\vec {\jmath }}=-2Kt\!\ {\vec {\jmath }}\end{array}}\right.$

Tipo de movimiento

La reducción cinemática obtenida nos indica que el disco se mueve en todo instante y que su movimiento no es una traslación ya que, tanto la velocidad del punto $C$, como el vector rotación instantánea son siempre no nulos. Sin embargo, si comprobamos el valor del invariante escalar...

${\vec {\omega }}(t)\perp {\vec {v}}_{C}(t)\quad \Longrightarrow \quad {\vec {\omega }}(t)\cdot {\vec {v}}_{C}(t)=0={\vec {\omega }}(t)\cdot {\vec {v}}_{P}(t)\,\mathrm {,} \,\;\;\forall P\in \tau _{\mathrm {disco} }\;\;\,\mathrm {y} \,\;\;\forall \,t$

Por tanto, el movimiento del disco es, en todo instante, una rotación. El eje de rotación $\Delta _{\mathrm {EIR} }$ es, por definición, siempre paralelo al vector rotación instantánea y, como éste, tendrá dirección constante: la del unitario ${\vec {k}}$, siempre perpendicular al plano que contine al disco. Por otra parte, como la velocidad mínima es nula,

$v_{m}(t)={\frac {{\vec {\omega }}(t)\cdot {\vec {v}}_{C}(t)}{|{\vec {\omega }}(t)|}}=0\,\mathrm {,} \,\;\;\forall \ t$

aquellos puntos del disco que se encuentren en reposo pertenecerán a dicho eje. Como vimos anteriormente, esto ocurre de forma instantánea con el punto del disco que en cada instante coincide con el punto geométrico $I(t)$ donde la cuerda desenrollada se separa del disco, por tanto...

${\vec {v}}_{I}(t)={\vec {0}}\quad \Longrightarrow \quad I(t)\in \Delta _{\mathrm {EIR} }\!\ \|\!\ {\vec {k}}$

Y como en el transcurso del movimiento, este punto cambia su posición respecto del sistema de referencia fijo, también lo hará el eje de rotación $\Delta _{\mathrm {EIR} }$que será, por tanto, de caractér instantáneo:

$\Delta _{\mathrm {EIR} }(t):\ {\overrightarrow {OX}}(t)={\overrightarrow {OI}}(t)+\lambda \!\ {\vec {k}}=-(R+K\!\ t^{2}){\vec {\jmath }}+\lambda \!\ {\vec {k}}\,\mathrm {,} \,$  $\lambda \in \mathrm {I} \!\mathrm {R}$

Por otra parte, obsérvese que la reducción cinemática en el centro del disco, $C$, no es la reducción canónica. Ésta tiene como centro de reducción un punto del eje de rotación; en el sistema analizado se tendrá:

$S^{\mathrm {can} }=\left\{{\begin{array}{l}\displaystyle {\vec {\omega }}(t)=\omega (t)\!\ {\vec {k}}=-{\frac {2Kt}{R}}\!\ {\vec {k}}\\\\\displaystyle {\vec {v}}_{I}(t)={\vec {0}}\,\mathrm {;} \,\quad \,\mathrm {con} \,\;\;{\overrightarrow {CI}}=-R\!\ {\vec {\imath }}\end{array}}\right.$

Obsérvese que el disco rueda sin deslizar sobre la cuerda cuando ésta se se desenrolla del disco.

Propiedades cinemáticas del punto $B$

Velocidad instantánea

Para determinar la velocidad instantánea del punto $B$, aplicamos el teorema de Chasles con cualquiera de las dos reducciones cinemáticas propuestas en el apartado anterior. Si utilizamos la reducción en el centro del disco...

$\left.{\begin{array}{l}\displaystyle {\vec {v}}_{B}(t)={\vec {v}}_{C}(t)+{\vec {\omega }}(t)\times {\overrightarrow {CB}}\\\\\displaystyle {\overrightarrow {CB}}=R\!\ {\vec {\jmath }}\end{array}}\right\}\;\Longrightarrow \quad {\vec {v}}_{B}(t)=v(t)\!\ {\vec {\jmath }}\!\ +\!\ R\!\ \omega (t)\!\ {\big (}{\vec {k}}\times {\vec {\jmath }}\!\ {\big )}$   ⇒   ${\vec {v}}_{B}(t)=2Kt\!\ {\big (}{\vec {\imath }}-{\vec {\jmath }}\!\ {\big )}$

Y empleando la reducción canónica...

$\left.{\begin{array}{l}\displaystyle {\vec {v}}_{B}(t)=\overbrace {{\vec {v}}_{I}(t)} ^{={\vec {0}}}+{\vec {\omega }}(t)\times {\overrightarrow {IB}}\\\\\displaystyle {\overrightarrow {IB}}={\overrightarrow {IC}}+{\overrightarrow {CI}}=R\!\ {\vec {\imath }}\!\ +\!\ R\!\ {\vec {\jmath }}\end{array}}\right\}\;\Longrightarrow \quad {\vec {v}}_{B}(t)=\!\ R\!\ \omega (t)\!\ {\big [}{\vec {k}}\times ({\vec {\imath }}+{\vec {\jmath }}\!\ ){\big ]}$   ⇒   ${\vec {v}}_{B}(t)=2Kt\!\ {\big (}{\vec {\imath }}-{\vec {\jmath }}\!\ {\big )}$

Aceleración instantánea

En este caso aplicaremos la expresión del campo de aceleraciones del sólido rígido. Para ello, debemos conocer el valor de las derivadas de los elementos de la reducción en el instante considerado. Si optásemos por utilizar la reducción canónica, nos encontraríamos con que podemos determinar la aceleración angular o derivada temporal del vector rotación instantánea, pues tenemos la expresión que describe cómo este vector depende del tiempo. Pero no conocemos el valor de la aceleración instantánea del punto del disco que en el instante $t$ ocupa la posición geométrica $I(t)$. Lo único que sabemos es que, en dicho instante, su velocidad es nula pero su aceleración debe ser necesariamente distinta de cero, pues dicho punto del disco sólo se encuentra en un estado de reposo instantáneo, ya que en $t+\mathrm {d} t$ ocupará una nueva posición.

Sin embargo, la reducción cinemática con centro de reducción en $C$ nos permite, además, determinar la aceleración instantánea de dicho punto, pues conocemos la dependencia temporal de la velocidad de dicho punto:

${\frac {\mathrm {d} }{\mathrm {d} t}}[S]=\left\{{\vec {\alpha }}(t);\!\ {\vec {a}}_{C}(t)\right\}\,\mathrm {,} \,\;\;\,\mathrm {siendo} \,\;\;\left\{{\begin{array}{l}\displaystyle {\vec {\alpha }}(t)={\frac {\mathrm {d} {\vec {\omega }}}{\mathrm {d} t}}=-{\frac {2K}{R}}\ {\vec {k}}\\\\\displaystyle {\vec {a}}_{C}(t)={\frac {\mathrm {d} {\vec {v}}_{C}}{\mathrm {d} t}}=-2K\!\ {\vec {\jmath }}\end{array}}\right.$

Para obtener la aceleración del punto del disco que en el instante arbitrario $t$ ocupa la posición $B$ aplicamos...

${\vec {a}}_{B}(t)={\vec {a}}_{C}(t)+{\vec {\alpha }}(t)\times {\overrightarrow {CB}}+{\vec {\omega }}(t)\times {\big [}{\vec {\omega }}(t)\times {\overrightarrow {CB}}{\big ]}$   ⇒   ${\vec {a}}_{B}(t)=2K\!\ {\vec {\imath }}\!\ -\!\ 2K\left(1+{\frac {2Kt^{2}}{R}}\right){\vec {\jmath }}$