Problemas de dinámica de la partícula (GIOI)

Masa que cuelga de dos hilos

En la situación de equilibrio de una masa atada con dos hilos, ilustrada en la figura, ¿cuánto valen los módulos de las tensiones respectivas?

Solución

Masa que cuelga de dos hilos oblicuos

Un peso de 16.8N cuelga del techo suspendido de dos hilos situados como indica la figura. Calcule la tensión de cada hilo.

Solución

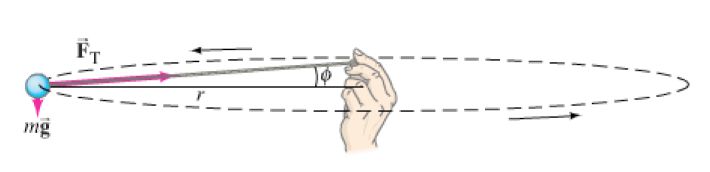
Masa girando alrededor de una mano

Una masa de 0.5 kg situada en el extremo de una cuerda de 50 cm de longitud se hace girar horizontalmente con la mano de manera que da 2 vueltas por segundo. ¿Puede estar la cuerda completamente horizontal? Determine la tensión de la cuerda y el ángulo que forma con la horizontal.

Solución

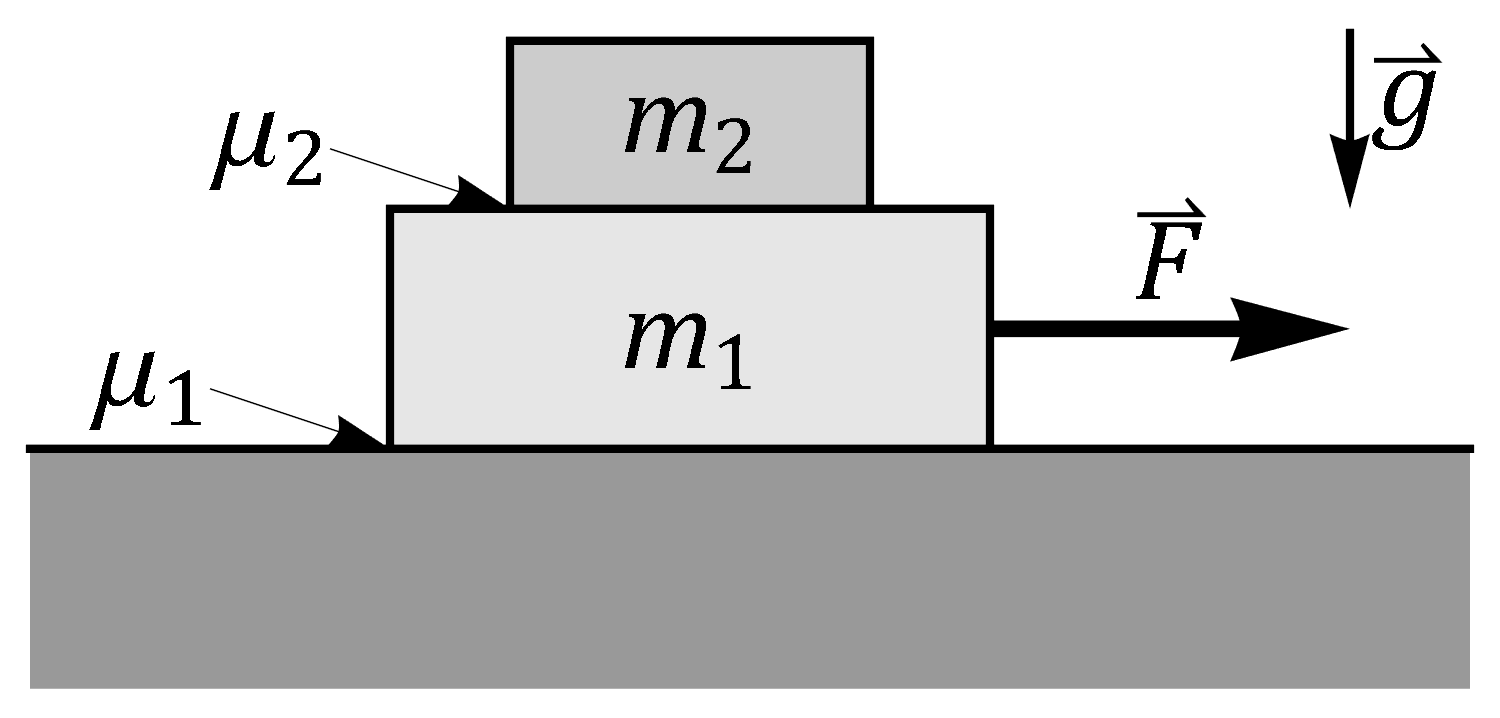
Dos bloques apilados

Sobre una mesa horizontal se encuentran apilados dos bloques, siendo el inferior de masa $m_{1}$ y el superior de masa $m_{2}$. El coeficiente de rozamiento estático del bloque inferior con la mesa vale $\mu _{1}$ y el del segundo bloque con el primero $\mu _{2}$. Los coeficientes de rozamiento dinámico valen lo mismo que los estáticos.

1. Para el estado de reposo y sin fuerzas laterales aplicadas, indique la fuerza que la mesa ejerce sobre el bloque inferior y el que éste ejerce sobre el superior.
2. Suponiendo $\mu _{1}=0$, se tira del bloque inferior con una fuerza horizontal $F$. ¿Qué fuerzas actúan sobre cada bloque? ¿Cuánto debe valer como mínimo esta fuerza si se quiere que el bloque superior se quede atrás? ¿Cuánto vale la aceleración de cada bloque para valores de la fuerza inferiores o superiores a este valor crítico?
3. Resuelva las mismas cuestiones que en el apartado anterior, suponiendo ahora $\mu _{1}\neq 0$.
4. Calcule los valores de las diferentes fuerzas y las aceleraciones si $m_{1}=3.00\,\mathrm {kg}$, $m_{2}=2.00\,\mathrm {kg}$, $\mu _{1}=0.30$, $\mu _{2}=0.50$ para (a) $F=10.0\,\mathrm {N}$ (b) $F=20.0\,\mathrm {N}$ (c) $F=50.0\,\mathrm {N}$

Solución

Doble máquina de Atwood

Se tiene el sistema de dos poleas y tres masas de la figura 5 ($m_{1}=4\,\mathrm {kg}$, $m_{2}=1\,\mathrm {kg}$, $m_{3}=3\,\mathrm {kg}$). Los dos hilos son ideales (inextensibles y sin masa) y las poleas son ideales (sin masa ni fricción). Para este sistema calcule

1. La aceleración de cada una de las masas.
2. La tensión de cada uno de los dos cables.
3. La fuerza que hace el soporte que sujeta el sistema al techo.

Suponga ahora que se sujeta la masa $m_{3}=3\,\mathrm {kg}$, de manera que no puede moverse.

4. ¿Cuál es en ese caso la aceleración de cada una de las otras dos masas?
5. ¿Cuánto vale la tensión de cada cable?
6. ¿Qué fuerza hace el soporte superior y cuál el individuo que sujeta la masa $m_{3}$?

Tome g=9.8\,m\/s^2.