Aro articulado en el extremo de una barra (Jun. 2023)

Enunciado

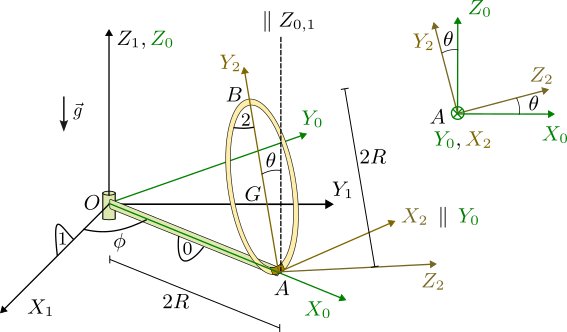
Una barra (sólido "0") homogénea y delgada de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2R} y masa despreciable está articulada en el punto fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O} . La barra está siempre contenida en el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_1Y_1} y rota alrededor del eje fijo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OZ_1} . El sistema de ejes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0Y_0Z_0} se elige de modo que el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OX_0} contenga siempre a la barra. Un aro (sólido "2") de radio Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle R} y masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} , se articula sobre el extremo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} de la barra "0", de modo que puede rotar alrededor del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_2} , paralelo en todo momento al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OY_0} . El sistema de ejes "2" se elige de modo que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Z_2} sea perpendicular al plano del aro y el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_2} sea paralelo al Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_0} . De este modo, el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_2} contiene siempre al centro del aro y el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Y_2Z_2} coincide con el plano Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle X_0Z_0} El aro no rota alrededor del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Z_2} . El sistema está sometido a la acción de la gravedad, como se indica en la figura.

Nota: Utiliza la base vectorial asociada al sólido "0" para hacer todos los cálculos.

• Expresa los vectores de la base del sistema "2" en función de los vectores de la base "0", y los de la base "0" en función de los de la base "2".
• Encuentra la reducción cinemática de los movimientos {01}, {20} y {21} en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} .
• Calcula la cantidad de movimiento del aro y el o angular del aro en su centro de masas.
• Dibuja el diagrama de fuerzas y momentos sobre la barra y el aro.
• Escribe la expresión genérica de las fuerzas y momentos activos y vinculares que actúan sobre cada sólido. ¿Cuántas incógnitas tiene el problema?
• Escribe la expresión vectorial del T.C.M. y el T.M.C. aplicados a los dos sólidos ¿Cuántas ecuaciones pueden obtenerse? (No hay que escribir las ecuaciones)
• Escribe la energía potencial total del sistema "0" + "2".
• ¿Qué integral o integrales primeras del sistema "0" + "2" existen? ¿Por qué? (No hay que escribir las expresiones).

Supondremos a partir de ahora que la función de Lagrange tiene la forma Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle {\cal L} = A\dot{\phi}^2\sen\phi + B\dot{\theta}^2 + C\cos\theta, } siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C} constantes conocidas.

• Aplica el método de los multiplicadores de Lagrange para encontrar las ecuaciones que describen el movimiento de los sólidos si se verifican estas dos ligaduras:

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle g_1 = \dot{\theta} - \omega_0 = 0, \qquad g_2 = 2\dot{\phi} - \omega_0 = 0. }

• En Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle t=0^-} tenemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \phi(0)=\pi/4} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta(0)=0} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}(0^-)=\dot{\theta}(0^-)=0} . Se aplica una percusión Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\hat{F}}=\hat{F}_0\,(\vec{\imath}_0 + \vec{\jmath}_0)} en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B} del aro. Determina el valor de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\phi}(0^+)} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}(0^+)} . (Las ligaduras del apartado anterior no se aplican en este apartado)

Solución

Bases de los sólidos "2" y "0"

Los vectores de la base "2" son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{\imath}_2 = \vec{\jmath}_0,\\ \vec{\jmath}_2 = -\mathrm{sen}\,\theta\,\vec{\imath}_0 + \cos\theta\,\vec{k}_0,\\ \vec{k}_2 = \cos{\theta}\,\vec{\imath}_0 + \mathrm{sen}\,\theta\,\vec{k}_0. \end{array} }

Los vectores de la base "0" son

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{\imath}_0 = -\mathrm{sen}\,\theta\,\vec{\jmath}_2 + \cos\theta\,\vec{k}_2,\\ \vec{\jmath}_0 = \vec{\imath}_2,\\ \vec{k}_0 = \cos{\theta}\,\vec{\jmath}_2 + \mathrm{sen}\,\theta\,\vec{k}_2. \end{array} }

Reducciones cinemáticas

Para el movimiento {01} tenemos que el eje del movimiento coincide con el eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle OZ_{01}} . Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{01} = \dot{\phi}\,\vec{k}_0, \qquad \vec{v}^{\,O}_{01} = \vec{0}. }

Luego nos hará falta la velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,A}_{01}} . Aplicamos la ecuación del campo de velocidades de este movimiento

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{ll} \vec{v}^{\,A}_{01} & = \vec{v}^{\,O}_{01} + \vec{\omega}_{01}\times\overrightarrow{OA}\\ & \vec{v}^{\,O}_{01} = \vec{0}. \\ & \vec{\omega}_{01}\times\overrightarrow{OA} = 2R\dot{\phi}\,\vec{\jmath}_0.\\ & \qquad\overrightarrow{OA} = 2R\,\vec{\imath}_0. \end{array} }

Para el movimiento {20} vemos que el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A} del aro y la barra son siempre el mismo. Además, a partir del dibujo con los ejes "2" y "0", tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{\omega}_{20} = -\dot{\theta}\,\vec{\jmath}_0, \qquad \vec{v}^{\,A}_{20} = \vec{0}. }

Para el movimiento {21} usamos las leyes de composición para la combinación {21} = {20} + {01}. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} = -\dot{\theta}\,\vec{\jmath}_0 + \dot{\phi}\,\vec{k}_0. \end{array} }

Cantidad de movimiento y momento angular del aro

La cantidad de movimiento del aro es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{C}_2 = m\vec{v}^{\,G}_{21}. }

Utilizamos la reducción cinemática del movimiento {21} en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{ll} \vec{v}^{\,G}_{21} & = \vec{v}^{\,A}_{21} + \vec{\omega}_{21}\times\overrightarrow{AG} = -R\dot{\theta}\cos\theta\,\vec{\imath}_0 - R\dot{\phi}(2-\mathrm{sen}\theta)\,\vec{\jmath}_0 - R\dot{\theta}\mathrm{sen}\theta\,\vec{k}_0.\\ & \vec{v}^{\,A}_{21} = 2R\dot{\phi}\,\vec{\jmath}_0. \\ & \vec{\omega}_{21}\times\overrightarrow{AG} = -R\dot{\theta}\cos\theta\,\vec{\imath}_0 - R\dot{\phi}\mathrm{sen}\theta\,\vec{\jmath}_0 - R\dot{\theta}\mathrm{sen}\theta\,\vec{k}_0.\\ & \qquad\overrightarrow{AG} = R\,\vec{\jmath}_2 = -R\,\mathrm{sen}\theta\,\vec{\imath}_0 + \cos\theta\,\vec{k}_0. \end{array} }

La cantidad de movimiento es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{C}_2 = -mR\dot{\theta}\cos\theta\,\vec{\imath}_0 - mR\dot{\phi}(2-\mathrm{sen}\theta)\,\vec{\jmath}_0 - mR\dot{\theta}\mathrm{sen}\theta\,\vec{k}_0. }