Diferencia entre revisiones de «Descenso en un proceso cíclico»
Sin resumen de edición |
|||
| Línea 97: | Línea 97: | ||
|} | |} | ||
</center> | </center> | ||
==Representación gráfica== | |||
En este proceso solo podemos representar los procesos B→C y D→A, que son los únicos cuasiestáticos. Al ser procesos a presión constante, se representan por segmentos horizontales en un diagrama pV. Los procesos adiabáticos no los podemos representar por no ser cuasiestáticos, aunque sí podemos marcar los estados inicial y final de cada uno. | |||
==Trabajo y calor== | |||
===Proceso A→B=== | |||
Este proceso es adiabático, por lo que | |||
<center><math>Q_{A\to B} = 0\,</math></center> | |||
mientras que el trabajo coincide con la variación de la energía interna, por la misma razón | |||
<center><math>W_{A\to B}= U(B)-U(A)=\frac{p_BV_B-pAV_A}{\gamma-1} = \frac{125\cdot 6.00-100\cdot 7.00}{0.4}\,\mathrm{J}= +125\,\mathrm{J}</math></center> | |||
Este trabajo puede calcularse también como | |||
<center><math>W_{A\to B}=-p_B(V_B-V_A)=-125(6.00-7.00)\mathrm{J}= +125\,\mathrm{J}</math></center> | |||
por ser un proceso a presión externa constante (pero no a presión constante). | |||
===Proceso B→C=== | |||
Este proceso es cuasiestático a presión constante, por lo que el calor coincide con la variación en la entalpía | |||
<center><math>Q_{B\to C} = \Delta H = H(C)-H(B)=\frac{\gamma(p_CV_V-p_BV_B)}{\gamma-1}= \frac{1.4(125\cdot 5.60-125\cdot 6.00)}{0.4}\,\mathrm{J}=-175\,\mathrm{J}</math></center> | |||
mientras que el trabajo coincide con la variación de la energía interna menos el calor | |||
<center><math>W_{B\to C}= \Delta U - \Delta H = +125\,\mathrm{J}</math></center> | |||
siendo | |||
<center><math>\Delta U = \frac{125\cdot 5.60-125\cdot 6.00}{0.4}\,\mathrm{J}=-125\,\mathrm{J}</math></center> | |||
Este cambio es opuesto al del proceso A→B porque el gas vuelve a la temperatura inicial. Por tanto | |||
<center><math>W_{B\to C}= -125\,\mathrm{J}+175\,\mathrm{J}=+ 50\,\mathrm{J}</math></center> | |||
Este trabajo puede calcularse también como | |||
<center><math>W_{B\to C}=-p_C(V_C-V_B)=-125(5.60-6.00)\mathrm{J}= +50\,\mathrm{J}</math></center> | |||
por ser un proceso a presión constante (externa e interna). | |||
===Proceso C→D=== | |||
De nuevo tenemos un proceso adiabático, por lo que | |||
<center><math>Q_{C\to D} = 0\,</math></center> | |||
mientras que el trabajo coincide con la variación de la energía interna | |||
<center><math>W_{C\to D}= \Delta U = U(D)-U(C)=\frac{p_DV_D-p_CV_C}{\gamma-1} = \frac{100\cdot 6.60-125\cdot 5.60}{0.4}\,\mathrm{J}= -100\,\mathrm{J}</math></center> | |||
Este trabajo puede calcularse también como | |||
<center><math>W_{C\to D}=-p_D(V_D-V_C)=-100(6.60-5.60)\mathrm{J}= -100\,\mathrm{J}</math></center> | |||
por ser también un proceso a presión externa constante. | |||
===Proceso D→A=== | |||
Este proceso es cuasiestático a presión constante, por lo que el calor coincide con la variación en la entalpía | |||
<center><math>Q_{D\to A} = \Delta H = H(D)-H(A)=\frac{\gamma(p_AV_A-p_DV_D)}{\gamma-1}= \frac{1.4(100\cdot 7.00-100\cdot 6.60)}{0.4}\,\mathrm{J}=+140\,\mathrm{J}</math></center> | |||
mientras que el trabajo coincide con la variación de la energía interna menos el calor | |||
<center><math>W_{B\to C}= \Delta U - \Delta H = +100\,\mathrm{J}-140\,\mathrm{J}=-40\,\mathrm{J}</math></center> | |||
donde hemos usado que, por volver a la temperatura del estado C | |||
<center><math>\Delta U_{D\to A} = -\Delta U_{C\to D}</math></center> | |||
Este trabajo puede calcularse también como | |||
<center><math>W_{D\to A}=-p_A(V_A-V_D)=-100(7.00-6.60)\mathrm{J}= -40\,\mathrm{J}</math></center> | |||
por ser un proceso a presión constante (externa e interna). | |||
===Resumen=== | |||
Reuniendo todos estos resultados tenemos | |||
<center> | |||
{| class="bordeado" | |||
|- | |||
! Proceso !! <math>W\ (\mathrm{J})</math> !! <math>Q\ (\mathrm{J})</math> | |||
|- | |||
! A→B | |||
| +125 || 0 | |||
|- | |||
! B→C | |||
| +50 || −175 | |||
|- | |||
! C→D | |||
| −100 || 0 | |||
|- | |||
! D→A | |||
| −40 || +140 | |||
|} | |||
</center> | |||
El balance global del proceso es que se ha realizado un trabajo sobre el sistema | |||
<center><math>W= (+125+50-100-40)\,\mathrm{J} = +35\,\mathrm{J}</math></center> | |||
Este trabajo coincide con la pérdida de energía potencial de la pesa, que ha descendido 14 cm (de 70 cm a 56 cm) | |||
<center><math>\Delta E_p = mg (h_C-h_A) = 250\,\mathrm{N}(56\,\mathrm{cm}-70\,\mathrm{cm}) = -35\,\mathrm{J}</math></center> | |||
El calor neto del ciclo es | |||
<center><math>W= (0-175+0+140)\,\mathrm{J} = -35\,\mathrm{J}</math></center> | |||
Este es un calor de salida. Tenemos entonces que, como corresponde a un ciclo en el que entra trabajo y sale calor | |||
<center><math>W_\mathrm{in}=+35\,\mathrm{J}=Q_\mathrm{out}</math></center> | |||
El resultado neto es que al final del ciclo el sistema vuelve al estado inicial, pero 35 J de energía potencial se han disipado en forma de calor. | |||
Revisión del 21:35 29 feb 2024
Enunciado
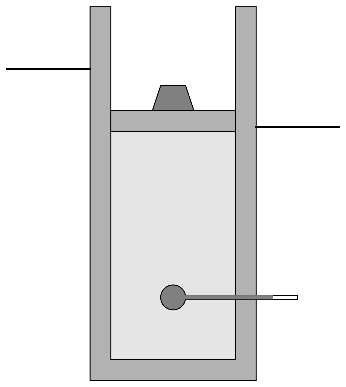
Se construye un sistema de cilindro con pistón, para el cual se sigue el siguiente proceso cíclico. Se parte de un estado A en el que tenemos un cilindro de paredes aisladas térmicamente (aunque el aislante no es perfecto), con pistón. El cilindro tiene 100 cm² de sección y el pistón se halla inicialmente a 70 cm del fondo. El interior del cilindro contiene inicialmente aire seco a 7 ℃ y 100 kPa, que coinciden con la temperatura y la presión del ambiente, las cuales son constantes.
 |
|
| A | B |
|---|---|
 |
|
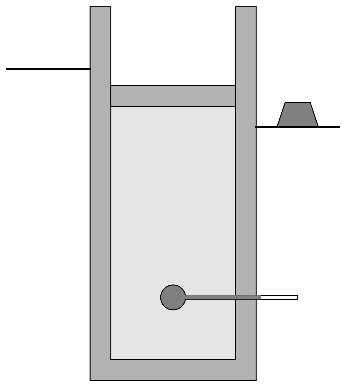
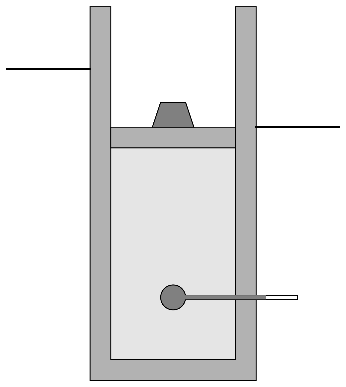
| D | C |
- A→B
- Sobre el pistón se coloca bruscamente una pesa de 250 N, que hace que el pistón descienda una cierta distancia. Este proceso puede suponerse adiabático, pero no cuasiestático.
- B→C
- Sin quitar la pesa se deja que el gas cambie lentamente su temperatura hasta que se iguala a la temperatura exterior.
- C→D
- Se quita bruscamente la pesa a la nueva altura, lo que hace que el pistón suba bruscamente, en otro proceso adiabático no cuasiestático.
- D→A
- Se deja que el aire ceda o absorba calor lentamente hasta que vuelve a estar a la temperatura inicial y en la posición de partida.
Para este ciclo:
- Calcule la presión, temperatura y volumen del aire en cada estado. ¿Cuántos cm desciende la pesa entre los estados A y C?
- Indique gráficamente en un diagrama pV, de manera aproximada, cómo es el ciclo localizando los cuatro estados y trazando aquellos procesos que se puedan representar.
- Calcule el trabajo y el calor que entra en el sistema en cada paso, así como el trabajo neto de entrada y el calor neto de salida en el ciclo.
Presión, volumen y temperatura
Estado A
El estado inicial nos lo da el Enunciado
Estado B
En el primer paso tenemos una compresión adiabática abrupta como en el problema “Compresión adiabática de un gas”. El cálculo es idéntico aquí. El resultado es, para la presión,
para el volumen
y para la temperatura
Vemos que el pistón desciende 10 cm, desde 70 cm a 60 cm mientras la temperatura se incrementa en 20 K.
Estado C
El paso de B a C es una compresión lenta a presión constante, a medida que el calor va escapando por las paredes. En el estado C la presión y temperatura valen
lo que nos da el volumen
La posición del émbolo es ahora a 56 del fondo.
Estado D
Al retirar la pesa se produce una expansión adiabática abrupta. La presión vuelve a ser la inicial
y el volumen se obtiene de manera análoga al paso A→B.
El pistón está ahora a 66 del fondo.
La nueva temperatura es
Durante la expansión adiabática se produce un enfriamiento, pues parte de la energía interna se va en realizar trabajo.
Resumen
Reuniendo todos estos resultados nos queda
| Estado | ||||
|---|---|---|---|---|
| A | 100 | 280 | 7.00 | 70 |
| B | 125 | 300 | 6.00 | 60 |
| C | 125 | 280 | 5.60 | 56 |
| D | 100 | 264 | 6.60 | 66 |
Representación gráfica
En este proceso solo podemos representar los procesos B→C y D→A, que son los únicos cuasiestáticos. Al ser procesos a presión constante, se representan por segmentos horizontales en un diagrama pV. Los procesos adiabáticos no los podemos representar por no ser cuasiestáticos, aunque sí podemos marcar los estados inicial y final de cada uno.
Trabajo y calor
Proceso A→B
Este proceso es adiabático, por lo que
mientras que el trabajo coincide con la variación de la energía interna, por la misma razón
Este trabajo puede calcularse también como
por ser un proceso a presión externa constante (pero no a presión constante).
Proceso B→C
Este proceso es cuasiestático a presión constante, por lo que el calor coincide con la variación en la entalpía
mientras que el trabajo coincide con la variación de la energía interna menos el calor
siendo
Este cambio es opuesto al del proceso A→B porque el gas vuelve a la temperatura inicial. Por tanto
Este trabajo puede calcularse también como
por ser un proceso a presión constante (externa e interna).
Proceso C→D
De nuevo tenemos un proceso adiabático, por lo que
mientras que el trabajo coincide con la variación de la energía interna
Este trabajo puede calcularse también como
por ser también un proceso a presión externa constante.
Proceso D→A
Este proceso es cuasiestático a presión constante, por lo que el calor coincide con la variación en la entalpía
mientras que el trabajo coincide con la variación de la energía interna menos el calor
donde hemos usado que, por volver a la temperatura del estado C
Este trabajo puede calcularse también como
por ser un proceso a presión constante (externa e interna).
Resumen
Reuniendo todos estos resultados tenemos
| Proceso | ||
|---|---|---|
| A→B | +125 | 0 |
| B→C | +50 | −175 |
| C→D | −100 | 0 |
| D→A | −40 | +140 |
El balance global del proceso es que se ha realizado un trabajo sobre el sistema
Este trabajo coincide con la pérdida de energía potencial de la pesa, que ha descendido 14 cm (de 70 cm a 56 cm)
El calor neto del ciclo es
Este es un calor de salida. Tenemos entonces que, como corresponde a un ciclo en el que entra trabajo y sale calor
El resultado neto es que al final del ciclo el sistema vuelve al estado inicial, pero 35 J de energía potencial se han disipado en forma de calor.

































