Diferencia entre revisiones de «Sucesión de tres procesos cuasiestáticos»
Sin resumen de edición |
Sin resumen de edición |
||
| Línea 20: | Línea 20: | ||
mientras que el volumen es el de un cilindro | mientras que el volumen es el de un cilindro | ||
<center><math>V_A = S h = (1001\,\mathrm{cm} | <center><math>V_A = S h = (1001\,\mathrm{cm}^2)(10\mathrm{cm}) = 1000\,\mathrm{cm}^3 = 1.00\,\mathrm{L}</math></center> | ||
===Tras el primer paso=== | ===Tras el primer paso=== | ||
El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el volumen final es el mismo que el inicial | El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el volumen final es el mismo que el inicial | ||
<center><math>V_B = V_A = | <center><math>V_B = V_A = 1.00\,\mathrm{L}</math></center> | ||
La temperatura ha aumentado en 300& | La temperatura ha aumentado en 300 K, | ||
<center><math>T_B = 600\,\mathrm{K}</math></center> | <center><math>T_B = 600\,\mathrm{K}</math></center> | ||
| Línea 46: | Línea 46: | ||
El volumen final lo podemos obtener particularizando la ley de los gases ideales para temperatura constante, es decir, aplicando la ley de Boyle | El volumen final lo podemos obtener particularizando la ley de los gases ideales para temperatura constante, es decir, aplicando la ley de Boyle | ||
<center><math>p_CV_C=p_BV_B\qquad\Rightarrow\qquad V_C = \frac{200\,\mathrm{kPa}}{100\,\mathrm{kPa}} | <center><math>p_CV_C=p_BV_B\qquad\Rightarrow\qquad V_C = \frac{200\,\mathrm{kPa}}{100\,\mathrm{kPa}}1.00\,\mathrm{L} = 2.00\,\mathrm{L}</math></center> | ||
===Estado final=== | ===Estado final=== | ||
| Línea 55: | Línea 55: | ||
La ley de los gases ideales se reduce en este caso a la ley de Charles | La ley de los gases ideales se reduce en este caso a la ley de Charles | ||
<center><math>\frac{V_D}{T_D}=\frac{V_C}{T_C} \qquad\Rightarrow\qquad V_D = \frac{300\,\mathrm{K}}{600\,\mathrm{K}} | <center><math>\frac{V_D}{T_D}=\frac{V_C}{T_C} \qquad\Rightarrow\qquad V_D = \frac{300\,\mathrm{K}}{600\,\mathrm{K}}2.00\,\mathrm{L} = 1.00\,\mathrm{L}</math></center> | ||
Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen. El estado D es el mismo que el estado A y el proceso es por tanto un ciclo. | Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen. El estado D es el mismo que el estado A y el proceso es por tanto un ciclo. | ||
===Representación gráfica=== | ===Representación gráfica=== | ||
[[Archivo:ciclo-tres-pasos.png| | [[Archivo:ciclo-tres-pasos.png|center]] | ||
Gráficamente este proceso se compone de tres tramos: | Gráficamente este proceso se compone de tres tramos: | ||
| Línea 87: | Línea 87: | ||
En nuestro caso | En nuestro caso | ||
<center><math>W^{B\to C} = -( | <center><math>W^{B\to C} = -(200\,\mathrm{kPa})(1.00\,\mathrm{L})\ln(2) = -139\,\mathrm{J}</math></center> | ||
===Compresión isóbara=== | ===Compresión isóbara=== | ||
En el tercer paso, el volumen se reduce a presión constante, lo que da un trabajo equivalente gráficamente al área de un rectángulo | En el tercer paso, el volumen se reduce a presión constante, lo que da un trabajo equivalente gráficamente al área de un rectángulo | ||
<center><math>W^{C\to A} = -\int_C^A p\,\mathrm{d} V = -p_A\int_{V_C}^{V_A} = p_A(V_A-V_C) = | <center><math>W^{C\to A} = -\int_C^A p\,\mathrm{d} V = -p_A\int_{V_C}^{V_A} = p_A(V_A-V_C) = 100(2.00 - 1.00)\,\mathrm{J} = +100\,\mathrm{J}</math></center> | ||
===Trabajo neto=== | ===Trabajo neto=== | ||
| Línea 108: | Línea 108: | ||
siendo la capacidad calorífica molar para el aire aproximadamente igual a la de un gas diatómico | siendo la capacidad calorífica molar para el aire aproximadamente igual a la de un gas diatómico | ||
<center><math>c_v = \frac{ | <center><math>c_v =\frac{R}{\gamma-1} = 20.8\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center> | ||
con <math>\gamma = 1.4</math>. | |||
La variación de la energía interna en cualquier proceso es proporcional a la diferencia de temperaturas | La variación de la energía interna en cualquier proceso es proporcional a la diferencia de temperaturas | ||
| Línea 114: | Línea 116: | ||
<center><math>\Delta U = nc_v\,\Delta T</math></center> | <center><math>\Delta U = nc_v\,\Delta T</math></center> | ||
independientemente de si el proceso es a presión constante, a volumen constante o como sea, por tratarse de una función de estado. | independientemente de si el proceso es a presión constante, a volumen constante o como sea, por tratarse de una función de estado. También se puede calcular a partir de las presiones y volúmenes como | ||
<center><math>\Delta U = \frac{p_fV_f-p_iV_i}{\gamma-1}</math></center> | |||
Una vez que calculemos la variación en la energía, podemos hallar el calor que entra en el gas por el primer principio de la termodinámica | Una vez que calculemos la variación en la energía, podemos hallar el calor que entra en el gas por el primer principio de la termodinámica | ||
| Línea 123: | Línea 127: | ||
Al calentarse el gas aumenta su energía interna | Al calentarse el gas aumenta su energía interna | ||
<center><math>\Delta U^{A\to B} | <center><math>\Delta U^{A\to B} = \frac{p_BV_B-p_AV_A}{\gamma-1} = \frac{5}{2}(p_B-p_A)V_A = \frac{5}{2}(200- 100)(1.00)\,\mathrm{J}=+250\,\mathrm{J}</math></center> | ||
Puesto que en este proceso el trabajo es nulo, este aumento en la energía procede exclusivamente del calor | Puesto que en este proceso el trabajo es nulo, este aumento en la energía procede exclusivamente del calor | ||
| Línea 159: | Línea 163: | ||
siendo | siendo | ||
<center><math>c_p = \frac{ | <center><math>c_p = \frac{\gamma R}{\gamma-1} = 29.1\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{mol}}</math></center> | ||
Este método nos daría | Este método nos daría | ||
<center><math>Q^{C\to A} = \frac{7}{2}\left(nRT_A-nRT_C\right) = \frac{ | <center><math>Q^{C\to A} = \frac{7}{2}\left(nRT_A-nRT_C\right) = \frac{\gamma(p_AV_A-p_CV_C)}{\gamma-1} = \frac{\gamma p_A(V_A-V_C)}{\gamma-1} = \frac{1.4\cdot 100(1.00-2.00)}{0.4}\,\mathrm{J} = -350\,\mathrm{J}</math></center> | ||
Nótese que para el calor sí se cambia <math>c_v</math> por <math>c_p</math>. | Nótese que para el calor sí se cambia <math>c_v</math> por <math>c_p</math>. | ||
Revisión del 20:46 21 feb 2024
Enunciado
Un cilindro de 100 cm² de sección contiene aire y está cerrado por un émbolo. Inicialmente el aire tiene una temperatura de 27 °C y una presión de 100 kPa, que también es la presión exterior, estando el émbolo a 10 cm del fondo. Entonces se realiza el siguiente proceso cuasiestático
- A→B Se atornilla el émbolo y se calienta el aire hasta 327 °C, sumergiéndolo en un baño a esta temperatura.
- B→C Se libera el émbolo lentamente, dejando que se expanda el aire hasta que su presión vuelve a ser la inicial. En este proceso el aire se mantiene a la temperatura de 327 °C.
- C→A Con el émbolo libre, se enfría gradualmente hasta que la temperatura vuelve a ser la inicial.
Para este proceso:
- Halle la presión, volumen y temperatura al final de cada fase del proceso.
- Calcule el trabajo en cada fase, así como el trabajo neto total.
- Calcule la variación en la energía interna y el calor en cada paso y su variación neta.
Presión, volumen y temperatura
Estado inicial
Inicialmente tenemos que la presión y la temperatura valen
mientras que el volumen es el de un cilindro
Tras el primer paso
El primer paso ocurre a volumen constante, por estar el pistón atornillado, con lo que el volumen final es el mismo que el inicial
La temperatura ha aumentado en 300 K,
y la presión aumenta en la misma proporción que la temperatura
Tras el segundo paso
En el segundo paso tenemos una expansión isoterma, siendo la temperatura final igual a la que había al final del paso anterior
mientras que la presión final vuelve a ser la que había al principio
El volumen final lo podemos obtener particularizando la ley de los gases ideales para temperatura constante, es decir, aplicando la ley de Boyle
Estado final
Por último, dejando el émbolo libre, la temperatura vuelve a ser la inicial, manteniéndose constante la presión
La ley de los gases ideales se reduce en este caso a la ley de Charles
Al ser la presión y la temperatura finales iguales a las de partida también lo es el volumen. El estado D es el mismo que el estado A y el proceso es por tanto un ciclo.
Representación gráfica
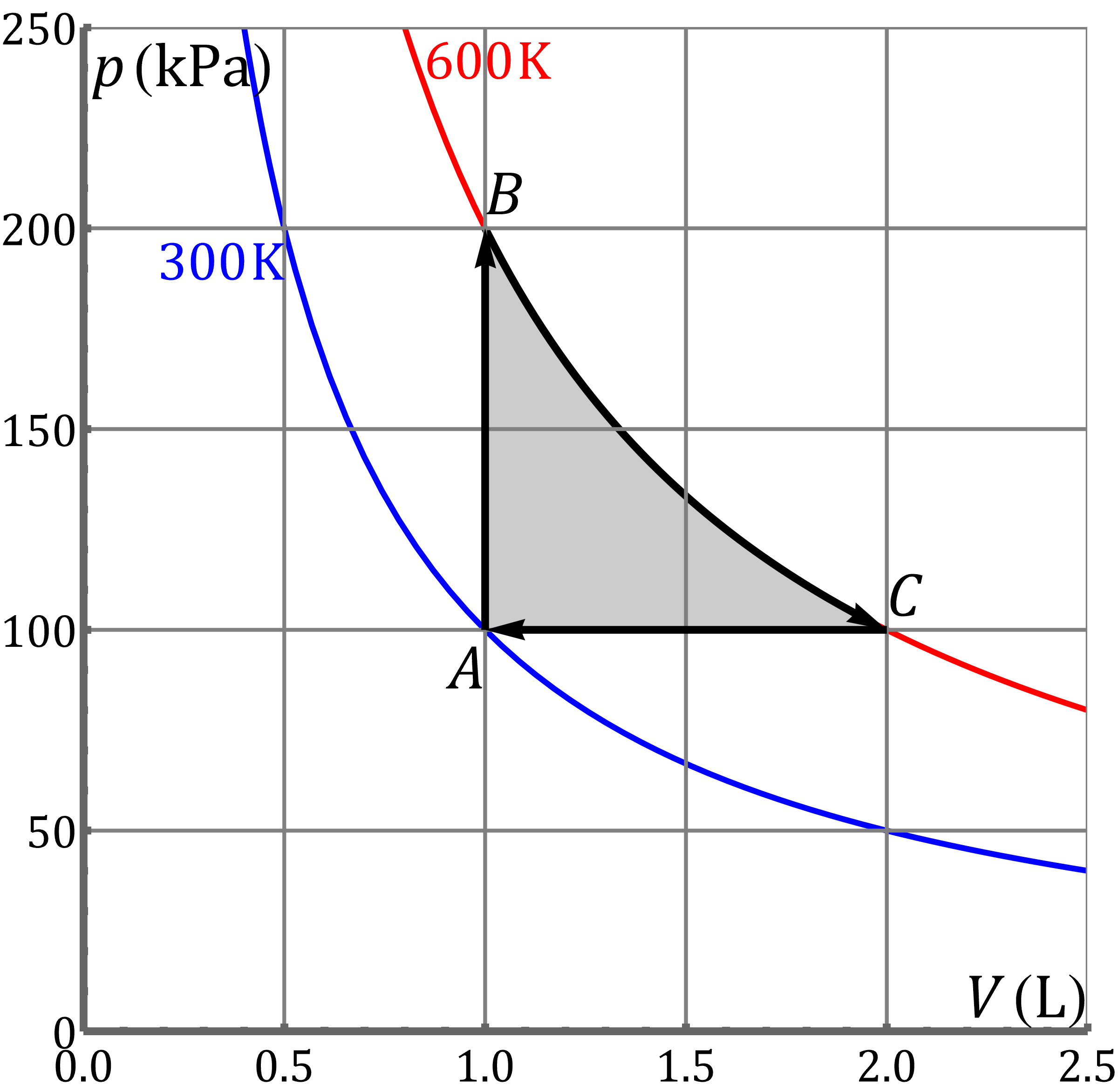
Gráficamente este proceso se compone de tres tramos:
- Un calentamiento a volumen constante, que corresponde a una recta vertical.
- Una expansión isoterma, que se representa por un arco de hipérbola.
- Una compresión a presión constante, que en la gráfica queda como una recta horizontal.
Trabajo
Podemos hallar el trabajo sobre el gas en cada paso a partir de la evolución de sus variables de estado, si suponemos que todos los procesos son cuasiestáticos.
Calentamiento a volumen constante
Al permanecer constante el volumen, no se realiza trabajo sobre el gas
Expansión isoterma
Cuando la temperatura permanece constante, podemos calcular el trabajo con ayuda de la ley de Boyle. En cualquier punto del camino
lo que nos da el trabajo
En nuestro caso
Compresión isóbara
En el tercer paso, el volumen se reduce a presión constante, lo que da un trabajo equivalente gráficamente al área de un rectángulo
Trabajo neto
El trabajo neto sobre el gas en el ciclo será la suma de los trabajos individuales
El signo del trabajo nos dice que en realidad es el gas el que realiza el trabajo sobre el ambiente.
Energía y calor
La energía interna de un gas ideal depende solamente de su temperatura
siendo la capacidad calorífica molar para el aire aproximadamente igual a la de un gas diatómico
con .
La variación de la energía interna en cualquier proceso es proporcional a la diferencia de temperaturas
independientemente de si el proceso es a presión constante, a volumen constante o como sea, por tratarse de una función de estado. También se puede calcular a partir de las presiones y volúmenes como
Una vez que calculemos la variación en la energía, podemos hallar el calor que entra en el gas por el primer principio de la termodinámica
Proceso A→B
Al calentarse el gas aumenta su energía interna
Puesto que en este proceso el trabajo es nulo, este aumento en la energía procede exclusivamente del calor
Este calor se podía haber hallado directamente observando que en un proceso a volumen constante
Proceso B→C
En la expansión isoterma la temperatura permanece constante, y por tanto, también lo es la energía interna
Esto quiere decir que el trabajo que realiza el gas se obtiene a base de absorber calor
Proceso C→A
Por último, en la compresión a presión constante, la temperatura vuelve a su valor inicial, y lo mismo hace la energía interna
Obsérvese que aunque el proceso sea a presión constante, en la expresión de la energía aparece .
El calor en este caso vale
Al tratarse de un proceso a presión constante, el calor puede también hallarse directamente como
siendo
Este método nos daría
Nótese que para el calor sí se cambia por .
Balance
Sumando los tres pasos, obtenemos la variación de energía
que es nula, como corresponde a que el proceso es cíclico y la energía es una función de estado.
Para el calor, en cambio
El resultado neto es que a lo largo del ciclo entran en forma de calor y sale la misma cantidad en forma de trabajo. Este ciclo describiría un modelo muy simple de máquina térmica.




































