Diferencia entre revisiones de «Compresión lineal de un gas»
(Página creada con «==Enunciado== Se comprime cuasiestáticamente un gas ideal que inicialmente se encuentra a presión <math>p_A = 100\,\mathrm{kPa}</math>, temperatura <math>T_A = 300\,\mathrm{K}</math> y ocupa un volumen <math>V_A = 0.01\,\mathrm{m}^3</math>, según la ley <center><math>p = 3p_A-\frac{2p_AV}{V_A}</math></center> La compresión continúa hasta que la presión vale <math>p_B = 2p_A</math>. # Trace la gráfica del proceso en un diagrama PV. # Calcule la temperatura fi…») |
Sin resumen de edición |
||
| Línea 7: | Línea 7: | ||
La compresión continúa hasta que la presión vale <math>p_B = 2p_A</math>. | La compresión continúa hasta que la presión vale <math>p_B = 2p_A</math>. | ||
# Calcule la temperatura final del gas. ¿Es este un proceso isotermo? | |||
# Calcule la temperatura final del proceso | # Trace la curva que describe el proceso en un diagrama pV. | ||
# | # ¿Cuál es la temperatura máxima que alcanza el gas? ¿En qué estado la alcanza? | ||
# | |||
==Temperatura final== | ==Temperatura final== | ||
Si escribimos la ecuación con valores numéricos, con la presión en kPa, la temperatura en K y el volumen en litros tenemos | |||
<center><math> | <center><math>p_A=100\qquad V_A = 10\qquad T_A = 300\qquad\qquad p_B = 2p_A = 200</math></center> | ||
lo que llevado a la ecuación del proceso da | |||
<center><math> | <center><math>p = 300 - \frac{200}{10}V = 300 - 20V</math></center> | ||
El volumen final corresponde al estado en el que la presión vale 200 kPa | |||
== | <center><math>200 = 300 - 20V_B \qquad\Rightarrow\qquad V_B = 5\,\mathrm{L}</math></center> | ||
Obtenemos la temperatura final a partir de la ecuación de los gases ideales. | |||
<center><math> | <center><math>\frac{p_AV_A}{T_A} = \frac{p_BV_B}{T_B}\qquad\Rightarrow\qquad T_B=T_A\,\frac{p_B}{p_A}\,\frac{V_B}{V_A}=300\,\frac{200}{100}\,\frac{5}{10}=300\,\mathrm{K}</math></center> | ||
Vemos que la temperatura final es la misma que la inicial. | |||
Podríamos pensar que se trata de un proceso isotermo, pero no lo es, ya que la temperatura cambia a lo largo del proceso. No basta con que la temperatura en los extremos sea la misma. Debe ser constante en todo el camino. | |||
Analíticamente tenemos para la temperatura en los estados intermedios | |||
<center><math> | <center><math>T = 300\,\frac{p}{100}\,\frac{V}{10}= 300\,\frac{300-20V}{100}\,\frac{V}{10} = 90V-6V^2</math></center> | ||
que no es una constante. | |||
==Representación gráfica== | |||
Dado que la presión depende del volumen en la forma | |||
<center><math> | <center><math>p = 300-20V = a + b V\,</math>{{qquad}}{{qquad}}<math>a = 300\,</math>{{qquad}}{{qquad}}<math>b = -20</math></center> | ||
es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es <math>(10,300)</math> y el punto final corresponde a <math>(5,200)</math> | |||
<center> | <center>[[Archivo:calentamiento-lineal.png]]</center> | ||
Si fuera un proceso isotermo, la curva debería ser una hipérbola. Si trazamos la gráfica del proceso y de las isotermas, vemos que la temperatura inicialmente aumenta y luego disminuye. | |||
==Temperatura máxima== | ==Temperatura máxima== | ||
Antes hemos calculado la temperatura para cada volumen | |||
<center><math>T | <center><math>T = 90V-6V^2\,</math></center> | ||
La gráfica de esta función tiene una forma parabólica, con un máximo en algún punto intermedio entre el estado inicial y el final. Hallamos la posición del máximo igualando la derivada a cero. | La gráfica de esta función tiene una forma parabólica, con un máximo en algún punto intermedio entre el estado inicial y el final. Hallamos la posición del máximo igualando la derivada a cero. | ||
<center><math>0 = \frac{\mathrm{d}T}{\mathrm{d}V}=\ | <center><math>0 = \frac{\mathrm{d}T}{\mathrm{d}V}=90-12V\qquad\Rightarrow\qquad V = \frac{90}{12}=7.5\,\mathrm{L}</math></center> | ||
Este volumen corresponde al punto medio entre el estado inicial y el final. La temperatura en este punto es | Este volumen corresponde al punto medio entre el estado inicial y el final. La temperatura en este punto es | ||
<center><math>T_\mathrm{max}=\ | <center><math>T_\mathrm{max}=90\cdot 7.5-6\cdot(7.5)^2 = 337.5\,\mathrm{K}</math></center> | ||
Revisión del 11:13 17 feb 2024
Enunciado
Se comprime cuasiestáticamente un gas ideal que inicialmente se encuentra a presión , temperatura y ocupa un volumen , según la ley
La compresión continúa hasta que la presión vale .
- Calcule la temperatura final del gas. ¿Es este un proceso isotermo?
- Trace la curva que describe el proceso en un diagrama pV.
- ¿Cuál es la temperatura máxima que alcanza el gas? ¿En qué estado la alcanza?
Temperatura final
Si escribimos la ecuación con valores numéricos, con la presión en kPa, la temperatura en K y el volumen en litros tenemos
lo que llevado a la ecuación del proceso da
El volumen final corresponde al estado en el que la presión vale 200 kPa
Obtenemos la temperatura final a partir de la ecuación de los gases ideales.
Vemos que la temperatura final es la misma que la inicial.
Podríamos pensar que se trata de un proceso isotermo, pero no lo es, ya que la temperatura cambia a lo largo del proceso. No basta con que la temperatura en los extremos sea la misma. Debe ser constante en todo el camino.
Analíticamente tenemos para la temperatura en los estados intermedios
que no es una constante.
Representación gráfica
Dado que la presión depende del volumen en la forma
es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es y el punto final corresponde a
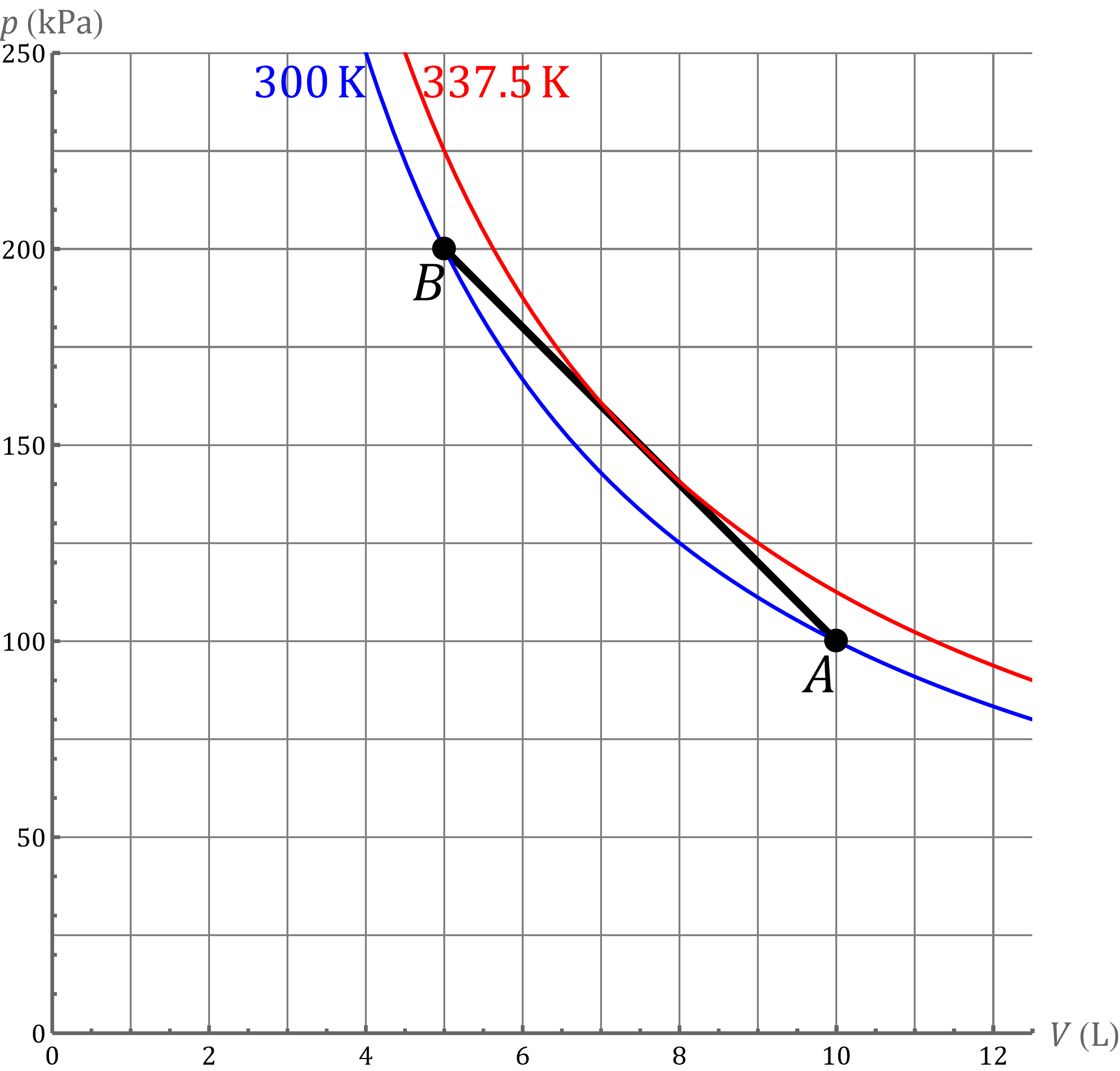
Si fuera un proceso isotermo, la curva debería ser una hipérbola. Si trazamos la gráfica del proceso y de las isotermas, vemos que la temperatura inicialmente aumenta y luego disminuye.
Temperatura máxima
Antes hemos calculado la temperatura para cada volumen
La gráfica de esta función tiene una forma parabólica, con un máximo en algún punto intermedio entre el estado inicial y el final. Hallamos la posición del máximo igualando la derivada a cero.
Este volumen corresponde al punto medio entre el estado inicial y el final. La temperatura en este punto es

















