Partícula en aro con diferentes métodos (MRGIC)

Enunciado

Partícula en aro con diferentes métodos

Se tiene un aro circular de radio $R$ contenido en un plano vertical. Engarzado en él hay una masa $m$ que puede deslizar siguiendo la circunferencia del aro bajo la acción de la gravedad.

1. Suponiendo que el contacto es liso, encuentra las ecuación de movimiento de la masa usando el Principio de D'Alembert.
2. Repite el primer apartado usando la energía cinética y fuerzas generalizadas.
3. Repite el primer apartado usando la Función de Lagrange.
4. Repite el primer apartado usando el Prinicipio de Liberación.
5. Repite el primer apartado usando la técnica de los multiplicadores de Lagrange.
6. Consideremos ahora que el vínculo entre la partícula y el aro es rugoso, con un coeficiente de rozamiento dinámico $\mu$. Determina las ecuaciones de movimiento usando el Principio de Liberación.

Solución

Principio de D'Alembert

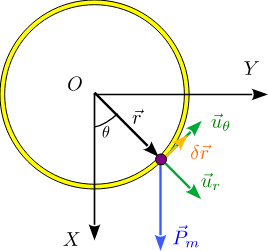
Primero identificamos el número de grados de libertad. La partícula está sometida a dos vínculos. Usando coordenadas cilíndricas estos vínculos se expresan

$r=R,\qquad z=0.$

Por tanto, la partícula tiene un grado de libertad. Vamos a usar la coordenada $\theta$ para trabajar. Los vectores de posición, velocidad y aceleración en coordenadas cilíndricas son

${\begin{array}{l}{\vec {r}}=R\,{\vec {u}}_{r},\\{\vec {v}}=R{\dot {\theta }}\,{\vec {u}}_{\theta },\\{\vec {a}}=-R{\dot {\theta }}^{2}\,{\vec {u}}_{r}+R{\ddot {\theta }}\,{\vec {u}}_{\theta }.\end{array}}$

La única fuerza aplicada es el peso, como se indica en la figura. Proyectándolo cilíndricas tenemos

${\vec {P}}_{m}=mg\cos \theta \,{\vec {u}}_{r}-mg\,\mathrm {sen} \,\theta \,{\vec {u}}_{\theta }.$

El Principio de D'Alembert establece que, en cualquier desplazamiento virtual, debe cumplirse

$({\vec {P}}_{m}-m{\vec {a}})\cdot \delta {\vec {r}}=0.$

Como sólo hay un grado de libertad, el desplazamiento virtual mas general es

$\delta {\vec {r}}=\left({\dfrac {\partial {\vec {r}}}{\partial \theta }}\right)\,\delta \theta =R\,{\dfrac {\partial {\vec {u}}_{r}}{\partial \theta }}\,\delta \theta =R\delta \theta \,{\vec {u}}_{\theta }.$

Recordemos que en coordenadas cilíndricas se tiene

${\dfrac {\partial {\vec {u}}_{r}}{\partial \theta }}={\vec {u}}_{\theta },\qquad {\dfrac {\partial {\vec {u}}_{\theta }}{\partial \theta }}=-{\vec {u}}_{r}.$

Tenemos

${\vec {P}}_{m}-m{\vec {a}}=m(g\cos \theta -R{\dot {\theta }}^{2})\,{\vec {u}}_{r}-m(g\mathrm {sen} \,\theta +R{\ddot {\theta }})\,{\vec {u}}_{\theta }.$

Aplicando el Principio de D'Alembert, obtenemos la ecuación de movimiento

$R{\ddot {\theta }}+g\,\mathrm {sen} \,\theta =0.$

Con la energía cinética

Al haber sólo un grado de libertad, hay una sola ecuación de Lagrange

${\dfrac {\mathrm {d} T}{\mathrm {d} t}}\left({\dfrac {\partial T}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial T}{\partial \theta }}=Q_{\theta }.$

La energía cinética es

$T={\dfrac {1}{2}}m|{\vec {v}}|^{2}={\dfrac {1}{2}}mR^{2}{\dot {\theta }}^{2}.$

Tenemos

${\begin{array}{l}{\dfrac {\partial T}{\partial {\dot {\theta }}}}=mR^{2}{\dot {\theta }}\Rightarrow {\dfrac {\mathrm {d} T}{\mathrm {d} t}}\left({\dfrac {\partial T}{\partial {\dot {\theta }}}}\right)=mR^{2}{\ddot {\theta }},\\{\dfrac {\partial T}{\partial \theta }}=0.\end{array}}$

La fuerza generalizada es debida a la acción del peso. Es decir

$Q_{\theta }={\vec {P}}_{m}\cdot {\dfrac {\partial {\vec {r}}}{\partial \theta }}=-mgR\,\mathrm {sen} \,\theta .$

Finalmente, la ecuación de movimiento es, nuevamente

$R{\ddot {\theta }}+g\,\mathrm {sen} \,\theta =0.$

Con la función de Lagrange

Al ser el peso una fuerza conservativa, podemos asignarle una energía potencial. Tomando como altura de referencia el centro del aro, tenemos

$U=-mgR\cos \theta .$

La función de Lagrange es

$L=T-U={\dfrac {1}{2}}mR^{2}{\dot {\theta }}^{2}+mgR\cos \theta .$

La ecuación de Lagrange es

${\dfrac {\mathrm {d} T}{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial L}{\partial \theta }}=0.$

Tenemos

${\begin{array}{l}{\dfrac {\partial L}{\partial {\dot {\theta }}}}=mR^{2}{\dot {\theta }}\Rightarrow {\dfrac {\mathrm {d} L}{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)=mR^{2}{\ddot {\theta }},\\{\dfrac {\partial L}{\partial \theta }}=-mgR\,\mathrm {sen} \,\theta .\end{array}}$

Por tanto la ecuación de movimiento es, de nuevo

$R{\ddot {\theta }}+g\,\mathrm {sen} \,\theta =0.$

Con el Principio de Liberación

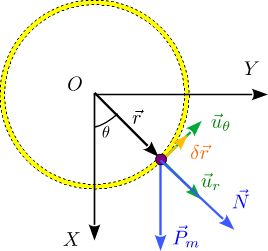
Ahora vamos a romper los vínculos para que vimos en el apartado inicial. De este modo, trabajaremos con las tres coordenadas $\{r,\theta ,z\}$. Ahora bien, por cada vínculo que rompamos, hay que introducir una reacción vincular que, al final, será la que haga que se cumpla el vínculo en el movimiento real. En este caso rompemos dos vínculos relativos a desplazamientos, por lo que hay que añadir dos componentes de fuerza vincular

${\begin{array}{lcl}r=R&\Rightarrow &N_{r}{\vec {u}}_{r}\\z=0&\Rightarrow &N_{z}{\vec {k}}\end{array}}$

La fuerza vincular actúa en la dirección en la que el vínculo restringe el movimiento. Ahora estas fuerzas vinculares se consideran fuerzas activas. Vamos a agrupar las dos fuerzas vinculares en un único vector

${\vec {N}}=N_{r}\,{\vec {u}}_{r}+N_{z}\,{\vec {k}}.$

Para construir la función de Lagrange tenemos que tener en cuenta que ahora todas las coordenadas son libres. Es decir, los vectores de posición y velocidad de la partícula son

${\begin{array}{l}{\vec {r}}=r\,{\vec {u}}_{r}+z\,{\vec {k}},\\{\vec {v}}={\dot {r}}\,{\vec {u}}_{r}+r{\dot {\theta }}\,{\vec {u}}_{\theta }+{\dot {z}}\,{\vec {k}}.\end{array}}$

Las energías cinética y potencial gravitatoria son

${\begin{array}{l}T={\dfrac {m}{2}}\,({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2}),\\U=-mgr\cos \theta .\end{array}}$

La función de Lagrange es

$L=T-U={\dfrac {m}{2}}\,({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2})+mgr\cos \theta .$

Las tres ecuaciones de Lagrange son

${\begin{array}{l}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {r}}}}\right)-{\dfrac {\partial L}{\partial r}}=Q_{r}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial L}{\partial \theta }}=Q_{\theta }^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {z}}}}\right)-{\dfrac {\partial L}{\partial z}}=Q_{z}^{NC}.\end{array}}$

Las fuerzas generalizadas son debidas a las fuerzas vinculares

${\begin{array}{l}Q_{r}^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial r}}=N_{r},\\Q_{\theta }^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial \theta }}=0,\\Q_{z}^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial z}}=N_{z}.\end{array}}$

Las ecuaciones de Lagrange resultantes son

${\begin{array}{l}m{\ddot {r}}-mr{\dot {\theta }}^{2}-mg\cos \theta =N_{r},\\mr^{2}{\ddot {\theta }}+2mr{\dot {r}}{\dot {\theta }}+mgr\,\mathrm {sen} \,\theta =0,\\m{\ddot {z}}=N_{z}.\end{array}}$

Tenemos cinco incógnitas: $\{r,\theta ,z,N_{r},N_{z}\}$. Sólo hay tres ecuaciones de Lagrange, una por coordenada. Pero podemos añadir las ecuaciones de los vínculos, así como sus derivadas

${\begin{array}{lll}r=R,&{\dot {r}}=0,&{\ddot {r}}=0,\\z=0,&{\dot {z}}=0,&{\ddot {z}}=0.\end{array}}$

Al aplicar estas ecuaciones en las ecuaciones de Lagrange obtenemos la ecuación de movimiento junto con las fuerzas vinculares

${\begin{array}{l}N_{r}=-m\,(R{\dot {\theta }}^{2}+g\cos \theta ),\\R{\ddot {\theta }}+R\,\mathrm {sen} \,\theta =0,\\N_{z}=0.\end{array}}$

Con multiplicadores de Lagrange

La idea es similar al principio de liberación. Escribimos los vínculos como funciones que se igualan a cero. Y por cada vínculo que se rompe añadimos un multiplicador de Lagrange

${\begin{array}{lcl}f_{1}=r-R=0&\Rightarrow &\lambda _{1},\\f_{2}=z=0&\Rightarrow &\lambda _{2}.\\\end{array}}$

Ahora las incógnitas son $\{r,\theta ,z,\lambda _{1},\lambda _{1}\}$. Las tres ecuaciones de Lagrange para las coordenadas son

${\begin{array}{l}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {r}}}}\right)-{\dfrac {\partial L}{\partial r}}=Q_{r}^{ML},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial L}{\partial \theta }}=Q_{\theta }^{ML},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {z}}}}\right)-{\dfrac {\partial L}{\partial z}}=Q_{z}^{ML}.\end{array}}$

La función de Lagrange del sistema liberado es la misma que en el apartado anterior. La contribución a las fuerzas generalizadas de los multiplicadores son

${\begin{array}{l}Q_{r}^{ML}=\lambda _{1}{\dfrac {\partial f_{1}}{\partial r}}+\lambda _{1}{\dfrac {\partial f_{2}}{\partial r}}=\lambda _{1},\\Q_{\theta }^{ML}=\lambda _{1}{\dfrac {\partial f_{1}}{\partial \theta }}+\lambda _{1}{\dfrac {\partial f_{2}}{\partial \theta }}=0\\Q_{z}^{ML}=\lambda _{1}{\dfrac {\partial f_{1}}{\partial z}}+\lambda _{1}{\dfrac {\partial f_{2}}{\partial z}}=\lambda _{2}.\end{array}}$

Las derivadas de los vínculos se hacen respecto a las coordenadas porque son vínculos geométricos. Si fuesen vínculos cinemáticos se harían respecto a las velocidades, esto es, $\{{\dot {r}},{\dot {\theta }},{\dot {z}}\}$.

Con esto, las ecuaciones de Lagrange quedan

${\begin{array}{l}m{\ddot {r}}-mr{\dot {\theta }}^{2}-mg\cos \theta =\lambda _{1},\\mr^{2}{\ddot {\theta }}+2mr{\dot {r}}{\dot {\theta }}+mgr\,\mathrm {sen} \,\theta =0,\\m{\ddot {z}}=\lambda _{2}.\end{array}}$

Y ahora aplicamos de nuevo las relaciones vinculares y sus derivadas, con lo que tenemos cinco ecuaciones para cinco incógnitas

${\begin{array}{lll}r=R,&{\dot {r}}=0,&{\ddot {r}}=0,\\z=0,&{\dot {z}}=0,&{\ddot {z}}=0.\end{array}}$

Con esto las ecuaciones de Lagrange quedan

${\begin{array}{l}\lambda _{1}=-m\,(R{\dot {\theta }}^{2}+g\cos \theta ),\\R{\ddot {\theta }}+R\,\mathrm {sen} \,\theta =0,\\\lambda _{2}=0.\end{array}}$

La segunda ecuación es la ecuación de movimiento. La segunda y la tercera dan el valor de los multiplicadores. Si comparamos con las ecuaciones finales del apartado anterior, vemos que

$\lambda _{1}=N_{r},\qquad \lambda _{2}=N_{z}.$

Los multiplicadores son reacciones vinculares aplicadas en el el espacio de las configuraciones, en este caso el formado por las coordenadas $\{r,\theta ,z\}$.

Rozamiento

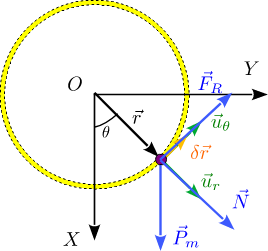
La idea es incluir el rozamiento como una fuerza aplicada. Vamos a hacerlo con el Principio de Liberación. Estamos en régimen de rozamiento dinámico. Entonces la fuerza de rozamiento se opone a la velocidad de deslizamiento de la partícula sobre el vínculo (en este caso el aro) y su módulo es conocido

$|{\vec {F}}_{R}|=\mu |{\vec {N}}|,$

siendo $\mu$ el coeficiente de rozamiento dinámico. La figura de la derecha corresponde al caso en que la partícula está bajando, es decir, ${\dot {\theta }}<0$. Podemos escribir el vector fuerza de rozamiento así

${\vec {F}}_{R}=-\mathrm {sig} (\theta )\mu |{\vec {N}}|{\vec {u}}_{\theta }.$

La función $\mathrm {sig} (\theta )$ es

$\mathrm {sig} (\theta )=\left\{{\begin{array}{rl}1&{\dot {\theta }}>0,\\-1&{\dot {\theta }}<0\end{array}}\right.$

Podemos reutilizar las ecuaciones obtenidas en el apartado de resolución con el Principio de Liberación. La función de Lagrange es

$L=T-U={\dfrac {m}{2}}\,({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+{\dot {z}}^{2})+mgr\cos \theta .$

Las tres ecuaciones de Lagrange son

${\begin{array}{l}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {r}}}}\right)-{\dfrac {\partial L}{\partial r}}=Q_{r}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {\theta }}}}\right)-{\dfrac {\partial L}{\partial \theta }}=Q_{\theta }^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {z}}}}\right)-{\dfrac {\partial L}{\partial z}}=Q_{z}^{NC}.\end{array}}$

Las fuerzas generalizadas son debidas a las fuerzas vinculares y la fuerza de rozamiento

${\begin{array}{l}Q_{r}^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial r}}+{\vec {F}}_{R}\cdot {\dfrac {\partial {\vec {r}}}{\partial r}}=N_{r},\\Q_{\theta }^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial \theta }}+{\vec {F}}_{R}\cdot {\dfrac {\partial {\vec {r}}}{\partial \theta }}=-\mathrm {sig} (\theta )\mu \,r\,{\sqrt {N_{r}^{2}+N_{z}^{2}}},\\Q_{z}^{NC}={\vec {N}}\cdot {\dfrac {\partial {\vec {r}}}{\partial z}}+{\vec {F}}_{R}\cdot {\dfrac {\partial {\vec {r}}}{\partial z}}=N_{z}.\end{array}}$

Tenemos cinco incógnitas: $\{r,\theta ,z,N_{r},N_{z}\}$. Sólo hay tres ecuaciones de Lagrange, una por coordenada. Pero podemos añadir las ecuaciones de los vínculos, así como sus derivadas

${\begin{array}{lll}r=R,&{\dot {r}}=0,&{\ddot {r}}=0,\\z=0,&{\dot {z}}=0,&{\ddot {z}}=0.\end{array}}$

Al aplicar estas ecuaciones en las ecuaciones de Lagrange obtenemos la ecuación de movimiento junto con las fuerzas vinculares

${\begin{array}{l}N_{r}=-m\,(R{\dot {\theta }}^{2}+g\cos \theta ),\\R{\ddot {\theta }}+R\,\mathrm {sen} \,\theta =-\mathrm {sig} (\theta )\mu \,|R{\dot {\theta }}^{2}+g\cos \theta |,\\N_{z}=0.\end{array}}$

Debido a la presencia de la función signo y el valor absoluto en la ecuación de movimiento, a la hora de integrar las ecuaciones hay que considerar separadamente los casos ${\dot {theta}}>0$ y ${\dot {\theta }}<0$.