Triciclo (MR G.I.C.)

Enunciado

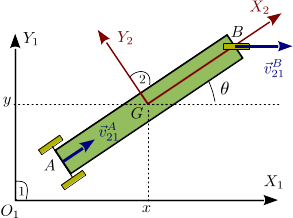
El sistema de la figura representa un modelo muy simple de triciclo. Está formado por una barra homogénea Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overline{AB}} (sólido "2", masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m} , longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle l=2a} , centro de masas $G$) contenida en el plano horizontal $OX_{1}Y_{1}$ y obligada a moverse de modo que su extremo $A$ tiene una velocidad apuntando a $B$, mientras que la velocidad de $B$ se mantiene siempre paralela al eje $OX_{1}$. Se propone trabajar con las coordenadas generalizadas $\{x,y,\theta \}$ indicadas en la figura.

1. Demuestra que las condiciones de movimiento implican las siguientes ecuaciones de ligadura para los puntos $A$ y $B$: $\{a_{1}\operatorname {sen} \theta {\dot {x}}+a_{2}\cos \theta {\dot {y}}+a_{3}{\dot {\theta }}=0;\,b_{1}{\dot {x}}+b_{2}{\dot {y}}+b_{3}{\dot {\theta }}\cos \theta =0\}$, donde $\{a_{i},b_{i}\}$ son constantes a determinar.
2. Desarrolla las ecuaciones de Lagrange con ligaduras correspondientes al sistema mecánico.
3. Calcula los valores de las fuerzas vinculares $\{{\vec {A}},{\vec {B}}\}$ responsables de las ligaduras del primer apartado en función de los multiplicadores de Lagrange del problema.

Solución

Reducción cinemática

El vector rotación es

${\vec {\omega }}_{21}={\dot {\theta }}\,{\vec {k}}.$

La velocidad en el centro de masas $G$ es

${\vec {v}}_{21}^{\,G}={\dot {x}}\,{\vec {\imath }}_{1}+{\dot {y}}\,{\vec {\jmath }}_{1}.$

Ligaduras

La ligadura en el punto $A$ implica que la velocidad ${\vec {v}}_{21}^{\,A}$ tiene que ser paralela al vector ${\overrightarrow {AB}}$. Este vector es

${\overrightarrow {AB}}=2a\cos \theta \,{\vec {\imath }}_{1}+2a\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}.$

Usando el teorema de Chasles a partir de $G$ la velocidad en $A$ es

${\vec {v}}_{21}^{\,A}={\vec {v}}_{21}^{\,G}+{\vec {\omega }}_{21}\times {\overrightarrow {GA}}=({\dot {x}}+a{\dot {\theta }}\mathrm {sen} \,\theta )\,{\vec {\imath }}_{1}+({\dot {y}}-a{\dot {\theta }}\,\mathrm {sen} \,\theta )\,{\vec {\jmath }}_{1},$

donde hemos usado ${\overrightarrow {GA}}=-a\cos \theta \,{\vec {\imath }}_{1}-a\,\mathrm {sen} \,\theta \,{\vec {\jmath }}_{1}$.

Por tanto la ligadura puede aplicarse exigiendo que

${\vec {v}}_{21}^{\,A}\times {\overrightarrow {AB}}={\vec {0}}\Longrightarrow {\dot {x}}\,\mathrm {sen} \,\theta -{\dot {y}}\cos \theta +a{\dot {\theta }}=0.$

Esta es una ligadura cinemática no integragble, es decir, es no holónoma.

La ligadura en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B } implica que

${\vec {v}}_{21}^{\,B}\parallel {\vec {\imath }}_{1}.$

Usando el teorema de Chasles desde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle G } tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,B}_{21} = \vec{v}^{\,G}_{21} + \vec{\omega}_{21}\times\overrightarrow{GB} = (\dot{x} - a\dot{\theta}\mathrm{sen}\,\theta)\,\vec{\imath}_1 + (\dot{y} + a\dot{\theta}\,\mathrm{sen}\,\theta)\,\vec{\jmath}_1, }

donde hemos usado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{GB} = a\cos\theta\,\vec{\imath}_1 + a\,\mathrm{sen}\,\theta\,\vec{\jmath}_1 } .

Entonces

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{v}^{\,B}_{21} \parallel \vec{\imath}_1 \Longrightarrow \dot{y} + a\dot{\theta}\cos\theta = 0. }

Esta ligadura es cinemática integrable, es decir es holónoma.

Como hay dos ligaduras y es un movimiento plano, el sistema tiene sólo un grado de libertad. Lo que es curioso en este problema es, que aunque la ligadura en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A } es, por si sola, no holónoma, combinada con la ligadura en $B$ sí que se puede integrar. Es decir el problema es holónomo. Sin embargo, esta integración es complicada. Por ello, aunque el sistema puede tiene sólo un grado de libertad, vamos a trabajar con las tres coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{x, y, \theta \} } . Usaremos multiplicadores de Lagrange para poder utlizar las dos coordenadas extras respecto al número de grados de libertad.

Función de Lagrange

Energía cinética

Modelando el triciclo como una barra de longitud Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2a } y masa Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m } , su energía cinética es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle T = \dfrac{1}{2}m|\vec{v}^{\,G}_{21}|^2 + \dfrac{1}{2}I|\vec{\omega}_{21}|^2 = \dfrac{1}{2}m\,(\dot{x}^2 + \dot{y}^2) + \dfrac{1}{2}I\dot{\theta}^2. \qquad (I = ma^2/3) }

El peso no afecta en este problema, pues el centro de masas del triciclo no cambia de altura. Por tanto podemos escoger como energía potencial

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle U = 0 }

La función de Lagrange es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle L = T - U = \dfrac{1}{2}m\,(\dot{x}^2 + \dot{y}^2) + \dfrac{1}{2}I\dot{\theta}^2. }

Ecuaciones de Lagrange

Multiplicadores de Lagrange

Por cada vínculo hay que añadir un multiplicador de Lagrange. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lcl} g_1 = \dot{x}\,\mathrm{sen}\,\theta - \dot{y}\cos\theta + a\dot{\theta} = 0 & \Longrightarrow & \mu_1. \\ g_2 = \dot{y} + a\dot{\theta}\cos\theta = 0 & \Longrightarrow & \mu_2. \end{array} }

Ecuaciones

Tenemos una ecuación de Lagrange por cada coordenada. Para $x$ tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{x}}\right)- \dfrac{\partial L}{\partial x} = \mu_1\,\dfrac{\partial g_1}{\partial \dot{x}} + \mu_2\,\dfrac{\partial g_2}{\partial \dot{x}}. }

Las derivadas parciales que introducen los multiplicadores de Lagrange se hacen respecto a la velocidad Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{x} } porque los vínculos son cinemáticos.

La ecuación resultante es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\ddot{x} = \mu_1\,\mathrm{sen}\,\theta \qquad. (1) }

Hacemos lo mismo para la coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle y } . Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{y}}\right)- \dfrac{\partial L}{\partial y} = \mu_1\,\dfrac{\partial g_1}{\partial \dot{y}} + \mu_2\,\dfrac{\partial g_2}{\partial \dot{y}}. }

La ecuación resultante es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\ddot{y} = -\mu_1\cos\theta + \mu_2 \qquad. (2) }

Por último, para la coordenada Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \theta }

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right)- \dfrac{\partial L}{\partial \theta} = \mu_1\,\dfrac{\partial g_1}{\partial \dot{\theta}} + \mu_2\,\dfrac{\partial g_2}{\partial \dot{\theta}}. }

La ecuación resultante es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle I\ddot{\theta} = \mu_1 a + \mu_2 a\cos\theta \qquad. (3) }

Tenemos 5 incógnitas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{x, y, \theta. \mu_1, \mu_2 \} } . Las dos ecuaciones que faltan son los propios vínculos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lr} \dot{x}\,\mathrm{sen}\,\theta - \dot{y}\cos\theta + a\dot{\theta} = 0, & (4) \\ \dot{y} + a\dot{\theta}\cos\theta = 0. & (5) \end{array} }

Resolución usando el Principio de liberación

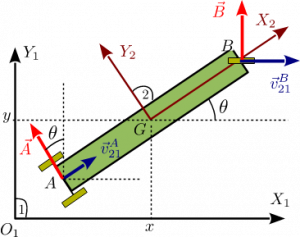
De nuevo vamos a trabajar con las tres coordenadas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \{ x, y, \theta \}, } aunque sólo haya un grado de libertad. Por cada vínculo liberado hay que añadir una reacción vincular. El vínculo en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A } implica que el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle A } no puede moverse dirección perpendicular al vector Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{AB} } . Por tanto, la fuerza víncular que hay que añadir, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{A} } es perpendicular a Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \overrightarrow{AB} } . El vínculo en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle B } prohíbe que este punto se mueva en la dirección del eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1Y_1 } . Es decir, la fuerza vincular ${\vec {B}}$ debe ser paralela al eje Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle O_1Y_1 } , en la dirección del movimiento prohibido. La figura de la derecha muestra las fuerzas vinculares. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{A} = -A\,\mathrm{sen}\,\theta\,\vec{\imath}_1 + A\cos\theta\,\vec{\jmath}_1, \\ \vec{B} = B\,\vec{\jmath}_1. \end{array} }

Ahora las ecuaciones de Lagrange incluyen la contribución de las fuerza vínculares Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{A} } y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{B} } . Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{lcl} \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{x}}\right)- \dfrac{\partial L}{\partial x} & = & Q_x^{NC}, \\ \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{y}}\right)- \dfrac{\partial L}{\partial y} & = & Q_y^{NC}, \\ \dfrac{\mathrm{d} }{\mathrm{d}t}\left(\dfrac{\partial L}{\partial\dot{\theta}}\right)- \dfrac{\partial L}{\partial \theta} & = & Q_{\theta}^{NC}. \end{array} }

El lado izquierdo de estas ecuaciones es igual que el que hemos calculado antes. Lo que cambia son los lados derechos. Para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q^{NC}_x } tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle Q^{NC}_x = \vec{A}\cdot\dfrac{\partial \vec{v}^{\,A}_{21}}{\partial \dot{x}} + \vec{B}\cdot\dfrac{\partial \vec{v}^{\,B}_{21}}{\partial \dot{x}} }