Barra horizontal apoyada en disco

Enunciado

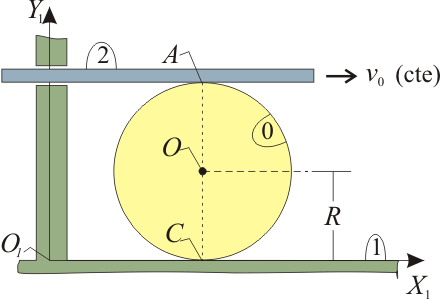
El sistema de la figura consta de un disco (sólido “0”), de centro O y radio $R$, que rueda sin deslizar sobre el eje horizontal $O_{1}X_{1}$ de la escuadra fija $O_{1}X_{1}Y_{1}$ (sólido “1”); y de una barra de longitud indefinida (sólido “2”), que se desplaza horizontalmente con velocidad constante $v_{0}$, manteniéndose siempre en contacto tangente con el perímetro del disco (punto $A$) y sin deslizar sobre éste. Se pide:

1. Reducciones cinemáticas de los movimientos {21}, {01} y {20} en el centro del disco (punto O), es decir: $\{{\vec {\omega }}_{\!21};\,{\vec {v}}_{21}^{\,O}\}$, $\{{\vec {\omega }}_{\,01};\,{\vec {v}}_{\,01}^{\,O}\}$ y $\{{\vec {\omega }}_{\,20};\,{\vec {v}}_{20}^{\,O}\}$.
2. Aceleración relativa barra-disco del punto de contacto $A$, es decir: ${\vec {a}}_{20}^{A}$.

Reducciones cinemáticas

Movimiento {21}

La barra “2” efectúa un movimiento de traslación respecto al sólido “1”, por lo que la velocidad angular de este movimiento es nula y la velocidad de traslación es la misma para todos los puntos, en particular para el punto O.

${\vec {\omega }}_{21}={\vec {0}}\,\,;$      ${\vec {v}}_{21}^{O}=v_{0}{\vec {\imath }}_{1}$

Movimiento {01}

Al ser el contacto entre el disco y el eje horizontal una rodadura sin deslizamiento, el movimiento relativo es una rotación en torno a este punto. Por ello

${\vec {v}}_{01}^{O}=\omega _{01}{\vec {k}}\times {\overrightarrow {CO}}$

La velocidad angular la obtenemos de que podemos hallar la velocidad del punto A, de contacto del disco y la barra, en el movimiento {01}, por ser este contacto también una rodadura sin deslizamiento

${\vec {v}}_{01}^{A}=\overbrace {{\vec {v}}_{02}^{A}} ^{={\vec {0}}}+{\vec {v}}_{21}^{A}=v_{0}{\vec {\imath }}_{1}$

La velocidad de este punto cumple igualmente

${\vec {v}}_{01}^{A}=\omega _{01}{\vec {k}}\times {\overrightarrow {CA}}=\omega _{01}{\vec {k}}\times (2R{\vec {\jmath }}_{1})=-2R\omega _{01}{\vec {\imath }}_{1}$

Igualando las dos expresiones obtenemos la velocidad angular

${\vec {\omega }}_{01}=-{\frac {v_{0}}{2R}}{\vec {k}}$

y la velocidad del punto O

${\vec {v}}_{01}^{O}=-{\frac {v_{0}}{2R}}{\vec {k}}\times (R{\vec {\jmath }}_{1})={\frac {v_{0}}{2}}{\vec {\imath }}_{1}$

Movimiento {20}

Una vez que tenemos dos de las reducciones cinemáticas, podemos hallar la tercera mediante la composición de movimientos. Para la velocidad angular

${\vec {\omega }}_{20}={\vec {\omega }}_{21}+{\vec {\omega }}_{10}=\overbrace {{\vec {\omega }}_{21}} ^{=0}-{\vec {\omega }}_{01}={\frac {v_{0}}{2R}}{\vec {k}}$

y para la lineal

${\vec {v}}_{20}^{O}={\vec {v}}_{21}^{O}+{\vec {v}}_{10}^{O}={\vec {v}}_{21}^{O}-{\vec {v}}_{01}^{O}=v_{0}{\vec {\imath }}_{0}-{\frac {v_{0}}{2}}{\vec {\imath }}_{1}={\frac {v_{0}}{2}}{\vec {\imath }}_{1}$

Aceleración

La aceleración de A la podemos hallar mediante la composición de movimientos

${\vec {a}}_{21}^{A}={\vec {a}}_{20}^{A}+{\vec {a}}_{01}^{A}+2\omega _{01}{\vec {k}}\times {\vec {v}}_{20}^{A}$

de donde, despejando,

${\vec {a}}_{20}^{A}={\vec {a}}_{21}^{A}-{\vec {a}}_{01}^{A}-2\omega _{01}{\vec {k}}\times {\vec {v}}_{20}^{A}$

El movimiento {21} es una traslación a velocidad constante, por lo que la aceleración del punto A en dicho movimiento es nula

${\vec {a}}_{21}^{A}={\frac {\mathrm {d} v_{0}}{\mathrm {d} t}}{\vec {\imath }}_{1}={\vec {0}}$

La aceleración en el movimiento {01} no puede calcularse derivando, porque el punto A es una partícula material diferente en cada instante. Aplicamos la reducción en O del campo de aceleraciones, por ser O un punto material perfectamente definido

${\vec {a}}_{01}^{A}={\vec {a}}_{01}^{O}+\alpha _{01}{\vec {k}}\times {\overrightarrow {OA}}-\omega _{01}^{2}{\overrightarrow {OA}}$

La aceleración de O es nula, por ser el movimiento de este punto rectilíneo y uniforme

${\vec {a}}_{01}^{O}={\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {v_{0}}{2}}{\vec {\imath }}_{1}\right)={\vec {0}}$

También es nula la aceleración angular, por ser la velocidad angular constante

$\alpha _{01}={\frac {\mathrm {d} \omega _{01}}{\mathrm {d} t}}={\frac {\mathrm {d} \ }{\mathrm {d} t}}\left(-{\frac {v_{0}}{2R}}\right)=0$

Queda solo el último término

${\vec {a}}_{01}^{A}=-\omega _{01}^{2}{\overrightarrow {OA}}=-{\frac {v_{0}^{2}}{4R}}{\vec {\jmath }}_{1}$

El término de Coriolis se anula, por ser el contacto una rodadura sin deslizamiento en ese punto

$2\omega _{01}{\vec {k}}\times {\vec {v}}_{20}^{A}=-{\frac {v_{0}}{R}}{\vec {k}}\times {\vec {0}}={\vec {0}}$

lo que nos deja finalmente con

${\vec {a}}_{20}^{A}=-{\vec {a}}_{01}^{A}={\frac {v_{0}^{2}}{4R}}{\vec {\jmath }}_{1}$