Movimiento del gancho de una grúa

Enunciado

El movimiento del gancho de una grúa se puede describir empleando tres coordenadas: su altura $z$ respecto al suelo, la distancia $\rho$ del carro al mástil de la grúa, y el ángulo $\varphi$ que gira la pluma alrededor del mástil. En un momento dado se conocen los valores de estas tres coordenadas ($\rho$, $\varphi$, $z$), así como los de sus derivadas primeras (${\dot {\rho }}$, ${\dot {\varphi }}$, ${\dot {z}}$) y segundas (${\ddot {\rho }}$, ${\ddot {\varphi }}$, ${\ddot {z}}$) respecto al tiempo. Con esta información, determine la velocidad y aceleración del gancho respecto al suelo.

Introducción

Este problema ilustra el uso de las llamadas coordenadas cilíndricas, así como de las coordenadas polares, que son una particularización de éstas para el caso bidimensional. Aunque obtendremos los resultados en el contexto del movimiento relativo de las diferentes partes de una grúa, las expresiones resultantes son aplicables en general.

Tenemos aquí cuatro sólidos:

El mástil “1”

Es la columna que soporta al resto de la estructura.

La pluma o flecha “2”

Es la estructura horizontal sujeta al mástil.

El carro “3”

Es la estructura que se desliza sobre la pluma.

El gancho “4”

es el extremo del cable que pende del carro.

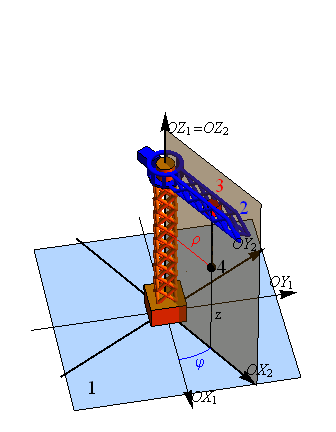
Como sistema de ejes en el que expresar los diferentes vectores consideraremos uno ligado a la pluma (sólido “2”). Los elementos de este sistema son

Origen O

El punto donde el mástil se apoya en el suelo (plano $z=0$).

Eje OZ₂

El definido por el mástil.

Eje OX₂

Uno paralelo a la pluma contenido en el plano $z=0$ (y que por tanto gira como la pluma en torno al mástil).

Eje OY₂

El ortogonal a los dos anteriores, con la orientación dada por la regla de la mano derecha.

El movimiento general del gancho se puede escribir por tanto, como una composición de tres movimientos elementales:

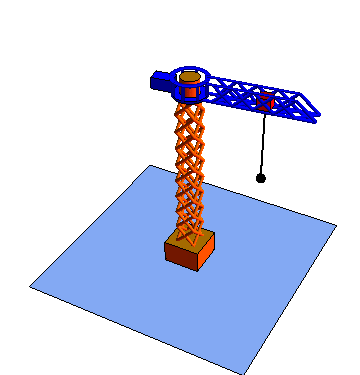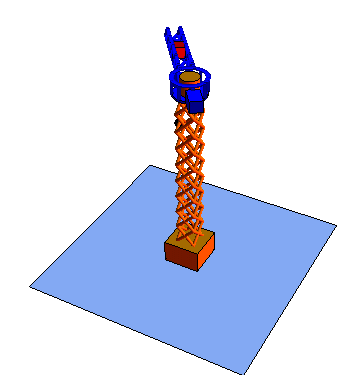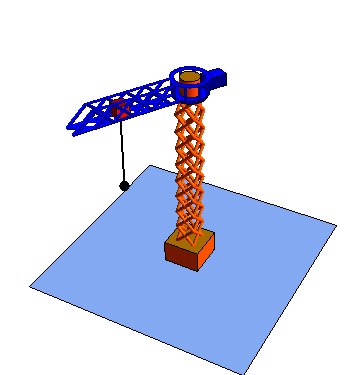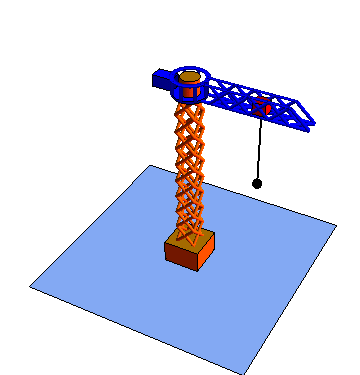
Movimiento {21}

La pluma rota en torno al mástil.

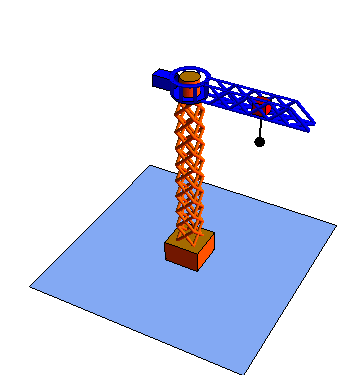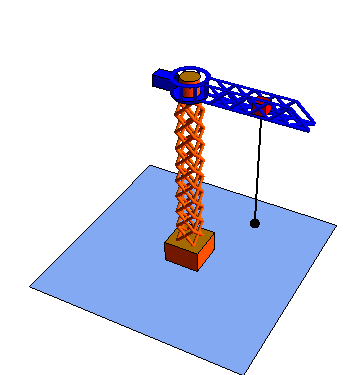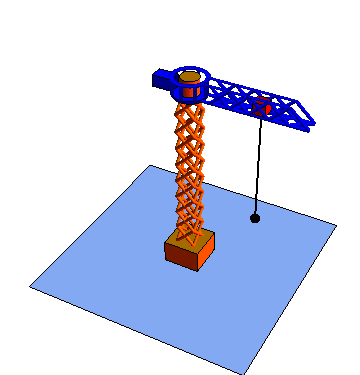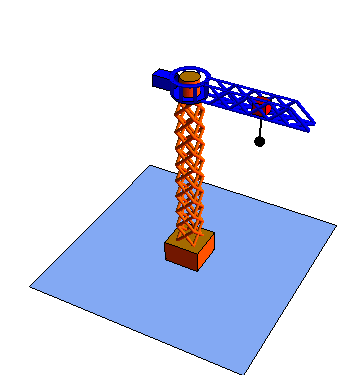
Movimiento {32}

El carro se traslada horizontalmente sobre la pluma.

Movimiento {43}

El gancho se traslada verticalmente respecto al carro.

Rotación {21}	Traslación {32}	Traslación {43}

Velocidad

Al tratarse de una composición de tres movimientos, la velocidad del gancho G respecto al suelo se escribirá como la suma

$\{41\}=\{43\}+\{32\}+\{21\}\,\,\,\,\,$ ⇒ $\,\,\,\,\,{\vec {v}}_{41}^{G}={\vec {v}}_{43}^{G}+{\vec {v}}_{32}^{G}+{\vec {v}}_{21}^{G}$

Sin embargo, a la hora de abordar un problema donde hay más de tres sólidos implicados, la mejor estrategia consiste no en componerlos todos a la vez, sino en irlos componiendo progresivamente, de forma que calculamos la velocidad en varias etapas. En este caso, podemos hallarla como

$\{41\}=(\{43\}+\{32\})+\{21\}=\{42\}+\{21\}\,\,\,\,\,$ ⇒ $\,\,\,\,\,\left\{{\begin{array}{lcr}{\vec {v}}_{41}^{G}&=&{\vec {v}}_{42}^{G}+{\vec {v}}_{21}^{G}\\&&\\{\vec {v}}_{42}^{G}&=&{\vec {v}}_{43}^{G}+{\vec {v}}_{32}^{G}\end{array}}\right.$

También es conveniente tomar nota de los resultados intermedios, pues suelen ser necesarios más tarde.

Tenemos entonces que la velocidad de G respecto al suelo puede hallarse mediante la suma instantánea

${\vec {v}}_{41}^{G}={\vec {v}}_{42}^{G}+{\vec {v}}_{21}^{G}$

El movimiento {21} es una rotación alrededor del eje OZ como eje permanente. La velocidad del punto G en este movimiento es

${\vec {v}}_{21}^{G}={\vec {\omega }}_{21}\times {\overrightarrow {OG}}$

La velocidad angular de este movimiento la da la derivada temporal del ángulo que gira la pluma

${\vec {\omega }}_{21}={\dot {\varphi }}{\vec {k}}_{2}$

Por su parte, la posición del gancho respecto al origen se encuentra contenida en el plano $OX_{2}Z_{2}$, a una distancia $\rho$ y a una altura $z$

${\overrightarrow {OG}}=\rho {\vec {\imath }}_{2}+z{\vec {k}}_{2}$

Resulta la velocidad

${\vec {v}}_{21}^{G}=({\dot {\varphi }}{\vec {k}}_{2})\times (\rho {\vec {\imath }}_{2}+z{\vec {k}}_{2})=\rho {\dot {\varphi }}{\vec {\jmath }}_{2}$

Alternativamente, podíamos haber hallado esta velocidad observando que en un movimiento de rotación la celeridad de cada punto es igual al producto de la velocidad angular por la distancia al eje instantáneo de rotación, y su dirección y sentido vienen dados por la regla de la mano derecha.

El movimiento {42} por su parte es la composición de los movimientos {43} y {32}. Estos dos movimientos elementales son traslaciones paralelas a los ejes, con velocidades

${\vec {v}}_{43}^{G}={\dot {z}}{\vec {k}}_{2}\,\,;$    ${\vec {v}}_{32}^{G}={\dot {\rho }}{\vec {\imath }}_{2}$

La composición de ellos es otra traslación, siendo su velocidad la suma de las dos anteriores

${\vec {v}}_{42}^{G}={\vec {v}}_{43}^{G}+{\vec {v}}_{32}^{G}={\dot {z}}{\vec {k}}_{2}+{\dot {\rho }}{\vec {\imath }}_{2}$

Sumando esta expresión a la hallada anteriormente obtenemos la velocidad del gancho respecto al suelo.

${\vec {v}}_{41}^{G}={\vec {v}}_{42}^{G}+{\vec {v}}_{21}^{G}={\dot {\rho }}{\vec {\imath }}_{2}+\rho {\dot {\varphi }}{\vec {\jmath }}_{2}+{\dot {z}}{\vec {k}}_{2}$

Aceleración

La aceleración la calculamos de manera parecida. De la composición de {42} con {21} tenemos

${\vec {a}}_{41}^{G}={\vec {a}}_{42}^{G}+{\vec {a}}_{21}^{G}+2{\vec {\omega }}_{21}\times {\vec {v}}_{42}^{G}$

La aceleración en el movimiento {21} es la correspondiente a una rotación alrededor del eje OZ.

${\vec {a}}_{21}^{G}=\overbrace {{\vec {a}}_{21}^{O}} ^{={\vec {0}}}+{\vec {\alpha }}_{21}\times {\overrightarrow {OG}}+{\vec {\omega }}_{21}\times ({\vec {\omega }}_{21}\times {\overrightarrow {OG}})$

La aceleración angular de este movimiento es

${\vec {\alpha }}_{21}={\ddot {\varphi }}{\vec {k}}$

lo que nos da la aceleración

${\vec {a}}_{21}^{G}=({\ddot {\varphi }}{\vec {k}}_{2})\times (\rho {\vec {\imath }}_{2}+z{\vec {k}}_{2})+({\dot {\varphi }}{\vec {k}}_{2})\times \left(({\dot {\varphi }}{\vec {k}}_{2})\times (\rho {\vec {\imath }}_{2}+z{\vec {k}}_{2})\right)=-\rho {\dot {\varphi }}^{2}{\vec {\imath }}_{2}+\rho {\ddot {\varphi }}{\vec {\jmath }}_{2}$

El término de Coriolis en la expresión de arriba implica el producto de dos cantidades que ya calculamos previamente

$2{\vec {\omega }}_{21}\times {\vec {v}}_{42}^{G}=2({\dot {\varphi }}{\vec {k}}_{2})\times ({\dot {\rho }}{\vec {\imath }}_{2}+{\dot {z}}{\vec {k}}_{2})=2{\dot {\rho }}{\dot {\varphi }}{\vec {\jmath }}_{2}$

La aceleración en el movimiento {42} se obtiene según la fórmula de Coriolis correspondiente

${\vec {a}}_{42}^{G}={\vec {a}}_{43}^{G}+{\vec {a}}_{32}^{G}+2{\vec {\omega }}_{32}\times {\vec {v}}_{43}^{G}$

Al tratarse el movimiento {32} de una traslación, su velocidad angular es nula, lo que elimina el término de Coriolis. Las dos aceleraciones lineales valen, respectivamente

${\vec {a}}_{43}^{G}={\ddot {z}}{\vec {k}}_{2}\,\,;$    ${\vec {a}}_{32}^{G}={\ddot {\rho }}{\vec {\imath }}_{2}$

y resulta la aceleración relativa

${\vec {a}}_{42}^{G}={\ddot {\rho }}{\vec {\imath }}_{2}+{\ddot {z}}{\vec {k}}_{2}$

Sumando todos los términos llegamos a la expresión para la aceleración del gancho respecto al suelo

${\vec {a}}_{41}^{G}=({\ddot {\rho }}{\vec {\imath }}_{2}+{\ddot {z}}{\vec {k}}_{2})+(-\rho {\dot {\varphi }}^{2}{\vec {\imath }}_{2}+\rho {\ddot {\varphi }}{\vec {\jmath }}_{2})+(2{\dot {\rho }}{\dot {\varphi }}{\vec {\jmath }}_{2})=({\ddot {\rho }}-\rho {\dot {\varphi }}^{2}){\vec {\imath }}_{2}+(\rho {\ddot {\varphi }}+2{\dot {\rho }}{\dot {\varphi }}){\vec {\jmath }}_{2}+{\ddot {z}}{\vec {k}}_{2}$

Coordenadas cilíndricas y polares

Coordenadas cilíndricas

Las variables $\{\rho ,\varphi \,z\}$ que aparecen en este problema poseen una aplicabilidad mucho mayor que la simple descripción del movimiento de una grúa, ya que sirven para identificar cualquier punto del espacio, según las relaciones

$\left\{{\begin{array}{rcl}x&=&\rho \cos(\varphi )\\y&=&\rho \,\mathrm {sen} (\varphi )\\z&=&z\end{array}}\right.$

Lo que hemos obtenido entonces es la expresión de la velocidad y la aceleración de una partícula, cuando su posición se describe mediante coordenadas cilíndricas. Habitualmente, cuando se emplean en este contexto general, a los vectores de la base asociada al sólido 2 se les llama

${\vec {\imath }}_{2}={\vec {u}}_{\rho }\,\,;$    ${\vec {\jmath }}_{2}={\vec {u}}_{\varphi }\,\,;$    ${\vec {k}}_{2}={\vec {u}}_{z}$

por tratarse de los vectores unitarios en las direcciones y sentidos en que aumentan $\rho$, $\varphi$ y $z$, respectivamente. Con esta notación, la posición de una partícula, su velocidad y su aceleración, se escriben empleando coordenadas cilíndricas como

$\left\{{\begin{array}{rcl}{\vec {r}}&=&\rho {\vec {u}}_{\rho }+z{\vec {u}}_{z}\\&&\\{\vec {v}}&=&{\dot {\rho }}{\vec {u}}_{\rho }+\rho {\dot {\varphi }}{\vec {u}}_{\varphi }+{\dot {z}}{\vec {u}}_{z}\\&&\\{\vec {a}}&=&({\ddot {\rho }}-\rho {\dot {\varphi }}^{2}){\vec {u}}_{\rho }+(\rho {\ddot {\varphi }}+2{\dot {\rho }}{\dot {\varphi }}){\vec {u}}_{\varphi }+{\ddot {z}}{\vec {u}}_{z}\end{array}}\right.$

Coordenadas polares

En el caso de que tengamos una partícula moviéndose por un plano, podemos aplicar los resultados anteriores, simplemente considerando que

$z=0\,\,;\qquad {\dot {z}}=0\,\,;\qquad {\ddot {z}}=0$

En este caso las coordenadas cilíndricas se reducen aun sistema de dos coordenadas para el plano, denominadas coordenadas polares. Cumpliéndose las relaciones

$\left\{{\begin{array}{rcl}x&=&\rho \cos(\varphi )\\&&\\y&=&\rho \,\mathrm {sen} (\varphi )\end{array}}\right.$

y siendo las ecuaciones para la posición, velocidad y aceleración de una partícula en el plano

$\left\{{\begin{array}{rcl}{\vec {r}}&=&\rho {\vec {u}}_{\rho }\\&&\\{\vec {v}}&=&{\dot {\rho }}{\vec {u}}_{\rho }+\rho {\dot {\varphi }}{\vec {u}}_{\varphi }\\&&\\{\vec {a}}&=&({\ddot {\rho }}-\rho {\dot {\varphi }}^{2}){\vec {u}}_{\rho }+(\rho {\ddot {\varphi }}+2{\dot {\rho }}{\dot {\varphi }}){\vec {u}}_{\varphi }\end{array}}\right.$

Cuando se usan como coordenadas polares, a la coordenada acimutal $\varphi$ se la suele denotar como $\theta$, con lo que queda

$\left\{{\begin{array}{rcl}x&=&\rho \cos(\theta )\\&&\\y&=&\rho \,\mathrm {sen} (\theta )\end{array}}\right.$            $\left\{{\begin{array}{rcl}{\vec {r}}&=&\rho {\vec {u}}_{\rho }\\&&\\{\vec {v}}&=&{\dot {\rho }}{\vec {u}}_{\rho }+\rho {\dot {\theta }}{\vec {u}}_{\theta }\\&&\\{\vec {a}}&=&({\ddot {\rho }}-\rho {\dot {\theta }}^{2}){\vec {u}}_{\rho }+(\rho {\ddot {\theta }}+2{\dot {\rho }}{\dot {\theta }}){\vec {u}}_{\theta }\end{array}}\right.$