Partícula en barra horizontal con rozamiento (MRGIC)

Enunciado

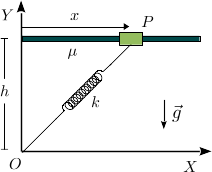
Una partícula $P$ de masa $m$ se ecuentra en un plano vertical y desliza libremente sobre una barra horizontal fija y rugosa (coeficiente dinámico $\mu$) situada en la posición $y=h(cte)$. Un resorte ideal de constante recuperadora $k$ y longitud natural nula tiene uno de sus extremos en $P$ y el otro en el origen de coordenadas $O$. Considera que la partícula se está moviendo hacia la derecha $({\dot {x}}>0)$. Aplica el principio de liberación y, usando los métodos de la Mecánica Analítica, obtén la ecuación diferencial de movimiento de $P$ y el valor de la fuerza normal.

Solución

Una partícula libre tiene tres grados de libertad. En este problema, la partícula debe cumplir dos vínculos

$y=h,\qquad z=0.$

Por tanto, el sistema tiene un grado de libertad. Podemos escoger la coordenada $\{x\}$.

Sin embargo, la presencia del rozamiento hace que no podamos tratar el problema con un sólo grado de libertad. Para poder incluir la fuerza de rozamiento, hay que usar el Principio de liberación, y tratar las fuerzas vinculares (incluida la de rozamiento), como fuerzas activas. Por cada vínculo que rompamos hay que añadir una componente de reacción vincular en la dirección del movimiento afectado por el vínculo. En este caso

${\begin{array}{lcl}y=h&\to &N_{y}\,{\vec {\jmath }},\\z=0&\to &N_{z}\,{\vec {k}}.\end{array}}$

Agrupamos estas dos fuerzas en una sóla fuerza normal

${\vec {N}}=N_{y}\,{\vec {\jmath }}+N_{z}\,{\vec {k}}.$

Como la partícula desliza sobre la barra, estamos en régimen de rozamiento dinámico. En este régimen el módulo de la fuerza de rozamiento es conocido. Su dirección y sentido es opuesto a la velocidad de deslizamiento sobre la barra. Como el problema específica que estudiemos el caso ${\dot {x}}>0$ (movimento hacia la derecha), la fuerza de rozamiento es

${\vec {F}}_{R}=-\mu |{\vec {N}}|\,{\vec {\imath }},$

donde $\mu$ es el coeficiente de rozamiento dinámico entre la partícula y la barra.

El efecto del peso y de la fuerza del muelle se incluyen en la función de Lagrange a través de la energía potencial.

Al aplicar el Principio de liberación, consideramos que el sistema tiene tres grados de libertad $\{x,y,z\}$. Los vectores de posición y velocidad son

${\begin{array}{l}{\vec {r}}=x\,{\vec {\imath }}+y\,{\vec {\jmath }}+z\,{\vec {k}},\\{\vec {v}}={\dot {x}}\,{\vec {\imath }}+{\dot {y}}\,{\vec {\jmath }}+{\dot {z}}\,{\vec {k}},\end{array}}$

La energía cinética es

$T={\dfrac {1}{2}}m|{\vec {v}}|^{2}={\dfrac {1}{2}}m\,({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}).$

Tomamos como referencia la altura del eje $X$ para evaluar la energía pontencial gravitatoria

$U_{g}=mgy$

El muelle tiene longitud natural nula. En la situación liberada, su energía potencial es

$U_{m}={\dfrac {1}{2}}k\,|{\overrightarrow {OP}}|^{2}={\dfrac {1}{2}}\,k\,({x}^{2}+{y}^{2}+{z}^{2}).$

La función de Lagrange es

$L=T-(U_{g}+U_{m})={\dfrac {1}{2}}m\,({\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2})-mgy-{\dfrac {1}{2}}\,k\,({x}^{2}+{y}^{2}+{z}^{2}).$

Las ecuaciones de Lagrange son

${\begin{array}{lcl}{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {x}}}}\right)-{\dfrac {\partial L}{\partial x}}=Q_{x}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {y}}}}\right)-{\dfrac {\partial L}{\partial y}}=Q_{y}^{NC},\\{\dfrac {\mathrm {d} }{\mathrm {d} t}}\left({\dfrac {\partial L}{\partial {\dot {z}}}}\right)-{\dfrac {\partial L}{\partial z}}=Q_{z}^{NC}.\end{array}}$

Las fuerzas generalizadas tiene contibuciones de las fuerzas vincular y de rozamiento.

${\begin{array}{l}Q_{x}^{NC}=({\vec {N}}+{\vec {F}}_{R})\cdot {\dfrac {\partial {\vec {v}}}{\partial {\dot {x}}}}=-\mu \,{\sqrt {N_{y}^{2}+N_{z}^{2}}},\\Q_{y}^{NC}=({\vec {N}}+{\vec {F}}_{R})\cdot {\dfrac {\partial {\vec {v}}}{\partial {\dot {y}}}}=N_{y},\\Q_{z}^{NC}=({\vec {N}}+{\vec {F}}_{R})\cdot {\dfrac {\partial {\vec {v}}}{\partial {\dot {z}}}}=N_{z}.\\\end{array}}$

Después de hacer las derivadas de la función de Lagrange, las ecuaciones de Lagrange quedan

${\begin{array}{lr}m{\ddot {x}}+kx=-\mu {\sqrt {N_{y}^{2}+N_{z}^{2}}},&(1)\\m{\ddot {y}}+ky+mg=N_{y},&(2)\\m{\ddot {z}}+kz=N_{z}.&(3)\end{array}}$

Tenemos cinco incógnitas $\{x,y,z,N_{y},N_{z}\}$. Las dos ecuaciones que faltan son las relaciones vinclares, así como sus derivadas y/o integrales.

${\begin{array}{lllr}y=h,&{\dot {y}}=0,&{\ddot {y}}=0,&(4)\\z=0,&{\dot {z}}=0,&{\ddot {z}}=0.&(5)\end{array}}$

Aplicando las ecuaciones (4)-(5) en (1)-(3) obtenemos

${\begin{array}{l}m{\ddot {x}}+kx=-\mu \,(mg+kh),\\N_{y}=mg+kh,\\N_{z}=0.\end{array}}$