Línea 3:
Línea 3: == Solución ==
== Solución ==
[[Imagen:F1_GIA_p02_01_triangulo.png|right]]
[[Imagen:F1_GIA_p02_01_triangulo.png|right|300px ]]
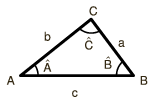
Dado el triángulo de la figura, con lados <math>a</math>, <math>b</math> y <math>c</math> y vértices
Dado el triángulo de la figura, con lados <math>a</math>, <math>b</math> y <math>c</math> y vértices
<math>A</math>, <math>B</math> y <math>C</math>, el teorema del seno relaciona la longitud de los lados
<math>A</math>, <math>B</math> y <math>C</math>, el teorema del seno relaciona la longitud de los lados
Revisión actual - 10:47 26 sep 2023
Enunciado Usando el álgebra vectorial, demuestre el teorema del seno y el teorema del coseno para triángulos planos.
Solución Dado el triángulo de la figura, con lados
a
{\displaystyle a}
b
{\displaystyle b}
c
{\displaystyle c}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
a
s
e
n
A
^
=
b
s
e
n
B
^
=
c
s
e
n
C
^
{\displaystyle {\frac {a}{\,\mathrm {sen} \,{\hat {A}}}}={\frac {b}{\,\mathrm {sen} \,{\hat {B}}}}={\frac {c}{\,\mathrm {sen} \,{\hat {C}}}}}
El teorema del coseno relaciona la longitud de un lado con la longitud
de los otros dos y el coseno del ángulo opuesto,
a
2
=
b
2
+
c
2
−
2
b
c
cos
A
^
b
2
=
a
2
+
c
2
−
2
a
c
cos
B
^
c
2
=
a
2
+
b
2
−
2
a
b
cos
C
^
{\displaystyle {\begin{array}{l}a^{2}=b^{2}+c^{2}-2bc\cos {\hat {A}}\\\\b^{2}=a^{2}+c^{2}-2ac\cos {\hat {B}}\\\\c^{2}=a^{2}+b^{2}-2ab\cos {\hat {C}}\end{array}}}
Teorema del coseno Consideramos los vectores
A
B
→
{\displaystyle {\overrightarrow {AB}}}
A
C
→
{\displaystyle {\overrightarrow {AC}}}
B
C
→
{\displaystyle {\overrightarrow {BC}}}
B
C
→
=
A
C
→
−
A
B
→
{\displaystyle {\overrightarrow {BC}}={\overrightarrow {AC}}-{\overrightarrow {AB}}}
La longitud del lado es
a
=
|
B
C
→
|
{\displaystyle a=|{\overrightarrow {BC}}|}
a
2
=
|
B
C
→
|
2
=
(
A
C
→
−
B
C
→
)
2
=
|
A
C
→
|
2
+
|
B
C
→
|
2
−
2
A
C
→
⋅
A
B
→
=
b
2
+
c
2
−
2
b
c
cos
A
^
{\displaystyle {\begin{array}{ll}a^{2}&=|{\overrightarrow {BC}}|^{2}=({\overrightarrow {AC}}-{\overrightarrow {BC}})^{2}=|{\overrightarrow {AC}}|^{2}+|{\overrightarrow {BC}}|^{2}-2{\overrightarrow {AC}}\cdot {\overrightarrow {AB}}\\&=b^{2}+c^{2}-2bc\cos {\hat {A}}\end{array}}}
pues el ángulo entre
A
C
→
{\displaystyle {\overrightarrow {AC}}}
A
B
→
{\displaystyle {\overrightarrow {AB}}}
A
{\displaystyle A}
Teorema del seno Para demostrar este teorema, utilizamos el producto vectorial de
B
C
→
{\displaystyle {\overrightarrow {BC}}}
B
C
→
×
B
C
→
=
0
→
=
B
C
→
×
(
A
C
→
−
A
B
→
)
⟹
B
C
→
×
A
C
→
=
B
C
→
×
A
B
→
{\displaystyle {\overrightarrow {BC}}\times {\overrightarrow {BC}}={\vec {0}}={\overrightarrow {BC}}\times ({\overrightarrow {AC}}-{\overrightarrow {AB}})\Longrightarrow {\overrightarrow {BC}}\times {\overrightarrow {AC}}={\overrightarrow {BC}}\times {\overrightarrow {AB}}}
Si dos vectores son iguales también lo son sus módulos. Entonces
|
B
C
→
×
A
C
→
|
=
|
B
C
→
×
A
B
→
|
|
B
C
→
|
|
A
C
→
|
s
e
n
C
^
=
|
B
C
→
|
|
A
B
→
|
s
e
n
B
^
a
b
s
e
n
C
^
=
a
c
s
e
n
B
^
b
s
e
n
C
=
c
s
e
n
B
^
b
s
e
n
B
^
=
c
s
e
n
C
^
{\displaystyle {\begin{array}{lll}&|{\overrightarrow {BC}}\times {\overrightarrow {AC}}|=|{\overrightarrow {BC}}\times {\overrightarrow {AB}}|&\\&|{\overrightarrow {BC}}||{\overrightarrow {AC}}|\,\mathrm {sen} \,{\hat {C}}=|{\overrightarrow {BC}}||{\overrightarrow {AB}}|\,\mathrm {sen} \,{\hat {B}}&\\&ab\,\mathrm {sen} \,{\hat {C}}=ac\,\mathrm {sen} \,{\hat {B}}&\\&b\,\mathrm {sen} \,{C}=c\,\mathrm {sen} \,{\hat {B}}&\\&{\frac {\displaystyle b}{\displaystyle \,\mathrm {sen} \,{\hat {B}}}}={\frac {\displaystyle c}{\displaystyle \,\mathrm {sen} \,{\hat {C}}}}\end{array}}}
De nuevo rotando los vectores se obtiene el cociente que falta.
Se puede llegar al mismo resultado observando que el módulo del producto vectorial de dos vectores es
igual al área del triángulo. Así se llega de nuevo a
|
B
C
→
×
A
C
→
|
=
|
B
C
→
×
A
B
→
|
{\displaystyle |{\overrightarrow {BC}}\times {\overrightarrow {AC}}|=|{\overrightarrow {BC}}\times {\overrightarrow {AB}}|}