Diferencia entre revisiones de «Caso de coeficiente de dilatación»
Última edición de la página hace 1 mes por Antonio
| Línea 15: | Línea 15: | ||
Para hallar la derivada calculamos la pendiente de la recta. Tomamos dos puntos de la cuadrícula y resulta | Para hallar la derivada calculamos la pendiente de la recta. Tomamos dos puntos de la cuadrícula y resulta | ||
<center><math>\frac{\Delta\rho}{\Delta T}=\frac{2649-2650}{25-5}\,\frac{\mathrm{kg}}{\mathrm{m}^3 | <center><math>\frac{\Delta\rho}{\Delta T}=\frac{2649-2650}{25-5}\,\frac{\mathrm{kg}}{\mathrm{m}^3{}^\circ{}\mathrm{C}}=-0.2\,\frac{\mathrm{kg}}{\mathrm{m}^3{}^\circ{}\mathrm{C}}</math></center> | ||
lo que nos da el coeficiente de dilatación | lo que nos da el coeficiente de dilatación | ||
<center><math>\beta = -\frac{-0.2}{2650}( | <center><math>\beta = -\frac{-0.2}{2650}({}^\circ\mathrm{C})^{-1}=75\times 10^{-6}({}^\circ\mathrm{C})^{-1}</math></center> | ||
Revisión actual - 09:54 19 feb 2025
Enunciado
En las proximidades de 20℃ la densidad de una sustancia sigue la gráfica lineal de la figura. ¿Cuánto vale el coeficiente de dilatación volumétrica a 20℃, en ?
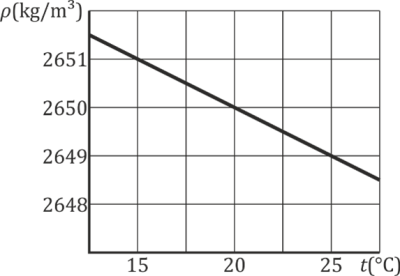
Solución
El coeficiente de dilatación volumétrica se puede calcular de forma aproximada como
A 20℃ el valor de la densidad es
Para hallar la derivada calculamos la pendiente de la recta. Tomamos dos puntos de la cuadrícula y resulta
lo que nos da el coeficiente de dilatación




