Diferencia entre revisiones de «Aro articulado en el extremo de una barra (Jun. 2023)»
| (No se muestran 2 ediciones intermedias del mismo usuario) | |||
| Línea 89: | Línea 89: | ||
</math> | </math> | ||
</center> | </center> | ||
Las reducciones cinemáticas han quedado expresadas en términos de las coordenadas <math>\{\phi, \theta\}</math>. Estos son los dos grados de libertad del sistema de sólidos. | |||
== Cantidad de movimiento y momento angular del aro == | == Cantidad de movimiento y momento angular del aro == | ||
| Línea 179: | Línea 181: | ||
</math> | </math> | ||
</center> | </center> | ||
== Fuerzas y momentos sobre el sistema == | |||
[[Archivo:BarraAroFuerzasSCO2324.png|sinmarco|right|500px]] | |||
Es mejor hacer los dos apartados siguientes a la vez. La única fuerza activa que actúa sobre el sistema es el peso del aro, pues la barra tiene masa nula. El peso se aplica en el centro del aro, su centro de masas. | |||
<center> | |||
<math> | |||
\vec{P}_2 = -mg\,\vec{k}_0. | |||
</math> | |||
</center> | |||
Por otro lado, hay fuerzas y momentos vinculares que actúan sobre el aro y la barra, para garantizar que se cumplan los vínculos. El aro está vinculado con la barra en el punto <math>A</math>. Obtenemos las componentes no nulas de la fuerza y momento vincular que ejerce la barra sobre el aro analizando la reducción cinemática del movimiento {20} en <math>A</math> | |||
<center> | |||
<math> | |||
\begin{array}{lcl} | |||
\vec{v}^{\,A}_{20} = [0, 0, 0]_0 & \to & \vec{A}_{20} = [A_x, A_y, A_z]_0,\\ | |||
\vec{\omega}_{20} = [0, -\dot{\theta}, 0]_0 & \to & \vec{\Gamma}_{20} = [\Gamma_x, 0, \Gamma_z]_0. | |||
\end{array} | |||
</math> | |||
</center> | |||
Así pues, las fuerzas y momentos sobre el aro son <math>\vec{P}_2</math>, <math>\vec{A}_{20}</math> y <math>\vec{\Gamma}_{20}</math>. Están representadas en color rojo en el dibujo de la derecha. Nótese que el momento vincular <math>\vec{\Gamma}_{20}</math> está contenido siempre en el plano <math>OX_0Z_0</math>, mientras que la fuerza vincular <math>\vec{A}_{20}</math> puede apuntar en cualquier dirección. | |||
En lo que respecta a la barra, no hay peso pues su masa es nula. En su extremo $A$ actúan las fuerzas vinculares que son reacciones a las fuerzas vinculares que la barra ejerce sobre el aro (en aplicación de la Tercera Ley de Newton). Por otro lado, la barra "0" está vinculada en el punto <math>O</math>, donde actúan una fuerza y un momento vincular. Tenemos | |||
<center> | |||
<math> | |||
\begin{array}{lcl} | |||
\vec{A}_{02} = -\vec{A}_{20} & \to & \vec{A}_{02} = [-A_x, -A_y, -A_z]_0,\\ | |||
\vec{\Gamma}_{02} = -\vec{\Gamma}_{20} & \to & \vec{A}_{02} = [-\Gamma_x, 0, -\Gamma_z]_0,\\ | |||
\vec{v}^{\,O}_{01} = [0, 0, 0]_0 & \to & \vec{O}_{01} = [O_x, O_y, O_z]_0,\\ | |||
\vec{\omega}_{01} = [0, 0, \dot{\phi}]_0 & \to & \vec{\Lambda}_{01} = [\Lambda_x, \Lambda_y, 0]_0. | |||
\end{array} | |||
</math> | |||
</center> | |||
Estas fuerzas y momentos están dibujados en color verde en la figura. El momento <math>\vec{\Lambda}_{01}</math> está siempre contenido en el plano <math>OX_0Y_0\equiv OX_1Y_1</math>, mientras que la fuerza <math>\vec{O}_{01}</math> puede apuntar en cualquier dirección. | |||
Las incógnitas del problema son los dos grados de libertad que hemos identificado en la reducción cinemática y las componentes de reacciones vinculares que han aparecido | |||
<center> | |||
<math> | |||
\{\phi, \theta, A_x, A_y, A_z, \Gamma_x, \Gamma_z, O_x, O_y, O_z, \Lambda_x, \Lambda_y\} \equiv 12. | |||
</math> | |||
</center> | |||
Hay por tanto doce incógnitas en el problema. | |||
Revisión del 09:50 26 jun 2024
Enunciado
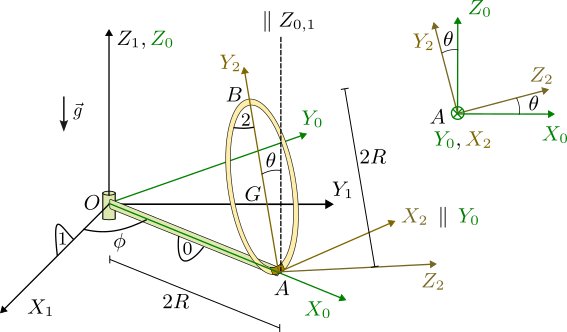
Una barra (sólido "0") homogénea y delgada de longitud y masa despreciable está articulada en el punto fijo . La barra está siempre contenida en el plano y rota alrededor del eje fijo . El sistema de ejes se elige de modo que el eje contenga siempre a la barra. Un aro (sólido "2") de radio y masa , se articula sobre el extremo de la barra "0", de modo que puede rotar alrededor del eje , paralelo en todo momento al eje . El sistema de ejes "2" se elige de modo que sea perpendicular al plano del aro y el eje sea paralelo al . De este modo, el eje contiene siempre al centro del aro y el plano coincide con el plano El aro no rota alrededor del eje . El sistema está sometido a la acción de la gravedad, como se indica en la figura.
Nota: Utiliza la base vectorial asociada al sólido "0" para hacer todos los cálculos.
- Expresa los vectores de la base del sistema "2" en función de los vectores de la base "0", y los de la base "0" en función de los de la base "2".
- Encuentra la reducción cinemática de los movimientos {01}, {20} y {21} en el punto .
- Calcula la cantidad de movimiento del aro y el momento angular del aro en su centro de masas.
- Dibuja el diagrama de fuerzas y momentos sobre la barra y el aro.
- Escribe la expresión genérica de las fuerzas y momentos activos y vinculares que actúan sobre cada sólido. ¿Cuántas incógnitas tiene el problema?
- Escribe la expresión vectorial del T.C.M. y el T.M.C. aplicados a los dos sólidos ¿Cuántas ecuaciones pueden obtenerse? (No hay que escribir las ecuaciones)
- Escribe la energía potencial total del sistema "0" + "2".
- ¿Qué integral o integrales primeras del sistema "0" + "2" existen? ¿Por qué? (No hay que escribir las expresiones).
Supondremos a partir de ahora que la función de Lagrange tiene la forma siendo , y constantes conocidas.
- Aplica el método de los multiplicadores de Lagrange para encontrar las ecuaciones que describen el movimiento de los sólidos si se verifican estas dos ligaduras:
- En tenemos , y . Se aplica una percusión en el punto del aro. Determina el valor de y . (Las ligaduras del apartado anterior no se aplican en este apartado)
Solución
Bases de los sólidos "2" y "0"
Los vectores de la base "2" son
Los vectores de la base "0" son
Reducciones cinemáticas
Para el movimiento {01} tenemos que el eje del movimiento coincide con el eje . Por tanto
Luego nos hará falta la velocidad . Aplicamos la ecuación del campo de velocidades de este movimiento
Para el movimiento {20} vemos que el punto del aro y la barra son siempre el mismo. Además, a partir del dibujo con los ejes "2" y "0", tenemos
Para el movimiento {21} usamos las leyes de composición para la combinación {21} = {20} + {01}. Tenemos
Las reducciones cinemáticas han quedado expresadas en términos de las coordenadas . Estos son los dos grados de libertad del sistema de sólidos.
Cantidad de movimiento y momento angular del aro
La cantidad de movimiento del aro es
Utilizamos la reducción cinemática del movimiento {21} en el punto
La cantidad de movimiento es
Para el momento angular, como se pide en el centro de masas del aro, podemos usar la expresión
Escribimos el tensor de inercia en la base del sólido "2"
con
Para poder hacer el producto escalar tenemos que expresar el vector en la base del sólido "2", la misma base en la que está expresado el tensor de inercia. Usando los resultados del primer apartado tenemos
Finalmente, el momento angular pedido es
Fuerzas y momentos sobre el sistema
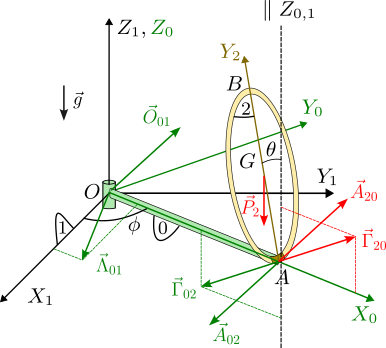
Es mejor hacer los dos apartados siguientes a la vez. La única fuerza activa que actúa sobre el sistema es el peso del aro, pues la barra tiene masa nula. El peso se aplica en el centro del aro, su centro de masas.
Por otro lado, hay fuerzas y momentos vinculares que actúan sobre el aro y la barra, para garantizar que se cumplan los vínculos. El aro está vinculado con la barra en el punto . Obtenemos las componentes no nulas de la fuerza y momento vincular que ejerce la barra sobre el aro analizando la reducción cinemática del movimiento {20} en
Así pues, las fuerzas y momentos sobre el aro son , y . Están representadas en color rojo en el dibujo de la derecha. Nótese que el momento vincular está contenido siempre en el plano , mientras que la fuerza vincular puede apuntar en cualquier dirección.
En lo que respecta a la barra, no hay peso pues su masa es nula. En su extremo $A$ actúan las fuerzas vinculares que son reacciones a las fuerzas vinculares que la barra ejerce sobre el aro (en aplicación de la Tercera Ley de Newton). Por otro lado, la barra "0" está vinculada en el punto , donde actúan una fuerza y un momento vincular. Tenemos
Estas fuerzas y momentos están dibujados en color verde en la figura. El momento está siempre contenido en el plano , mientras que la fuerza puede apuntar en cualquier dirección.
Las incógnitas del problema son los dos grados de libertad que hemos identificado en la reducción cinemática y las componentes de reacciones vinculares que han aparecido
Hay por tanto doce incógnitas en el problema.








































![{\displaystyle {\overset {\leftrightarrow }{I}}_{G}=I_{0}\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/679d32a40abfd06568212d761aef8914c5c394b6)



![{\displaystyle {\vec {L}}_{G}={\overset {\leftrightarrow }{I}}_{G}\cdot {\vec {\omega }}_{21}=I_{0}\left[{\begin{array}{ccc}1&0&0\\0&1&0\\0&0&2\end{array}}\right]_{2}\left[{\begin{array}{c}-{\dot {\theta }}\\{\dot {\phi }}\cos \theta \\{\dot {\phi }}\,\mathrm {sen} \,\theta \end{array}}\right]_{2}=\left[{\begin{array}{c}-I_{0}{\dot {\theta }}\\I_{0}{\dot {\phi }}\cos \theta \\2I_{0}{\dot {\phi }}\,\mathrm {sen} \,\theta \end{array}}\right]_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce3e474f581a47f2e72cfa082efbbd8e6420e01)

![{\displaystyle {\begin{array}{lcl}{\vec {v}}_{20}^{\,A}=[0,0,0]_{0}&\to &{\vec {A}}_{20}=[A_{x},A_{y},A_{z}]_{0},\\{\vec {\omega }}_{20}=[0,-{\dot {\theta }},0]_{0}&\to &{\vec {\Gamma }}_{20}=[\Gamma _{x},0,\Gamma _{z}]_{0}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/657233abbca31506ea81db16aa3c8f81d47fba2a)




![{\displaystyle {\begin{array}{lcl}{\vec {A}}_{02}=-{\vec {A}}_{20}&\to &{\vec {A}}_{02}=[-A_{x},-A_{y},-A_{z}]_{0},\\{\vec {\Gamma }}_{02}=-{\vec {\Gamma }}_{20}&\to &{\vec {A}}_{02}=[-\Gamma _{x},0,-\Gamma _{z}]_{0},\\{\vec {v}}_{01}^{\,O}=[0,0,0]_{0}&\to &{\vec {O}}_{01}=[O_{x},O_{y},O_{z}]_{0},\\{\vec {\omega }}_{01}=[0,0,{\dot {\phi }}]_{0}&\to &{\vec {\Lambda }}_{01}=[\Lambda _{x},\Lambda _{y},0]_{0}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70b71cf4e3a3db000bb2c749e10a9296c11f1915)



