Diferencia entre revisiones de «Proceso formado por dos tramos rectos»
Última edición de la página hace 1 año por Antonio
(Página creada con «==Enunciado== Un gas ideal diatómico experimenta un proceso cuasiestático desde un estado A a un estado B, según la gráfica de la figura center # ¿Cuánto es la variación de la energía interna del gas? # ¿Cuánto calor entra en el gas en este proceso? ==Variación de la energía interna== La variación en la energía interna es <center><math>\Delta U = nc_v\,\Delta T</math></center> Si sustituimos la relación entre la…») |
(→Calor) |
||
| Línea 29: | Línea 29: | ||
<center><math>W = -\int_A^B p\,\mathrm{d}V\qquad\Rightarrow\qquad Q = +\int_A^Bp\,\mathrm{d}V</math></center> | <center><math>W = -\int_A^B p\,\mathrm{d}V\qquad\Rightarrow\qquad Q = +\int_A^Bp\,\mathrm{d}V</math></center> | ||
| |||
<center>[[Archivo:proceso-gas-trapecios.png]]</center> | <center>[[Archivo:proceso-gas-trapecios.png]]</center> | ||
Revisión actual - 20:49 7 mar 2024
Enunciado
Un gas ideal diatómico experimenta un proceso cuasiestático desde un estado A a un estado B, según la gráfica de la figura
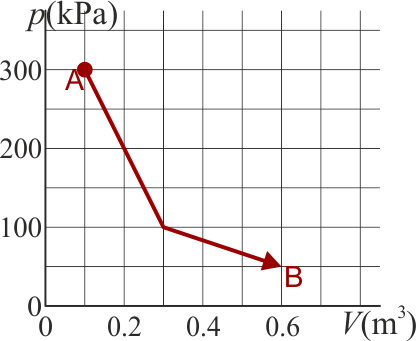
- ¿Cuánto es la variación de la energía interna del gas?
- ¿Cuánto calor entra en el gas en este proceso?
Variación de la energía interna
La variación en la energía interna es
Si sustituimos la relación entre la capacidad calorífica molar y la constante de los gases ideales queda
El valor numérico de esta cantidad es
El estado final tiene la misma temperatura que el inicial y no hay variación en la energía interna.
Calor
Calculamos el calor aplicando el primer principio de la termodinámica
A su vez, el trabajo lo calculamos a partir de la integral de la presión
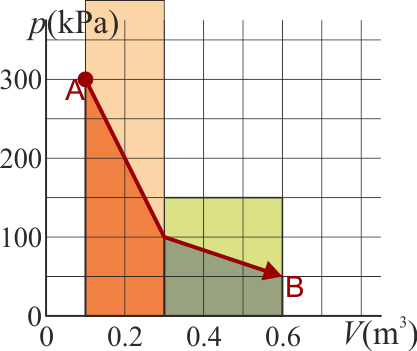
El área bajo la curva es la suma de dos trapecios. Su valor puede hallarse o bien aplicando la fórmula del área de un trapecio u observando que cada uno es la mitad de un rectángulo. Por ello





