Varilla apoyada en una esquina (CMR)

Enunciado

Dos masas iguales m están unidas por una varilla rígida ideal de longitud b. La varilla está apoyada en el suelo y en una pared vertical, formando la varilla un ángulo θ con la vertical. Todo el sistema está contenido en el plano vertical OXY

1. Suponga que el sistema está en equilibrio. Calcule el mínimo valor que debe tener el coeficiente de rozamiento μ entre la varilla y el suelo para que esto ocurra. Para esta situación, ¿cuánto valen las reacciones normales del suelo y la pared, la fuerza de rozamiento y la tensión de la varilla?
2. Suponga que no existe rozamiento y que la varilla va cayendo apoyada en el suelo y la pared. Para el momento en que la varilla forma un ángulo θ con la vertical y este ángulo varía con una velocidad ${\dot {\theta }}$, ¿cuánto valen las reacciones y la tensión?
3. Determine la ecuación de movimiento para la varilla.
4. Si inicialmente la varilla se encuentra en reposo en posición vertical y a partir de ahí comienza a deslizar, ¿para qué ángulo se separa de la pared?

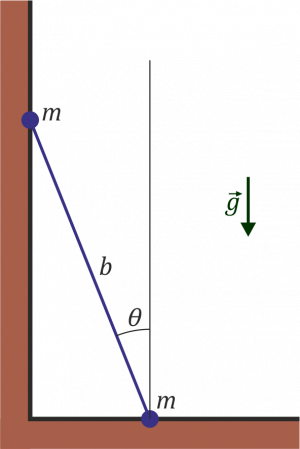
Estado de equilibrio

Si las masas permanecen reposo, la suma de fuerzas sobre cada una de ellas dee ser nula. Sobre la partícula A, situada en el suelo, actúan su peso, la rección normal del suelo, la fuerza de rozamiento, horizontal, y la tensión de la varilla. La condición de equilibrio es

${\vec {0}}=-mg{\vec {\jmath }}+F_{Ay}{\vec {\jmath }}+F_{Ax}{\vec {\imath }}+F_{T}(S{\vec {\imath }}-C{\vec {\jmath }})$

con $C=\cos(\theta )$, $S=\mathrm {sen} (\theta )$. Obsérvese que hemos supuesto que la tensión va hacia afuera de la varilla, esto es, que se halla en compresión. No hay problema en suponer que va hacia adentro, pero en ese caso nos resultará un valor negativo. La reacción normal y la fuerza de rozamiento están escritas como dos componentes de una fuerza de reacción en A. Aunque el rozamiento va a ir para atrás, se ha optado por indicar simplemente que va en la dirección horizontal, dejando que sean las ecuaciones las que determinen el signo (hay veces que el rozamiento va en sentido opuesto al que se supone).

Separando por componentes

$\left\{{\begin{array}{rcrcl}x:&\quad &0&=&F_{Ax}+F_{T}S\\y:&\quad &0&=&-mg+F_{Ay}-F_{T}C\end{array}}\right.$

Para la masa B, actúan su peso, la reacción normal de la pared y la tensión. No hay rozamiento

${\vec {0}}=-mg{\vec {\jmath }}+F_{Bx}{\vec {\imath }}-F_{T}(S{\vec {\imath }}-C{\vec {\jmath }})$

Separando por componentes

$\left\{{\begin{array}{rcrcl}x:&\quad &0&=&F_{Bx}-F_{T}S\\y:&\quad &0&=&-mg+F_{T}C\end{array}}\right.$

De aquí obtenemos la tensión

$F_{T}={\frac {mg}{C}}$

La reacción en B

$F_{Bx}=F_{T}S={\frac {mgS}{C}}$

La fuerza normal en A

$F_{Ay}=mg+F_{T}C=2mg\,$

y la fuerza de rozamiento

$F_{Ax}=-F_{T}S=-{\frac {mgS}{C}}$

El valor mínimo del coeficiente de rozamiento lo obtenemos de la condición

$|{\vec {F}}_{r}|\leq \mu |{\vec {F}}_{n}|$

que en este caso nos da

$|F_{Ax}|\leq |F_{Ay}|\qquad \Rightarrow \quad {\frac {mgS}{C}}\leq \mu (2mg)\qquad \Rightarrow \qquad \mu \geq {\frac {\tan {}(\theta )}{2}}$

Estado de movimiento

Si no hay rozamiento, la barra desliza apoyada en la pared y en el suelo. La masa A se mueve horizontalmente con posición, velocidad y aceleración

${\overrightarrow {OA}}=bS{\vec {\imath }}\qquad \qquad {\vec {v}}_{A}=b{\dot {\theta }}C{\vec {\imath }}\qquad {\vec {a}}_{A}=b\left({\ddot {\theta }}C-{\dot {\theta }}^{2}S\right){\vec {\imath }}$

y las de la masa B son

${\overrightarrow {OB}}=bC{\vec {\jmath }}\qquad \qquad {\vec {v}}_{B}=-b{\dot {\theta }}S{\vec {\imath }}\qquad {\vec {a}}_{B}=-b\left({\ddot {\theta }}S+{\dot {\theta }}^{2}C\right){\vec {\jmath }}$

Por ello, las ecuaciones de movimiento para la masa A y B quedan

$\left\{{\begin{array}{rcrcl}x_{A}:&\quad &m(b{\ddot {\theta }}C-b{\dot {\theta }}^{2}S)&=&F_{T}S\\y_{A}:&\quad &0&=&-mg+F_{Ay}-F_{T}C\\x_{B}:&\quad &0&=&F_{Bx}-F_{T}S\\y_{B}:&\quad &-mb({\ddot {\theta }}S+{\dot {\theta }}^{2}C)&=&-mg+F_{T}C\end{array}}\right.$

Las ecuaciones en las que aparecen $F_{Ay}$ y $F_{Bx}$, que son cantidades desconocidas, nos permiten halar estas fuerzas de reacción una vez que tengamos la ecuación de movimiento.

Para elimnar la tensión, que también es una fuerza de valor desconocido, multiplicamos la primera ecuación por el coseno, la 4ª por el seno y restamos. Queda

$mb{\ddot {\theta }}=mgS\qquad \Rightarrow \qquad {\ddot {\theta }}={\frac {g}{b}}\mathrm {sen} (\theta )$

Esta es la ecuación de movimiento para la barra. Se comporta como un péndulo invertido, que tiene una posición de equilibrio vertical, pero es inestable y cualquier perturbación la hace descender.

Una vez que tenemos esta ecuación, podemos hallar las fuerzas de reacción.

Si multiplicamos la primera ecuación por el seno y la cuarta por el coseno y sumamos queda

$F_{T}=-mb{\dot {\theta }}^{2}+mgC$

Vemos que en este caso la varilla no está siempre en compresión. Si se mueve muy rápido pasa a estar en tracción.

La reacción en el suelo vale

$F_{Ay}=mg+F_{T}C=mg(1+C^{2})-mb{\dot {\theta }}^{2}C$

y en la pared

$F_{Bx}=F_{T}S=-mb{\dot {\theta }}^{2}S+mgCS$

Separación de la pared

En este sistema se conserva la energía mecánica, ya que no hay rozamiento y las fuerzas de reacción son perpendiculares a los desplazamientos. La tensióntampoco desarrolla potencia ya que lo que empuja a la masa A se compensa con lo que tira de la B.

La energía cinética vale

$T={\frac {1}{2}}m|{\vec {v}}_{A}|^{2}+{\frac {1}{2}}m|{\vec {v}}_{B}|^{2}={\frac {1}{2}}mb^{2}{\dot {\theta }}^{2}$

y la potencial

$U=m\cdot 0+mgbC=mgbC\,$

Por tanto, se cumple

${\frac {1}{2}}mgb^{2}{\dot {\theta }}^{2}+mgbC=E=\mathrm {cte.}$

Esto nos permite despejar la velocidad angular en función del ángulo

${\dot {\theta }}^{2}={\frac {2E}{mb^{2}}}-{\frac {2gC}{mb}}$

Si llevamos este resultado a la expresión de la fuerza de reacción de la pared queda

$F_{Bx}=-mb\left({\frac {2E}{mb^{2}}}-{\frac {2gC}{mb}}\right)+mgCS=-{\frac {2E}{b}}+3mgC$

Vemos que dependiendo de la energía, esta fuerza puede llegar a anularse o, aparentemente, a hacerse negativa. Pero esto último es imposible ya que el vínculo es unilateral. La pared no puede tirar de la masa hacia ella. Por tanto, en el momento en que la fuerza de reacción se anula, lo que ocurre es que la varilla se separa de la pared y pasa a estar apoyada solo en el suelo.

Esto ocurre para el ángulo que cumple

$-{\frac {2E}{b}}+3mgC=0\qquad \Rightarrow \qquad \cos(\theta )={\frac {2E}{3mgb}}$

Si la varilla parte desde el reposo en la posición vertical su energía mecánica vale

$E=0+mgb=mgb\,$

Por lo cual el ángulo de separación cumple

$\cos(\theta )={\frac {2}{3}}\qquad \Rightarrow \qquad 0.841\,\mathrm {rad} =48.2^{\circ }$

Situación tras la separación

Una vez que se separa el movimiento pasa a tener dos grados de libertad y hay que analizar qué le ocurre a la posición horizontal y al ángulo de inclinación.

Si llamamos x a la distancia del extrem B a la pared, la aceleración de B es ahora

${\vec {a}}_{B}={\ddot {x}}{\vec {\imath }}-\left(b{\ddot {\theta }}S+b{\dot {\theta }}^{2}C\right){\vec {\jmath }}$

y la de A

${\vec {a}}_{A}=\left({\ddot {x}}+b{\ddot {\theta }}C-b{\dot {\theta }}^{2}S\right){\vec {\imath }}$

Las ecuaciones de movimiento son ahora

$\left\{{\begin{array}{rcrcl}x_{A}:&\quad &m\left({\ddot {x}}+b{\ddot {\theta }}C-b{\dot {\theta }}^{2}S\right)&=&F_{T}S\\y_{A}:&\quad &0&=&-mg+F_{Ay}-F_{T}C\\x_{B}:&\quad &{\ddot {x}}&=&-F_{T}S\\y_{B}:&\quad &-mb\left({\ddot {\theta }}S+{\dot {\theta }}^{2}C\right)&=&-mg+F_{T}C\end{array}}\right.$

Sumamos la primera y la tercera y queda

$2{\ddot {x}}+b{\ddot {\theta }}C-b{\dot {\theta }}^{2}S=0\,$

y de la primera y la cuarta

${\ddot {x}}C+b{\ddot {\theta }}=gS\,$

Las condiciones iniciales para este sistema las dan la posición y la velocidad en el instante de la separación

$x=0\qquad \qquad \theta =\arccos \left({\frac {2}{3}}\right)\qquad \qquad {\dot {x}}=0\qquad \qquad {\dot {\theta }}={\sqrt {\frac {2gb}{3}}}$

La última condición sale de la ley de conservación de la energía.