Unidad imaginaria
Se define la raíz cuadrada de -1 como la unidad imaginaria

En matemáticas se suele representar como i. En ingeniería como j para evitar confusiones con la intensidad de corriente.
Con ayuda de la unidad imaginaria se puede calcular la raíz de cualquier número negativo

Números complejos
Se definen a partir de un par de números reales como

Los números complejos tienen numerosas similitudes con los pares de 
 pero con propiedades adicionales.
pero con propiedades adicionales.
Parte real y parte imaginaria
Para un número complejo de la forma anterior
- Parte real
- Es el sumando que no multiplica a la unidad imaginaria

- Parte imaginaria
- Es el coeficiente que multiplica a la unidad imaginaria.

Representación en el plano complejo
Un número complejo puede representarse como un punto  en un plano (denominado plano complejo). La parte real es la abcisa y la imaginaria la ordenada. El eje real es el conjunto de todos los complejos puramente reales y el eje imaginario el de todos los imaginarios puros.
en un plano (denominado plano complejo). La parte real es la abcisa y la imaginaria la ordenada. El eje real es el conjunto de todos los complejos puramente reales y el eje imaginario el de todos los imaginarios puros.

Alternativamente, en lugar de un punto puede usarse un vector (llamado afijo) que une el origen  con el punto P(x,y) del plano.
con el punto P(x,y) del plano.
Forma polar de un número complejo
Alternativamente, un número complejo puede representarse por su módulo (el del afijo)

y su argumento, que es el ángulo que el afijo forma con el eje real

Las relaciones inversas de estas son

y por tanto

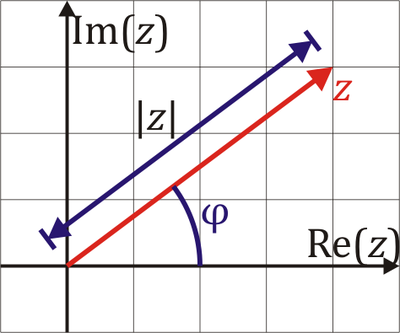
Existen distintas formas de expresar un número complejo en forma polar, una de ellas es

así

Conjugado de un número complejo
A partir de un número complejo  se define su conjugado
se define su conjugado

es decir, con la misma parte real y con la parte imaginaria cambiada de signo.
Gráficamente el punto  es el simétrico de
es el simétrico de  respecto al eje real.
respecto al eje real.
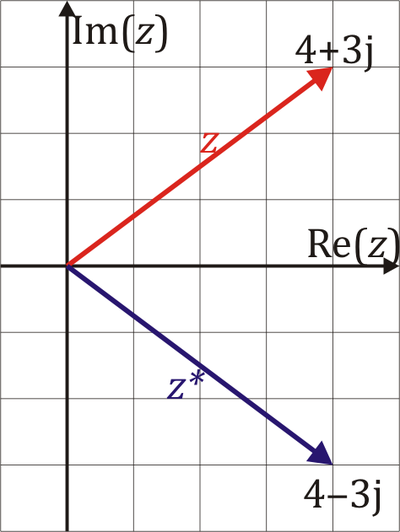
En la forma polar, el conjugado tiene el mismo módulo y argumento opuesto

Cálculo de la parte real y parte imaginaria
Si conocemos un complejo y su conjugado, la parte real y la imaginaria pueden calcularse como

Cálculo del módulo
A partir del complejo y su conjugado

Igualdad de complejos
Dos complejos son iguales cuando son iguales sus partes reales y sus partes imaginarias

En términos de módulo y argumento, son iguales cuando tienen el mismo módulo y su argumento se diferencia en un número entero de vueltas

Suma de números complejos
Para sumar dos complejos se suman sus partes reales y sus partes imaginarias

La suma de complejos verifica las propiedades que definenen un grupo abeliano (asociativa, elemento neutro, elemento simétrico y conmutativa).

Gráficamente, la suma de números complejos equivale a la suma de vectores en el plano, empleando la regla del paralelogramo o del triángulo.
Producto de números complejos
Aplicando la fórmula del producto de dos binomios

lo que da

En forma polar, se cumple que los módulos se multiplican y los argumentos se suman

Gráficamente, el producto de un número complejo  por otro
por otro  es una combinación de dos pasos:
es una combinación de dos pasos:
- Un giro de un ángulo

- Una dilatación por un factor

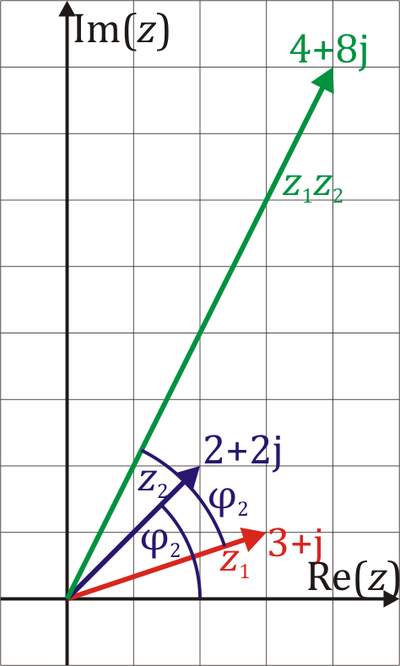
En particular, si  es unitario (módulo unidad), la multiplicación por él se reduce a un giro, mientras que si es no unitario pero puramente real el producto se reduce a una dilatación.
es unitario (módulo unidad), la multiplicación por él se reduce a un giro, mientras que si es no unitario pero puramente real el producto se reduce a una dilatación.
Puesto que un complejo y su conjugado tienen argumentos opuestos

División de números complejos
Para dividir dos números complejos se usa la propiedad

de forma que el cociente entre dos complejos se reduce a un producto

Así, por ejemplo

Empleando la forma polar equivale a dividir los módulos y restar los argumentos,

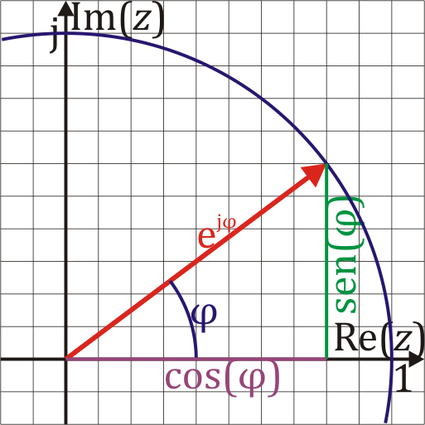
Fórmula de Euler
Empleando el desarrollo en serie de potencias de la exponencial, el seno y el coseno; o bien a partir de la ecuación del oscilador armónico se llega a que, para todo número real 

es decir, la exponencial de un número imaginario puro  es un complejo unitario cuya parte real es el coseno del ángulo
es un complejo unitario cuya parte real es el coseno del ángulo  y su parte imaginaria es el seno del mismo ángulo, es decir, que se trata del complejo unitario que forma un ángulo
y su parte imaginaria es el seno del mismo ángulo, es decir, que se trata del complejo unitario que forma un ángulo  con el eje real
con el eje real
Como caso particulares tenemos

La última de ellas se escribe habitualmente

La exponencial de un número imaginario se relaciona directamente con la forma polar de un número complejo

De aquí es inmediata la fórmula para el producto de dos complejos

y lo mismo para el cociente.
Al ser unitaria la exponencial de un número imaginario resulta que la multiplicación de un complejo por  equivale a una rotación de su afijo un ángulo
equivale a una rotación de su afijo un ángulo 
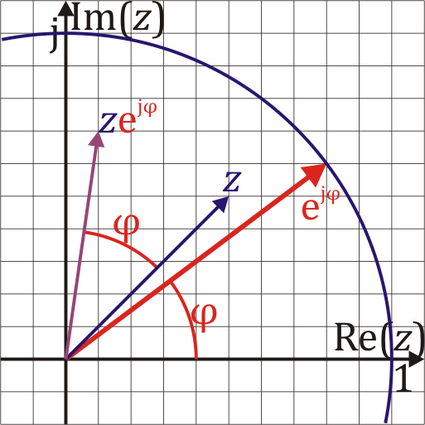
En particular:
- Multiplicar por la unidad imaginaria j equivale a girar un ángulo de 90º
- Multiplicar por -1 equivale a girar un ángulo de 180º

Exponencial de un número complejo
Empleando la fórmula de Euler

es decir

Logaritmo de un número complejo
Invirtiendo la relación anterior queda

o

El logaritmo de un número complejo es una función multivaluada ya que para un número complejo hay infinitos argumentos posibles, que se diferencian en un número entero de vueltas en el plano complejo alrededor del origen.
Potencias complejas
Empleando la exponencial y el logaritmo puede hallarse cualquier potencia compleja

Así, por ejemplo,

Como caso particular importante, la raíz cuadrada de un número complejo es otro complejo que cumple

Funciones trigonométricas
Partimos de la fórmula de Euler

que, conjugada, da

Despejando entre estas dos queda una fórmula alternativa para el coseno

y otra para el seno

Estas relaciones pueden generalizarse a cualquier complejo, no solo a valores reales.
Funciones hiperbólicas
Análogamente a las funciones trigonométricas, se definen el coseno hiperbólico

y el seno hiperbólico


































































