Tabla de fórmulas de trigonometría
Secciones
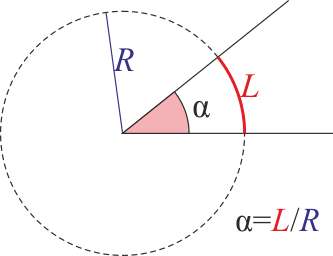
Ángulos
Definición
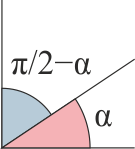
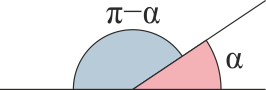
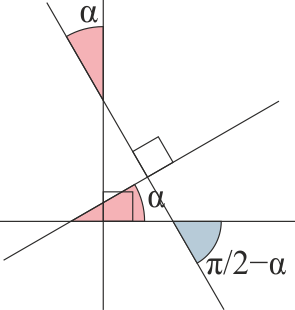
Complementario y suplementario
- Complementario
- Suplementario
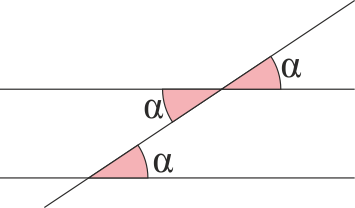
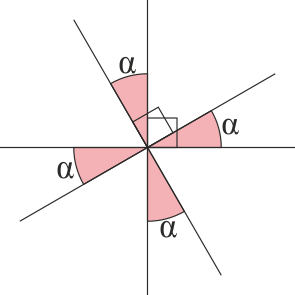
Opuestos por el vértice y alternos
Rotación de ejes
- Mismo origen
- Diferente origen
Definiciones
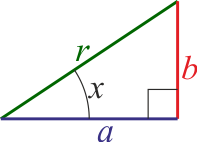
Geométrica
- Coseno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x)=\frac{a}{r}}
- Seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x) = \frac{b}{r}}
Analítica
El argumento Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} debe estar expresado en radianes
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x) = 1 -\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x) = x -\frac{x^3}{6}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots}
Exponenciales complejas
- (Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{j}=\sqrt{-1}} )
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x) = \frac{\mathrm{e}^{\mathrm{j}x}+\mathrm{e}^{-\mathrm{j}x}}{2}}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x) = \frac{\mathrm{e}^{\mathrm{j}x}-\mathrm{e}^{-\mathrm{j}x}}{2\mathrm{j}}}
Funciones adicionales
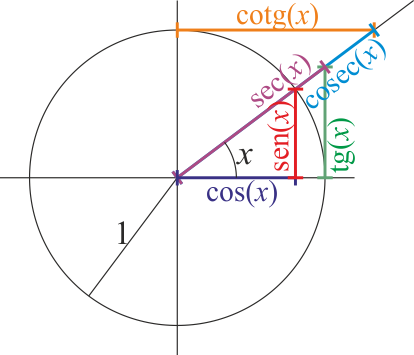
- Tangente
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(x) = \frac{\mathrm{sen}(x)}{\cos(x)} = \frac{b}{a}}
- Cotangente
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{cotg}(x) = \frac{\cos(x)}{\mathrm{sen}(x)} = \frac{1}{\mathrm{tg}(x)}=\frac{a}{b}}
- Secante
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sec}(x) = \frac{1}{\cos(x)}=\frac{r}{a}}
- Cosecante
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{cosec}(x) = \frac{1}{\mathrm{sen}(x)}=\frac{r}{b}}
En la circunferencia unidad
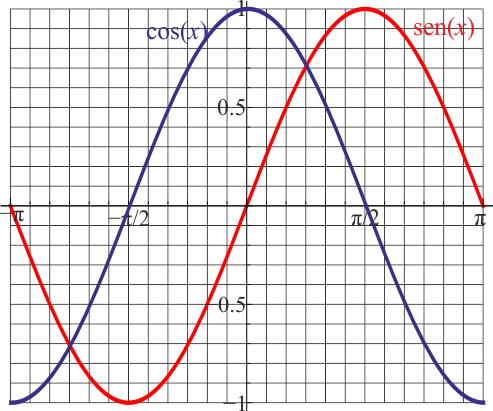
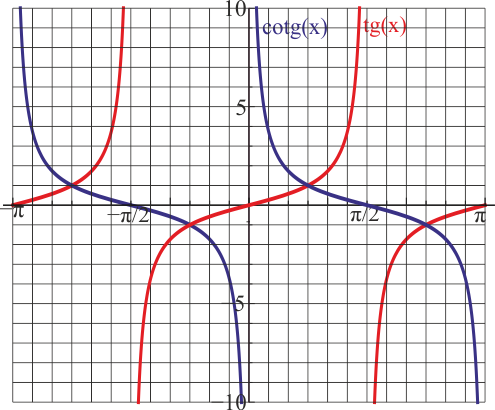
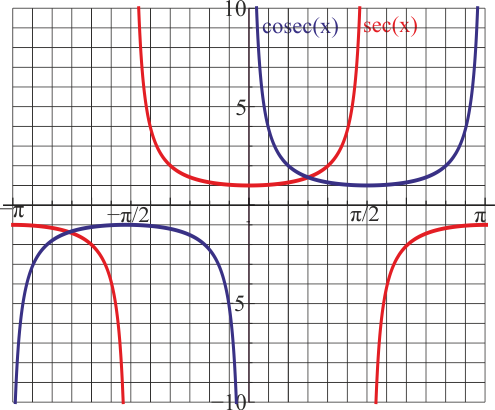
Gráficas desde −π a π
- Seno y coseno
- Tangente y cotangente
- Secante y cosecante
Relaciones entre funciones
Identidades básicas
En función de la tangente
En función de la tangente del ángulo mitad
Tabla de valores particulares
| ° | rad | sen | cos | tg |
|---|---|---|---|---|
| Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \pi/2\,} | Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \sqrt{4}/2=1} | Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0\,} | Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \infty} |
Relaciones entre cuadrantes
- Ángulo complementario
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(\frac{\pi}{2}-x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}-x\right)=\mathrm{sen}(x)}
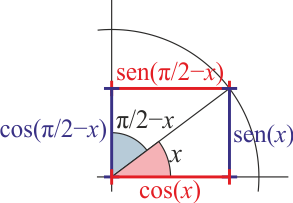
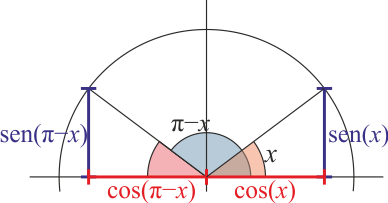
- Ángulo suplementario
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(\pi-x\right)=\mathrm{sen}(x)\qquad \cos\left(\pi-x\right)=-\cos(x)}
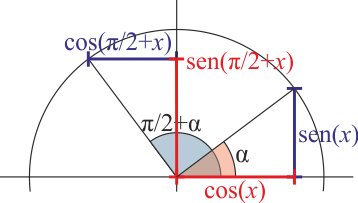
- Giro de un cuadrante
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(\frac{\pi}{2}+x\right)=\cos(x)\qquad \cos\left(\frac{\pi}{2}+x\right)=-\mathrm{sen}(x)}
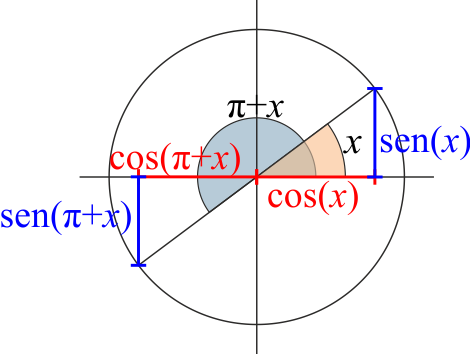
- Giro de dos cuadrantes
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(\pi+x\right)=-\mathrm{sen}(x)\qquad \cos\left(\pi+x\right)=-\cos(x)}
- Cambio de signo
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(-x\right)=-\mathrm{sen}(x)\qquad \cos\left(-x\right)=\cos(x)}
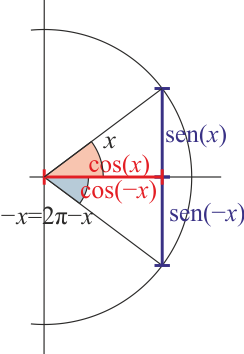
Suma y diferencia de ángulos
- Seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x+y)=\mathrm{sen}(x)\cos(y)+\cos(x)\mathrm{sen}(y)\,}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x-y)=\mathrm{sen}(x)\cos(y)-\cos(x)\mathrm{sen}(y)\,}
- Coseno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x+y)=\cos(x)\cos(y)-\mathrm{sen}(x)\mathrm{sen}(y)\,}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x-y)=\cos(x)\cos(y)+\mathrm{sen}(x)\mathrm{sen}(y)\,}
- Tangente
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(x+y)=\frac{\mathrm{tg}(x)+\mathrm{tg}(y)}{1-\mathrm{tg}(x)\mathrm{tg}(y)}}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(x-y)=\frac{\mathrm{tg}(x)-\mathrm{tg}(y)}{1+\mathrm{tg}(x)\mathrm{tg}(y)}}
Ángulo doble y ángulo mitad
Ángulo doble
- Seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(2x)=2\,\mathrm{sen}(x)\cos(x)\,}
- Coseno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(2x)=\cos^2(x)-\mathrm{sen}^2(x)\,}
- Tangente
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}(2x)=\frac{2\,\mathrm{tg}(x)}{1-\mathrm{tg}^2(x)}}
Ángulo mitad
- Seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{2}}}
- Coseno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos\left(\frac{x}{2}\right)=\sqrt{\frac{1+\cos(x)}{2}}}
- Tangente
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{tg}\left(\frac{x}{2}\right)=\sqrt{\frac{1-\cos(x)}{1+\cos(x)}}=\frac{\mathrm{sen}(x)}{1+\cos(x)}}
Sumas en productos
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x)+\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{sen}(x)-\mathrm{sen}(y) = 2\,\mathrm{sen}\left(\frac{x-y}{2}\right)\cos\left(\frac{x+y}{2}\right)}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x)+\cos(y) = 2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \cos(x)-\cos(y) = -2\,\mathrm{sen}\left(\frac{x+y}{2}\right)\mathrm{sen}\left(\frac{x-y}{2}\right)}
Derivadas y primitivas
El argumento debe estar obligatoriamente en radianes
Derivadas
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{sen}(x)) = \cos(x)}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\ }{\mathrm{d}x}(\cos(x)) = -\,\mathrm{sen}(x)}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathrm{d}\ }{\mathrm{d}x}(\mathrm{tg}(x)) = \frac{1}{\cos^2(x)}=1+\mathrm{tg}^2(x)}
Primitivas
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \int \mathrm{sen}(x)\mathrm{d}x = -\cos(x)+C}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \int \cos(x)\mathrm{d}x = \mathrm{sen}(x)+C}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \int \mathrm{tg}(x)\mathrm{d}x = -\ln(\cos(x))+C}
Fórmula de Euler
- Fórmula general
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{e}^{\mathrm{j}x}=\cos(x)+\mathrm{j}\,\mathrm{sen}(x)\qquad (\mathrm{j}=\sqrt{-1})}
- Casos particulares
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{e}^{\mathrm{j}\pi/2} = \mathrm{j}\,}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{e}^{\mathrm{j}\pi} = -1\,}
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathrm{e}^{2\pi\mathrm{j}} = 1\,}
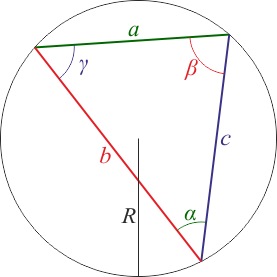
Teoremas del seno y del coseno
Teorema del seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{a}{\mathrm{sen}(\alpha)}=\frac{b}{\mathrm{sen}(\beta)}=\frac{c}{\mathrm{sen}(\gamma)}=2R}
(Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} : radio de la circunferencia circunscrita)
Teorema del coseno
Misma notación que en el teorema del seno
- Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a^2 = b^2 + c^2-2bc\cos(\alpha)\,}
y las correspondientes a los otros dos ángulos.
Resolución de triángulos
Misma notación que en el teorema del seno y del coseno.
Se trata de dados tres datos (lados o ángulos) hallar los tres restantes.
Dados los tres lados
Por el teorema del coseno se determinan los tres ángulos. Para Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha}
y análogamente para los otros dos.
Dados dos lados y el ángulo que abarcan
Si conocemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b} y el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \gamma} por el teorema del coseno hallamos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle c}
una vez conocidos los tres lados podemos aplicar el caso anterior o bien emplear el teorema del seno
Dados dos lados y otro ángulo
Si conocemos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle b} y el ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \beta} por el teorema del seno hallamos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha}
y aplicando que los ángulos suman Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \pi}
y a partir de ahí se sigue como en los casos anteriores.
Dado un lado y dos ángulos
Si concemos el lado Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a} y los ángulos Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \beta} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \gamma} , hallamos en primer lugar Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha}
y luego aplicamos el teorema del seno
Dados los tres ángulos
En ese caso no se pueden dar los tres lados, ya que todos los triángulos semejantes tienen los mismos ángulos independientemente de su tamaño. No obstante, puede darse a proporción entre sus lados mediante el teorema del seno.