Segunda Convocatoria Ordinaria 2023/24 (MR G.I.C.)
Aro articulado en el extremo de una barra
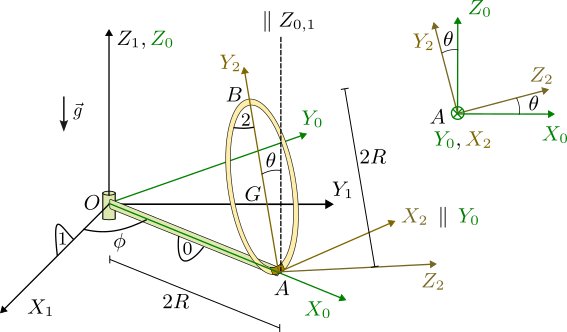
Una barra (sólido "0") homogénea y delgada de longitud y masa despreciable está articulada en el punto fijo . La barra está siempre contenida en el plano y rota alrededor del eje fijo . El sistema de ejes se elige de modo que el eje contenga siempre a la barra. Un aro (sólido "2") de radio y masa , se articula sobre el extremo de la barra "0", de modo que puede rotar alrededor del eje , paralelo en todo momento al eje . El sistema de ejes "2" se elige de modo que sea perpendicular al plano del aro y el eje sea paralelo al . De este modo, el eje contiene siempre al centro del aro y el plano coincide con el plano El aro no rota alrededor del eje . El sistema está sometido a la acción de la gravedad, como se indica en la figura.
Nota: Utiliza la base vectorial asociada al sólido "0" para hacer todos los cálculos.
- Expresa los vectores de la base del sistema "2" en función de los vectores de la base "0", y los de la base "0" en función de los de la base "2".
- Encuentra la reducción cinemática de los movimientos {01}, {20} y {21} en el punto .
- Calcula la cantidad de movimiento del aro y el o angular del aro en su centro de masas.
- Dibuja el diagrama de fuerzas y momentos sobre la barra y el aro.
- Escribe la expresión genérica de las fuerzas y momentos activos y vinculares que actúan sobre cada sólido. ¿Cuántas incógnitas tiene el problema?
- Escribe la expresión vectorial del T.C.M. y el T.M.C. aplicados a los dos sólidos ¿Cuántas ecuaciones pueden obtenerse? (No hay que escribir las ecuaciones)
- Escribe la energía potencial total del sistema "0" + "2".
- ¿Qué integral o integrales primeras del sistema "0" + "2" existen? ¿Por qué? (No hay que escribir las expresiones).
Supondremos a partir de ahora que la función de Lagrange tiene la forma siendo , y constantes conocidas.
- Aplica el método de los multiplicadores de Lagrange para encontrar las ecuaciones que describen el movimiento de los sólidos si se verifican estas dos ligaduras:
- En tenemos , y . Se aplica una percusión en el punto del aro. Determina el valor de y . (Las ligaduras del apartado anterior no se aplican en este apartado)


























