Placa cuadrada pivotando con muelle
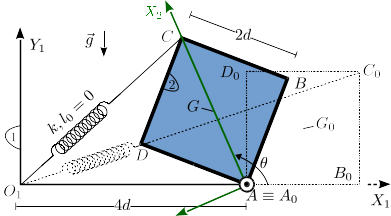
El sólido "2' es una placa cuadrada y homogénea, de lado y masa . La placa está articulada en su vértice , que permanece fijo. El vértice de la placa está conectado a un muelle de constante elástica y longitud natural nula, anclado en el punto . En el instante inicial la posición de la placa está indicada en la figura por el cuadrado punteado. En esa posición inicial, el lado no está apoyado en ninguna superficie. La gravedad actúa en la dirección vertical hacia abajo. Durante el movimiento de la placa el muelle permanece siempre estirado.
- ¿Qué valor debe tener para que la posición inicial sea una posición de equilibrio? Encuentra la reducción vincular en para la situación de equilibrio.
- Determina la reducción cinemática del movimiento {21} en el punto de la placa, así como su derivada temporal.
- Una pequeña perturbación hace que la placa empiece a girar con velocidad angular inicial . Encuentra la expresión de la energía cinética de la placa durante su movimiento (ver Nota).
- Encuentra una integral primera del movimiento. Supón que el valor de corresponde a la condición de equilibrio del apartado 1.
- Considerando el valor de del apartado anterior, discute razonadamente la estabilidad del equilibrio del apartado 1.
Nota: El momento de inercia de una placa homogénea cuadrada de masa y lado , respecto a un eje perpendicular a ella que pasa por su centro es .
Barra con centro deslizando sobre eje
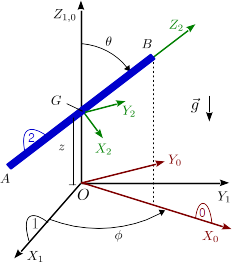
Una barra homogénea delgada (sólido "2") de masa y longitud se mueve de modo que su centro se encuentra siempre sobre el eje . La barra tiene dos grados de libertad de rotación. El sistema auxiliar se define de modo que la barra esté siempre contenida en el plano . La barra está sometida a la acción de la gravedad, como se indica en la figura. El contacto de la barra con el eje es liso.
- Calcula las reducciones cinematicas en el centro de la barra de los tres movimientos que se pueden definir en el problema.
- Encuentra la expresión del momento cinético de la barra respecto de su centro.
- Encuentra la expresión de la energía cinética de la barra.
- Escribe la Lagrangiana del sistema, así como una integral primera que no sea la energía mecánica.
- En el instante inicial, el centro de la barra se encuentra en el punto y los valores iniciales de las coordenadas angulares son y . La barra se encuentra en reposo. Se ejerce una percusión aplicada en el punto . Determina los valores de las velocidades generalizadas justo después de la percusión.



















