Segunda Convocatoria Ordinaria 2012/13 (G.I.C.)

Partícula sobre una circunferencia tirada por una cuerda

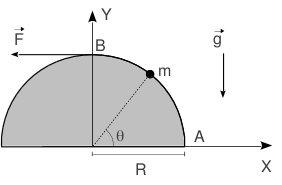
Una partícula de masa $m$ se mueve a lo largo de una circunferencia de radio $R$ sin rozamiento. Una fuerza horizontal tira de ella por medio de una cuerda que se mantiene siempre pegada a la circunferencia. La partícula está sometida a la acción de la gravedad. }

1. Expresa los vectores de posición, velocidad y aceleración de la partícula en coordenadas polares.
2. Dibuja el diagrama de cuerpo libre de la partícula y expresa las fuerzas que actúan sobre ella en coordenadas polares.
3. Escribe las ecuaciones de movimiento de la partícula. ¿Cuál es la condición que debe cumplir la fuerza ${\vec {F}}$ para que la celeridad de la partícula sea constante durante el movimiento? ¿Cuanto vale la fuerza de reacción vincular en este caso?
4. Supongamos que la partícula parte del reposo desde el punto $A$. Al llegar al punto $B$ su velocidad es de 12.0 m/s. Calcula el trabajo realizado por la fuerza $F$ en el movimiento desde $A$ hasta $B$.

Datos numéricos: $m=1.00\,\mathrm {kg}$, $R=2.00\,\mathrm {m}$, $g=9.81\,\mathrm {m/s}$.

Barra apoyada sobre un triángulo

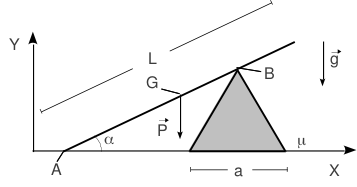
Una barra de longitud $L$ se apoya en el suelo y en el vértice de un triángulo equilátero de lado $a$. El ángulo que forma la barra con el suelo es $\alpha$. El peso de la barra es $P$, y se aplica en su punto medio $G$. El peso del triángulo es despreciable. El contacto con el suelo es rugoso para la barra y el triángulo, con un coeficiente de rozamiento $\mu$. El contacto entre la barra y el triángulo en el punto $B$ es liso.

1. Dibuja el diagrama de cuerpo libre de la barra y el triángulo.
2. Calcula todas las fuerzas del apartado anterior en condiciones de equilibrio estático.
3. ¿Que condición debe cumplir $\alpha$ para que el triángulo no vuelque en ningun caso?
4. Analiza las condiciones que debe cumplir $\mu$ para que se mantenga el equilibrio frente a deslizamiento.