Problemas de energía y leyes de conservación (GIOI)
Secciones
Impacto de bala en gelatina
El rozamiento que experimenta una pequeña partícula en un medio denso y viscoso como un aceite es de la forma \vec{F}_r=-γv. Se construye un sensor de balística, en el que una bala de masa m impacta horizontalmente en un bloque de gelatina en el que se cumple la ley anterior. Se sabe que la bala recorre una distancia b hasta pararse. Demuestre que la cantidad mv+γx es una constante de movimiento y a partir de ella determine la velocidad inicial de la bala. Solución
Conservación en un movimiento rectilíneo y uniforme
Una partícula de masa describe el movimiento rectilíneo y uniforme
Demuestre que su cantidad de movimiento, su momento cinético respecto al origen de coordenadas y su energía cinética permanecen constantes. Halle el valor de estas tres cantidades.
Leyes de conservación en polares y cilíndricas
Una partícula de masa describe el movimiento expresado en cilíndricas
Determine si se conserva la cantidad de movimiento, el momento cinético respecto al origen de coordenadas y la energía cinética. En su caso, halle el valor de las constantes.
Ecuación del péndulo empleando el momento cinético
Empleando el teorema del momento cinético, determine la ecuación del movimiento del péndulo simple. Solución
Momento cinético en movimiento parabólico
Una partícula se mueve con velocidad horizontal constante , hasta que llega a un barranco vertical, a partir del cual cae por acción de la gravedad. Durante el movimiento de caída…
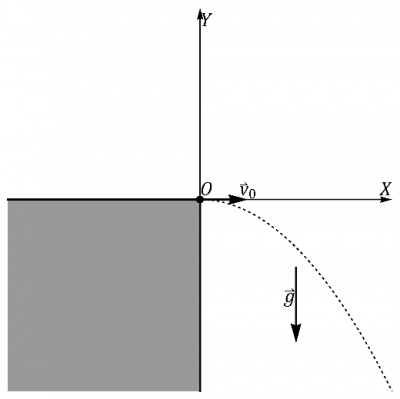
- ¿Cuánto vale el momento cinético de la partícula respecto al origen de coordenadas, O?
- ¿Cuánto vale respecto a O el momento de las fuerzas que actúan sobre la partícula?
Trabajo realizado por la gravedad
Calcule el trabajo realizado por la gravedad cuando una partícula de masa m que pasa de estar a una altura 2R a estar al nivel del suelo
- si el movimiento es una recta vertical
- Desciende a lo largo de una semicircunferencia de radio R.
Trabajo realizado por el rozamiento
Calcule el trabajo realizado por la fuerza de rozamiento seco sobre una masa m que se hace deslizar por una mesa horizontal con la cual tiene un coeficiente de rozamiento μ, si
- el movimiento es a largo de un segmento de longitud 2R,
- el deslizamiento es a largo de una semicircunferencia de radio R.
Conservación en un oscilador armónico tridimensional
Una partícula de masa se encuentra sometida exclusivamente a una fuerza que satisface la ley de Hooke
siendo su posición y velocidad iniciales
- Calcule el momento cinético de la partícula respecto al origen de coordenadas
- Halle la energía mecánica de la partícula
- Determine las distancias máxima y mínima a las que pasa del origen, así como la rapidez mínima que alcanza
Rapidez y tensión de un péndulo
Empleando la ley de conservación de la energía, determine la velocidad con la que un péndulo simple de masa y longitud pasa por su punto más bajo, como función del ángulo máximo con el que se separa de la vertical.
Compare este resultado con el que se obtiene empleando la aproximación lineal. Determine el error relativo cometido con esta aproximación para , ,…
Determine la tensión de la cuerda en el punto más bajo y en el punto de máxima separación de la vertical. en función del ángulo
Trace la curva de energía potencial en función del ángulo θ con el que se separa de la vertical. Suponga que el punto más bajo corresponda a U = 0. A la vista de la curva,
- ¿Qué puntos de equilibrio existen? ¿Son estables o inestables?
- ¿Cómo es el movimiento si la energía mecánica vale mgb? ¿Y si vale 3mgb?
Percusión en un péndulo
Un péndulo simple está formado por una masa m suspendida verticalmente en el extremo P de una varilla rígida de longitud , articulada en su otro extremo a un punto fijo O. Estando la masa en reposo en el punto más bajo, se le comunica una energía cinética K mediante un golpe seco.
- ¿Cuánto vale, en módulo, el impulso que recibe la partícula?
- ¿Cuánto vale el ángulo máximo que se desvía la varilla de la vertical?
- ¿Cuánto vale la tensión de la varilla justo después de que se golpee la masa?
Anilla ensartada en un aro
Se tiene un aro circular de radio situado verticalmente. Determine la velocidad que debe comunicarse a una partícula de masa situada en el punto más bajo del aro para que sea capaz de llegar hasta el punto más alto si la partícula es:
- Una anilla ensartada en el aro
- Una bolita que desliza por el interior del aro, sin estar unida a él.
Calcule la reacción que ejerce el aro sobre la partícula en el punto más bajo y en el más alto, para los dos casos anteriores. Desprecie el rozamiento en todos los casos.
Para los dos casos anteriores calcule la fuerza de reacción cuando el vector de posición de la partícula forma un ángulo θ con la dirección vertical hacia abajo.
Anilla en aro con resorte
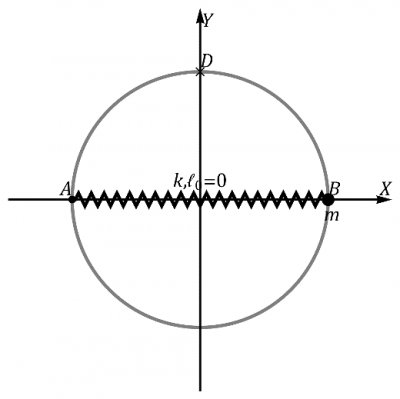
Una pequeña anilla de masa m se encuentra ensartada en un aro de radio R, situado horizontalmente (es decir, en este problema el peso no desempeña ningún papel). La anilla puede moverse sobre el aro sin rozamiento. La anilla se ecuentra unida a un resorte de constante k y longitud natural nula, , estando su otro extremo atado a un punto fijo del aro (es decir, el muelle ejerce una fuerza , siendo A el extremo fijo y P la posición de la partícula.
Situamos los ejes de manera que el centro coincide con el origen y el punto fijo del resorte está en . La particula se encuentra inicialmente en reposo en el punto diametralmente opuesto
. Entonces se le comunica una muy ligera velocidad en la dirección de
- Calcule la fuerza de reacción que ejerce el aro cuando la anilla se encuentra en su posición inicial.
- Calcule la velocidad de la anilla y la fuerza de reacción del aro cuando, en su movimiento, pasa por el punto diametralmente opuesto, A.
- Calcule la velocidad de la anilla y la fuerza de reacción del aro cuando, en su movimiento, pasa por el punto D, situado a medio camino entre B y A.
- Calcule la velocidad de la anilla y la fuerza de reacción del aro cuando, en su movimiento, pasa por un punto P tal que el ángulo que forma el vector de posición respecto al centro con el eje OX es θ.
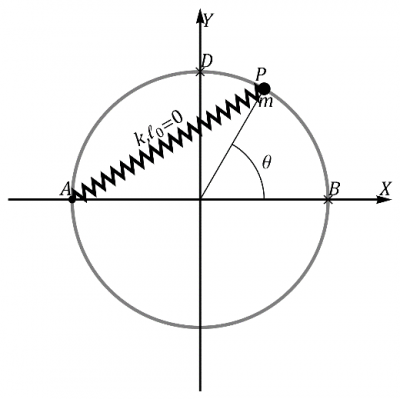
Partícula que se despega de esfera
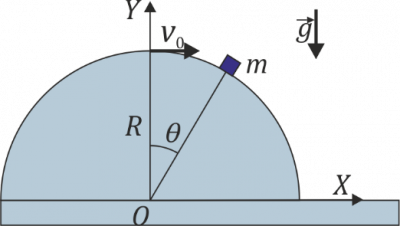
Una partícula de masa se encuentra en lo alto de una cúpula hemisférica de radio , sobre la cual la masa puede deslizar sin rozamiento. La semiesfera está rígidamente unida a una superficie horizontal. La masa está sometida a la acción del peso. Estando en esta posición se le comunica una velocidad horizontal de rapidez
- Supóngase en primer lugar que
- Determine el punto de la esfera en el que la partícula se despega de ella.
- ¿Qué rapidez tiene la partícula en el momento en que impacta con el suelo?
- Supongamos ahora una cierta rapidez inicial .
- Determine el punto en el que la masa despega de la superficie esférica, dando el ángulo θ que el vector de posición relativa al centro de la esfera forma con la vertical.
- ¿Cuál es el valor mínimo de para que la partícula despegue directamente de la superficie, sin deslizar sobre ella?
- Para este valor mínimo de determine la distancia al centro de la semiesfera del punto de la superficie horizontal en el que impacta la partícula.
Velocidad de escape
Se define la velocidad de escape de un campo gravitatorio como aquella que permite llegar al infinito con velocidad nula. Sabiendo que la energía potencial gravitatoria tiene la expresión
- Determine la velocidad de escape que debe tener un cuerpo para salir de un campo gravitatorio hacia el espacio exterior si inicialmente se encuentra a una distancia del centro del planeta.
- Halle los valores numéricos para el caso de la superficie terrestre, la lunar y la marciana. Calcule asimismo el valor para el caso de un satélite situado a la misma distancia del Sol que la Tierra y que desea escapar del campo gravitatorio de aquél.
- Determine el radio que debería tener el Sol para que ni la luz pudiera escapar de él.
Órbita planetaria
Un planeta de masa m se mueve en el campo gravitatorio de una estrella de masa M. Su distancia en el perihelio es r y en el afelio es R. Aplicando la conservación de la energía y del momento cinético, calcule la velocidad del planeta en el perihelio y el afelio.
Disipación de energía en un plano inclinado
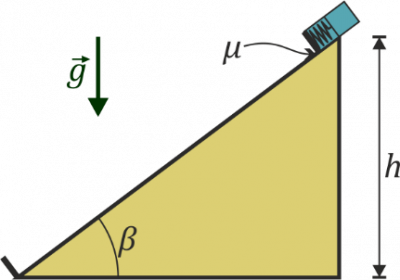
Un bloque de 500 g se encuentra en lo alto de un plano inclinado de 120 cm de altura y una pendiente del 75%. En el extremo inferior del plano se encuentra un resorte que hace rebotar a la masa elásticamente (sale con la misma rapidez con la que llega). Se suelta la masa, dejándola deslizarse por el plano.
- Suponga que no hay rozamiento entre la masa y el plano. ¿Con qué rapidez llega al punto más bajo? ¿Hasta que altura vuelve a subir tras rebotar en el resorte?
- Suponga ahora un coeficiente de rozamiento (estático y dinámico)
- ¿Cuál es la rapidez al llegar al punto más bajo del plano?
- ¿Cuánta energía se ha disipado en el descenso?
- ¿Hasta que altura vuelve a ascender tras el rebote? ¿Cuánta energía se disipa en el ascenso?
- Represente el comportamiento del bloque en una curva de potencial, empleando como energía potencial la gravitatoria.
Masa con resorte en plano inclinado
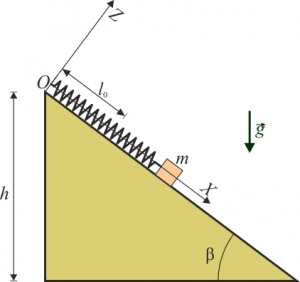
Un bloque de peso se encuentra sobre un plano inclinado de altura y pendiente del 75%. El bloque se encuentra atado al punto superior del plano por un resorte de constante y longitud natural . Para hacer el estudio se considera el sistema de ejes indicado en la figura.
- Suponiendo que no existe rozamiento entre el bloque y el plano, determine la distancia a la que la masa se queda en equilibrio.
- Suponga que inicialmente el bloque se encuentra sujeto a una distancia igual a la longitud natural del resorte y en ese momento se suelta. ¿Cuánto vale su rapidez cuando pasa por la distancia de equilibrio ? ¿Cuál es la distancia máxima a la que llega el bloque?
Potencia de un automóvil
El rozamiento que experimenta un automóvil en movimiento rectilíneo depende de múltiples factores y en un determinado rango de velocidades entre 90 km/h y 130 km/h puede suponerse que la fuerza de rozamiento es lineal con la velocidad . Supongamos un automóvil de 1500 kg que marcha por una carretera horizontal. Se conoce que la potencia que desarrolla para vencer la fricción es de 20 kW (26.8 CV) a 90 km/h y de 35 kW (46.9 CV) a 126 km/h
- Demuestre detalladamente que y que .
- Supongamos que este coche debe ascender una pendiente del 6% (medida como la tangente del ángulo). ¿Qué potencia debe desarrollar a 90 km/h? ¿Y a 108 km/h?
- Si el coche desciende por una cierta pendiente del 6%, ¿a qué velocidad de descenso no es necesario ni acelerar ni frenar el coche?
- Supongamos que se acelera el coche uniformemente desde 90 km/h a 126 km/h empleando para ello una distancia de 500 m, ¿qué aceleración tiene el coche? ¿Cuánto es el trabajo total realizado sobre él en este incremento de velocidad? ¿Qué trabajo realiza el motor del coche en este incremento de velocidad?
Tómese
Movimiento de carga en campo eléctrico
Una partícula cargada de masa 0.01 kg debe atravesar un campo eléctrico localizado en una zona del espacio, de forma que en su movimiento experimenta una fuerza tal que
con y . La partícula se mueve sobre el eje OX, partiendo de con velocidad .
- ¿Llega la partícula hasta ?
- Si es así, ¿cuál es su rapidez cuando pasa por ese punto? ¿Cuál es la velocidad media del trayecto?
- Si no es capaz de llegar hasta , ¿cuál es el valor máximo de x al que llega? ¿Cuánto vale su rapidez cuando vuelve a pasar por ?
- Repita la respuesta estas preguntas para el caso de una partícula de la misma masa pero carga opuesta, es decir, cambiando q por −q.
Caso de fuerza dependiente de la posición
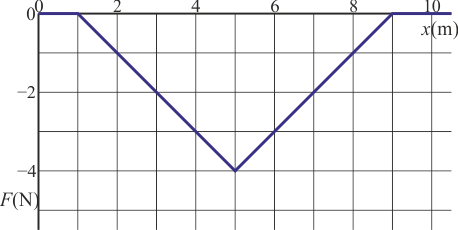
Una partícula de masa 2 kg se mueve por el eje OX de forma que cuando pasa por su velocidad es +3 m/s. Sobre la partícula actúa una fuerza en la dirección del mismo eje, cuya gráfica es la de la figura.

|
|
| (a) | (b) |
|---|
- ¿Cuál es la velocidad de la partícula cuando pasa por ?
- ¿Cuál será la respuesta a la pregunta anterior si la fuerza es la de la gráfica (b)?
- ¿Cómo es, en cada caso, la gráfica de la energía potencial, si U(0)=0?
Caso de movimiento debido a una fuerza conservativa
Una partícula de masa se mueve a lo largo del eje OX, sometida a la acción de una fuerza conservativa cuya energía potencial es la de la gráfica. Inicialmente se encuentra en moviéndose hacia el semieje OX negativo con rapidez .
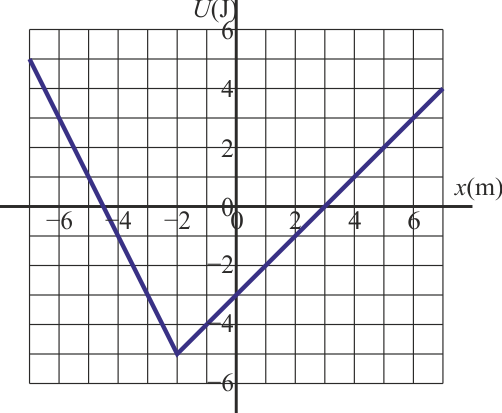
- ¿En qué punto se detiene por primera vez?
- ¿Qué tipo de movimiento describe la partícula desde el punto inicial hasta el punto de retorno?
- ¿Es el movimiento periódico? Si es así, ¿cuánto dura el periodo del movimiento?
- Suponga que la masa se ve sometida adicionalmente a una fuerza de rozamiento que la va frenando hasta detenerla por completo. ¿Cuánta energía se disipa hasta que se detiene?
Caso de curva de potencial
Una partícula de masa 1.5 kg se mueve sobre el eje OX sometida exclusivamente a una fuerza conservativa siendo su energía potencial la de la figura. La partícula parte de soltándose desde el reposo.
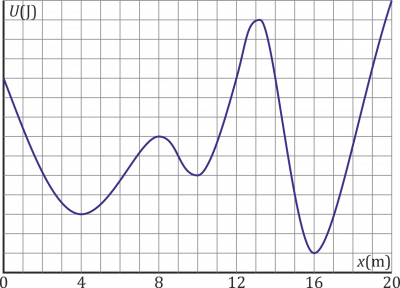
- ¿Dónde se detiene por primera vez?
- ¿En qué punto es máxima su energía cinética? ¿Cuánto vale esta?
- ¿En qué puntos es nula su aceleración? ¿Cuánto vale su rapidez en estos puntos?
- ¿Qué velocidad mínima debe comunicarse a la partícula en x=0 si debe llegar hasta x=16 m? ¿Qué velocidad tiene al pasar por ese punto? ¿Dónde se detiene en ese caso?
Energía potencial función de la posición
Una partícula se mueve por el eje OX sometida a una energía potencial de la forma (en el SI)
- ¿En qué zonas del eje OX la fuerza va hacia la derecha y en cuales hacia la izquierda?
- ¿Dónde están los posibles puntos de equilibrio? ¿Son estables o inestables?
- ¿Cuál de los dos puntos de equilibrio estable es el más estable de los dos (esto es, el que tiene un pozo más profundo)?
















































