Problemas de dinámica de los sistemas y del sólido rígido

Centro de masas de un sistema de dos masas

En un sistema formado por dos masas $m_{A}$ y $m_{B}$ situadas en los extremos A y B de una varilla sin masa de longitud b.

1. ¿Cuál es la posición del centro de masas, CM?
2. ¿Cuánto vale el momento de inercia respecto a un eje perpendicular a la varilla por el CM del sistema?

Solución

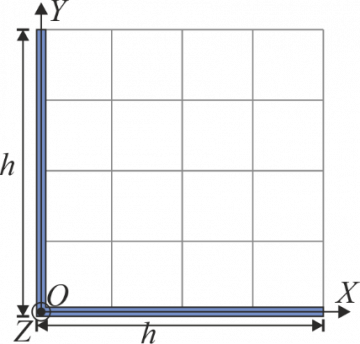
Sólido en forma de L

Se tiene un sólido en forma de L con los brazos de igual longitud b, siendo m la masa total del sólido, distribuida uniformemente. Considerando un sistema de ejes con origen en el vértice y ejes OX y OY paralelos a los brazos de la L.

1. ¿dónde se encuentra en centro de masas del sólido?
2. Calcule el momento de inercia de la L respecto al eje OX y respecto al eje OZ.
3. Calcule el momento de inercia de la L respecto a dos ejes paralelos a OX y OZ pero que pasan por el CM del sólido.

Solución

8 partículas en los vértices de un cubo

Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista b. Halle el momento de inercia del cubo respecto a los siguientes ejes:

1. Uno perpendicular a una cara y que pase por el centro del cubo.
2. Uno que pase por dos vértices opuestos.
3. Uno que pase por los centros de dos aristas opuestas.
4. Uno que pase por una arista.

Solución

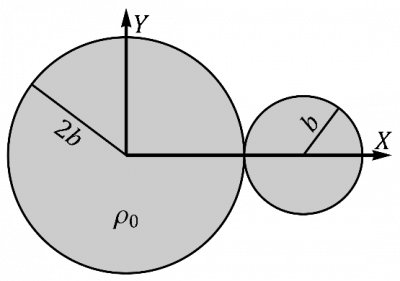
Dos esferas adyacentes

Se tiene un sólido, cuya masa total es m, formado por dos esferas macizas del mismo material de densidad homogénea, una de ellas de radio 2b y la otra de radio b. Las dos esferas son adyacentes.

1. Determine la posición del centro de masas del sistema.
2. Calcule el momento de inercia de este sólido respecto a los siguientes ejes:
   1. Un eje OX que pasa por los centros de las dos esferas
   2. Un eje OY perpendicular al anterior por el centro de la esfera grande
   3. Un eje GY paralelo a OY y que pasa por el CM del sólido

Dato: momento de inercia de una esfera maciza respecto a un eje por su centro: $I=2mR^{2}/5$

Solución

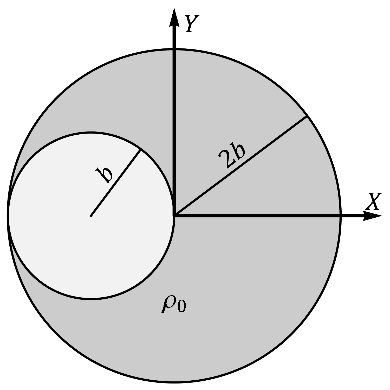
Esfera con hueco esférico

Si en lugar del sistema del problema “Dos esferas adyacentes” se tiene un sólido de masa m en forma de una sola esfera maciza de radio 2b y densidad homogénea en la que se ha horadado una cavidad también esférica, de radio b, cuyo centro se encuentra a una distancia b del centro de la esfera original.

1. ¿Dónde se halla el centro de masas del sólido?
2. Calcule el momento de inercia de este sólido respecto a los siguientes ejes:
   1. Un eje OX que pasa por los centros de las dos esferas.
   2. Un eje OY perpendicular al anterior por el centro de la esfera grande.
   3. Un eje GY paralelo a OY y que pasa por el CM del sólido.

Solución

Momento de inercia de sólidos cilíndricos

Halle los siguientes momentos de inercia de sólidos de densidad homogénea:

1. Una superficie cilíndrica hueca, de masa m, radio R y altura h.
2. Un cilindro macizo, de masa m, radio R y altura h.
3. Una corona cilíndrica de masa m, radio interior $R_{1}$ y exterior $R_{2}$, con altura h.

En todos los casos, el momento de inercia debe hallarse respecto al eje del cilindro.

Solución

Momento de inercia de una esfera maciza

Halle el momento de inercia de una esfera maciza homogénea respecto a un eje que pasa por su centro (sugerencia, descomponga la esfera en una pila de discos).

Solución

Momento cinético de una máquina de Atwood

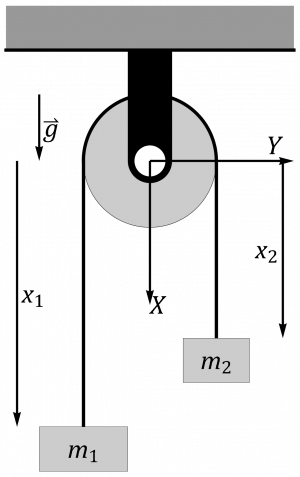
Considere una máquina de Atwood ideal formada por dos masas $m_{1}$ y $m_{2}$ que cuelgan de una polea (ideal, sin rozamiento ni masa) de radio b, a través de un hilo también ideal (inextensible y sin masa) de longitud $\ell$. Inicialmente las dos masas están en reposo a la misma altura.

1. Determine la masa total, la posición, velocidad y aceleración del centro de masas, la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética del sistema, todo ello como función del tiempo.
2. A partir del teorema del momento cinético, calcule la aceleración que adquieren las dos masas.
3. Para la cantidad de movimiento, el momento cinético respecto al centro de la polea y la energía cinética determine sus derivadas respecto al tiempo y compruebe que se satisfacen las leyes para su evolución.

Solución

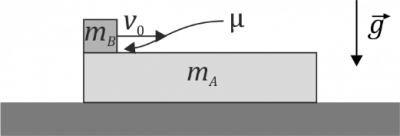
Disipación de energía de un sistema por fricción

Supongamos dos bloques de masas $m_{A}$ y $m_{B}$ puestos el uno encima del otro y el inferior sobre una superficie horizontal sin rozamiento. Inicialmente el bloque A, el inferior, está inmóvil, mientras que el B, el superior se le comunica inicialmente una velocidad $v_{0}{\vec {\imath }}$ Hay un coeficiente de rozamiento dinámico μ entre los dos bloques.

1. ¿Cómo se mueven a partir de ese momento cada una de las masas?
2. ¿Cómo se mueve el centro de masas?
3. ¿Cómo cambia la cantidad de movimiento del sistema con el tiempo?
4. ¿Cómo cambia la energía cinética con el tiempo?

Solución

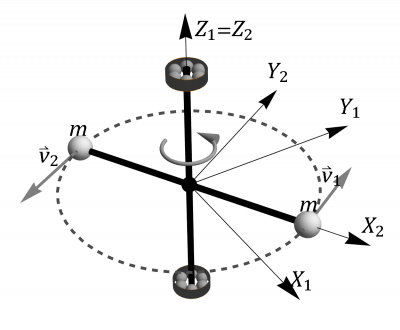
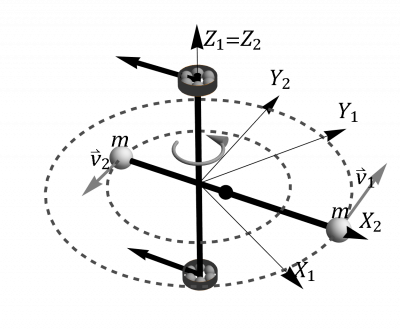
Rotor formado por dos masas

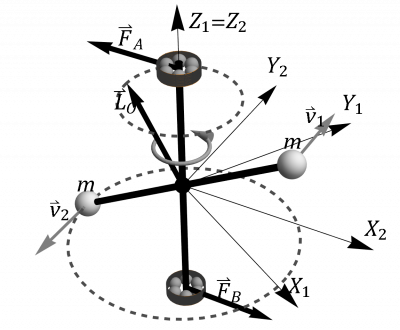
Se tiene un rotor formado por dos masas iguales de valor $m_{0}$ situadas en los extremos de una barra ideal (sin masa) de longitud H. Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia h del centro de la barra (uno por encima, en A y otro por debajo de ella, en B).

Calcule la cantidad de movimiento, el momento cinético y la energía cinética respecto al punto fijo O donde la varilla está soldada al eje, si el rotor gira con velocidad angular ω en torno al eje cuando

1. Es horizontal y se encuentra centrado en el eje vertical.
2. Es horizontal, pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste).
3. Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β.
4. Es horizontal y se encuentra centrado en el eje vertical, pero las masas no son exactamente iguales, sino que valen $m_{1}$ y $m_{2}$.

Solución

Equilibrio de una tabla con tirante

Una mesa plegable está articulada a la pared por un extremo, y cuelga de la pared por un cable tirante. En dos dimensiones esto se puede modelar como una barra de longitud b y masa m distribuida uniformemente. La barra está articulada por su extremo A y atada por su extremo B a una pared vertical, de forma que el cable forma un ángulo de 45° con la vertical. Calcule la tensión del cable, así como la fuerza de reacción en el punto A.

Solución

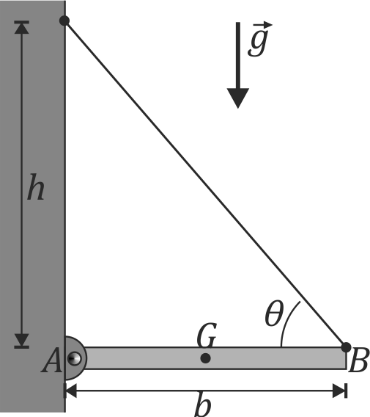
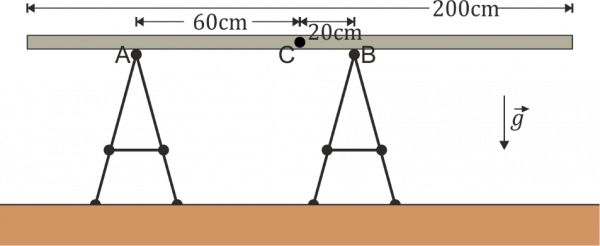
Tabla apoyada sobre dos patas

Se tiene una plataforma de masa $m=6.0\,\mathrm {kg}$ y longitud $b=2.00\,\mathrm {m}$ (estando la masa distribuida uniformemente) que se apoya horizontalmente sobre dos caballetes de forma que los puntos de apoyo A y B están a 60 cm y 20 cm del centro C de la tabla, respectivamente.

1. Calcule la fuerza que cada caballete ejerce sobre la tabla.
2. Halle el valor máximo de la masa que se puede apoyar en el borde izquierdo de la plataforma si no se quiere que esta vuelque.

Tómese $g=10\,\mathrm {m} /\mathrm {s} ^{2}$.

Solución

Fuerza aplicada sobre una barra

Sobre una barra AB homogénea de longitud b y masa m situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza $F_{0}$ también horizontal. El punto de aplicación P se encuentra a una distancia c del centro de la barra, G.

1. Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
2. Suponga ahora que la fuerza forma un ángulo β con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
3. Suponga que la barra se encuentra articulada en su extremo A de forma que sólo puede girar en torno a este punto. Para la misma fuerza del apartado anterior ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
4. Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto valdrían la fuerza y el momento de reacción ejercidos por el soporte si se aplica la misma fuerza de los apartados anteriores?

Solución

Movimiento de péndulo compuesto

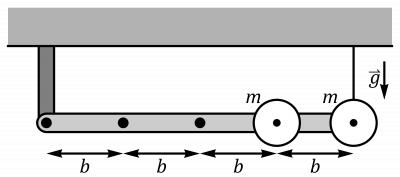
Se construye un péndulo compuesto mediante una barra muy ligera de longitud 4b, con orificios espaciados una distancia b. Se dispone de dos pesas de la misma masa m.

1. En primer lugar, se sitúan las masas en los orificios 4º y 5º y la varilla se cuelga del techo mediante una barra articulada en el primer orificio. El otro extremo se encuentra unido al techo por un hilo.
   1. Calcule la tensión del hilo y la de la barra en el estado de equilibrio.
   2. Suponga ahora que se corta el hilo. Para el instante inmediatamente posterior al corte, halle
      1. la aceleración lineal de cada masa,
      2. la tensión del soporte
      3. la tensión de cada tramo de la varilla.
2. En segundo lugar, se sitúan las masas en los orificios 1º y 5º y se suspende del 2º. Responda de nuevo a las mismas cuestiones.

  

Solución

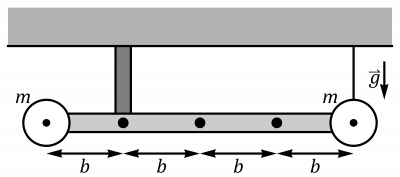
Máquina de Atwood con momento de inercia

Dos masas $m_{1}$ y $m_{2}$ están unidas por una cuerda ideal, inextensible y sin masa Esta cuerda pasa por una polea con momento de inercia I respecto a su eje. La polea no tiene rozamiento que le impida girar en torno a su eje. Determine la aceleración con la que se mueven las masas, las tensiones en cada tramo de la cuerda, así como la fuerza en el punto de anclaje de la polea.

Solución

Rodadura con deslizamiento

Por un suelo horizontal se lanza un disco macizo de masa m y radio R. Inicialmente el centro del disco avanza con velocidad $v_{0}{\vec {\imath }}$ y el disco gira con velocidad angular $\omega _{0}{\vec {k}}$, de manera que desliza además de rodar. El coeficiente de rozamiento dinámico con el suelo vale μ.

1. Determine la aceleración lineal del centro del disco y la aceleración angular del disco.
2. Halle la velocidad lineal del centro del disco, la velocidad angular del disco y la velocidad lineal del disco en el punto de contacto con el suelo como funciones del tiempo
3. ¿Cuánto tarda el disco en dejar de deslizar y empezar a rodar sin deslizar?
4. ¿Cómo es el movimiento una vez que empieza a rodar sin deslizar? ¿Cuál debe ser la velocidad angular inicial mínima para que el disco retorne al lanzador?
5. Estudie como varían en el tiempo la energía cinética de traslación, de rotación y la total.

Solución

Descenso rodante por un plano inclinado

En lo alto de un plano inclinado de altura h y con una cierta inclinación β se encuentran los siguientes objetos:

• una superficie cilíndrica hueca,
• un cilindro macizo,
• una superficie esférica hueca
• una esfera maciza.

1. Si se sueltan a la vez desde el extremo superior del plano, ¿dependerá el orden de llegada de la masa y el radio de cada uno? ¿con qué rapidez del CM llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuánto tarda cada uno en llegar?
2. Si el coeficiente de rozamiento entre los sólidos y el suelo vale μ, ¿cuál debe ser la pendiente máxima que debe tener el plano si no deslizan? A medida que se va aumentando la inclinación del plano, ¿en qué orden empiezan a deslizar?

Solución

Rodadura con fuerzas y momentos

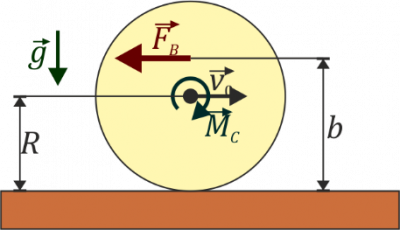
Un disco homogéneo de masa m y radio R rueda sin deslizar sobre una superficie horizontal. Inicialmente el centro del disco avanza con una velocidad $v_{0}{\vec {\imath }}$. Al movimiento del disco se opone una fuerza constante ${\vec {F}}_{B}=-F_{0}{\vec {\imath }}$ que actúa sobre un punto B a una altura b sobre el suelo.

1. Determine el par ${\vec {M}}_{C}$ que debe ejercer un motor sobre el eje del disco para que éste mantenga su velocidad constante. ¿Cuánto vale en ese caso la fuerza sobre el disco en el punto de contacto con el suelo?
2. Si en el estado anterior deja de actuar el motor, pero se mantiene la fuerza aplicada ${\vec {F}}_{B}$, ¿cuánto vale la aceleración del centro del disco? ¿Y la aceleración angular del disco? ¿Y la fuerza en el punto de contacto?
3. Si volviendo al caso del primer apartado, deja de actuar la fuerza externa pero se mantiene el momento ${\vec {M}}_{C}$ aplicado en el eje con su valor calculado en dicho apartado ¿cuánto vale la aceleración del centro del disco? ¿Y la aceleración angular del disco? ¿Y la fuerza en el punto de contacto?
4. Si el coeficiente de rozamiento estático entre la rueda y el suelo vale μ, ¿cuál es valor máximo de $F_{0}$ para que la rueda no deslice en los apartado anteriores?

Solución

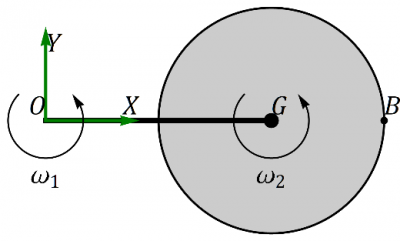
Giro de disco ensartado en varilla

Se tiene una varilla horizontal de masa despreciable y longitud 2R. Un extremo de la varilla se encuentra fijo en el origen de coordenadas, O. La varilla gira en torno al eje OZ con velocidad angular constante ${\vec {\omega }}_{1}=3\omega _{0}{\vec {k}}$. En el otro extremo, G, de la varilla se encuentra ensartado un disco homogéneo de masa m y radio R, también horizontal. El disco gira con velocidad angular constante ${\vec {\omega }}_{2}=2\omega _{0}{\vec {k}}$ alrededor de un eje paralelo a OZ por G. En un momento dado, la varilla se encuentra alineada con el eje OX. Para ese instante…

1. ¿Cuánto vale la velocidad de B, el punto del disco situado en el extremo del disco opuesto a O?
2. ¿Cuánto vale la aceleración de B, el punto del disco situado en el extremo del disco opuesto a O?
3. ¿Dónde se encuentra el centro instantáneo de rotación del disco?
4. ¿Cuánto vale la cantidad de movimiento del disco?
5. ¿Cuánto vale el momento cinético del disco respecto al punto O?
6. ¿Cuánto vale la energía cinética del disco?
7. ¿Cuánto vale la fuerza que se aplica en O para mantener el sistema en movimiento?
8. ¿Cuánto vale el momento resultante que se aplica en O para mantener el sistema en movimiento?

Solución

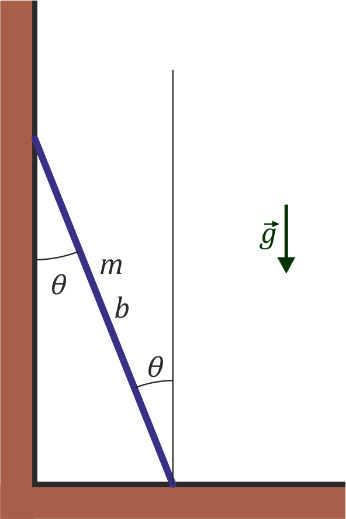
Descenso de una barra apoyada en pared y suelo

Supongamos que tenemos una barra de masa m y longitud b apoyada en el suelo y en una pared vertical, sometida a la acción del peso (vertical y hacia abajo) y a las fuerzas de reacción en los puntos de contacto.

1. Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la pared. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
2. Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?
3. En una posición de equilibrio del apartado anterior, ¿cuánto valen las fuerzas de reacción normales en la pared y el suelo?

Solución

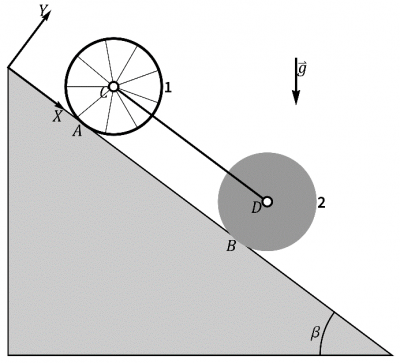
Dos rodillos en plano inclinado

Se tiene un sistema formado por dos rodillos. Uno de ellos (“1”) es un aro de radio $R=0.5\,\mathrm {m}$ y masa $m_{1}=1\,\mathrm {kg}$. El aro posee unos radios de masa despreciable. El segundo sólido (“2”) es un disco homogéneo del mismo radio $R=0.5\,\mathrm {m}$ y masa $m_{2}=4\,\mathrm {kg}$. Los dos cuerpos están unidos por una varilla rígida de masa despreciable, articulada en sus centros. Se sitúan los dos cuerpos sobre un plano inclinado un ángulo con una pendiente $\tan(\beta )=3/4$. El coeficiente de fricción estática y dinámica, $\mu =0.5$, es lo bastante alto como para que ambos cuerpos rueden sin deslizar. Consideramos un sistema de referencia en el que el eje OX es paralelo al plano y el eje OY perpendicular a él. Sean A y B los puntos de contacto de ambos cuerpos con el plano, y C y D los centros respectivos. Suponemos $g=10\,\mathrm {m} /\mathrm {s} ^{2}$ y medimos todo en las unidades fundamentales del SI.

1. ¿Cuánto vale la aceleración de los centros de ambos cuerpos, en m/s^2 ?
2. ¿Cuánto vale la fuerza sobre cada cuerpo en el punto de contacto con el suelo, en N?
3. ¿Cuánto vale la tensión de la varilla que une los centros, en N?
4. En el descenso por el plano, la energía potencial del sistema se reparte entre los dos cuerpos en forma de energía cinética. En cada instante, ¿qué fracción de la energía cinética total tiene el aro y cuál el disco?
5. ¿Cuál debe ser el valor mínimo del coeficiente de rozamiento con el suelo si no se desea que ninguno de los dos cuerpos deslice?

Solución