Problemas de Introducción a la Mecánica Analítica (MR G.I.C.)
Problemas del boletín
Dos barras en V con apoyos
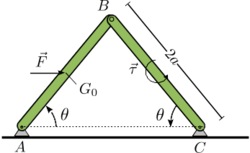
el Principio de los Trabajos Virtuales, determina las reacciones horizontal y vertical en el punto para la estructura de la figura. La masa de las barras es despreciable. Calcula el valor numeŕico para los valores , , , .
Barra articulada colgando de muelle
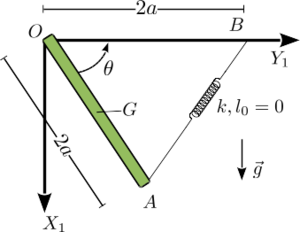
Una barra de longitud esta articulada en su extremo . En el otro extremo (punto ) se conecta un muelle de constante elástica y longitud natural nula. El otro extremo del muelle se coloca en un punto fijo sobre el eje .
- Determina el valor del ángulo para la posición de equilibrio.
- Calcula la fuerza en la dirección del eje sobre el punto en la situación de equilibrio.
- Supongamos que liberamos el punto , de modo que puede deslizar por el eje sin rozamiento. Encuentra la configuración de equilibrio en este caso.
- ¿Como se podría resolver el problema de equilibrio si incluimos rozamiento en el contacto de con el eje ?
Otros problemas
Equilibrio de armadura con muelle
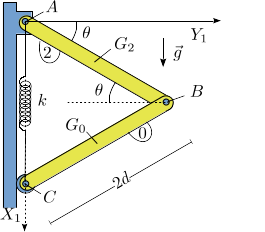
En el sistema de la figura las barras tienen longitud y masa cada una. La barra "2" está articulada en el punto fijo , mientras que el extremo de la barra "0" puede deslizar sin rozamiento sobre la superficie vertical. El muelle que conecta los puntos y tiene constante elástica y longitud natural nula. El muelle se mantiene siempre vertical. La gravedad actúa como se indica en la figura.
- Calcula la energía potencial del sistema.
- Suponiendo que el muelle se ajusta de modo que , determina los valores de para los que hay equilibrio mecánico. Discute la estabilidad de estas posiciones de equilibrio.
- Si se aplica una fuerza sobre el punto , con , determina el nuevo valor de para que haya equilibrio mecánico.
Equilibrio de barra con muelle
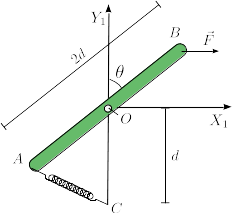
Una barra de longitud está articulada en su punto central en el punto fijo . El extremo se conecta al punto fijo por un muelle de constante elástica y longitud natural nula. Una fuerza , con , se aplica en el punto . No se tiene en cuenta la fuerza de la gravedad.
- Usando el Principio de los Trabajos Virtuales (PTV) (o el de las potencias virtuales, PPV) determina el valor de equilibrio del ángulo .
- Si el ángulo es tal que y , determina, usando el Principio de Liberación y el PTV (o el PPV), las componentes de la fuerza de reacción vincular en (en la base de los ejes de la figura)




















