Principios de la electrostática (GIOI)

Ley de Coulomb

La ley de Coulomb fue descubierta por Henry Cavendish, que no lo publicó. Varios años después, Coulomb redescubrió esta ley, publicándolo adecuadamente, por lo que recibe su nombre.

Es una ley física que nos describe la fuerza entre dos cargas puntuales en reposo. Nos dice que si tenemos dos cargas puntuales $q_{1}$ y $q_{2}$ situadas a una distancia $d_{12}$, aparece una fuerza eléctrica entre ellas tal que:

Módulo

• es proporcional al producto de las cargas.
• es inversamente proporcional al cuadrado de la distancia entre las cargas.

Dirección

Es la de la recta que pasa por las dos cargas

Sentido

Depende del signo de las cargas

• Cargas del mismo signo se repelen
• Cargas de distinto signo se atraen

Matemáticamente esto se expresa como que la fuerza que produce la carga 1 sobre la 2 es

${\vec {F}}_{1\to 2}=k_{e}{\frac {q_{1}q_{2}}{d_{12}^{2}}}{\vec {u}}_{12}$

siendo ${\vec {u}}_{12}$ el vector unitario en la dirección de la recta que pasa por las dos cargas y lleva el sentido de la 1 a la 2, es decir, hacia fuera de las dos cargas. La fuerza que la 2 produce sobre la 1 se calculará del mismo modo, sustituyendo ${\vec {u}}_{12}$ por ${\vec {u}}_{21}$ que es el unitario opuesto.

    

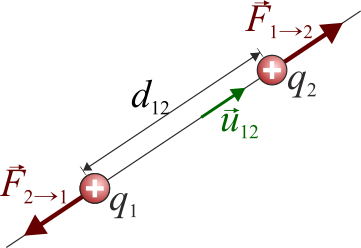
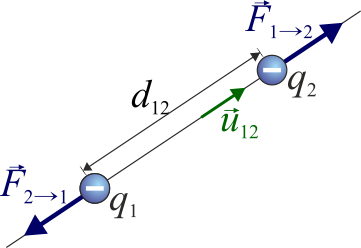
Esta expresión es válida tanto si las cargas son del mismo signo como si son de signos opuestos. En el segundo caso, el producto de las cargas es negativo y resulta una fuerza atractiva.

La constante $k_{e}$ universal que, por la forma en que se eligen las unidades en el SI tiene un valor

$k_{e}=8.986851134(13)\times 10^{9}{\frac {\mathrm {N} \cdot \mathrm {m} ^{2}}{\mathrm {C} ^{2}}}\simeq 9\times 10^{9}{\frac {\mathrm {N} \cdot \mathrm {m} ^{2}}{\mathrm {C} ^{2}}}$

siendo el segundo valor mucho más fácil de recordar y con un error de solo el 0.1%.

Esta constante de proporcionalidad suele escribirse en la forma aparentemente más complicada

$k_{e}={\frac {1}{4\pi \varepsilon _{0}}}\qquad \Rightarrow \qquad \varepsilon _{0}={\frac {1}{4\pi k_{e}}}\simeq 8.854\times 10^{-12}{\frac {\mathrm {C} ^{2}}{\mathrm {N} \cdot \mathrm {m} ^{2}}}=8.854{\frac {\mathrm {pF} }{\mathrm {m} }}$

La razón de escribirlo de esta forma se halla en la ley de Gauss.

Si lo que conocemos son los vectores de posición de las dos cargas respecto a un sistema de referencia, podemos escribir la ley de Coulomb en función de estos vectores, ya que

$d_{12}=\left|{\vec {r}}_{2}-{\vec {r}}_{1}\right|\qquad \qquad {\vec {u}}_{12}={\frac {{\vec {r}}_{2}-{\vec {r}}_{1}}{\left|{\vec {r}}_{2}-{\vec {r}}_{1}\right|}}$

y queda

${\vec {F}}_{1\to 2}={\frac {1}{4\pi \varepsilon _{0}}}\,{\frac {q_{1}q_{2}({\vec {r}}_{2}-{\vec {r}}_{1})}{|{\vec {r}}_{2}-{\vec {r}}_{1}|^{3}}}$

Hay que destacar (porque es fuente de errores) el cambio del exponente del denominador de 2 a 3, al introducir una distancia más en la normalización del vector de posición relativo.

Como ilustración de la magnitud la fuerza eléctrica podemos considerar la atracción entre un protón y un electrón que se hallan a una distancia de un radio de Bohr (tamaño del átomo de hidrógeno)

$|q_{p}|=|q_{e}|=e=1.602\times 10^{-19}\mathrm {C} \qquad a_{0}=5.29\times 10^{-11}\,\mathrm {m}$

Resulta un módulo de la fuerza

$|{\vec {F}}|=k_{e}{\frac {e^{2}}{a_{0}^{2}}}={\frac {9\times 1.6^{2}}{5.29^{2}}}\times 10^{9-19-19+11+11}\mathrm {N} =8.24\times 10^{-8}\,\mathrm {N}$

Esta fuerza no parece excesivamente intensa, pero debemos tener en cuenta que actúa sobre un electrón, cuya masa es minúscula. La aceleración que produce esta fuerza es

$|{\vec {a}}|={\frac {|{\vec {F}}|}{m}}={\frac {8.24\times 10^{-8}}{9.1\times 10^{-31}\mathrm {kg} }}=9.04\times 10^{22}{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}=9.22\times 10^{21}g$

Dicho de otra forma, la fuerza debida a un solo protón es 9000000000000000000000 veces la atracción gravitatoria debida a la Tierra entera.

Otra comparación posible es la de la fuerza eléctrica entre el protón y el electrón y la fuerza gravitatoria entre ellas. Su cociente vale

${\frac {F_{e}}{F_{g}}}={\frac {k_{e}q_{1}q_{2}/d^{2}}{Gm_{1}m_{2}/d^{2}}}={\frac {k_{e}e^{2}}{Gm_{e}m_{p}}}=2.3\times 10^{39}$

es decir, la fuerza eléctrica es 2300000000000000000000000000000000000000 veces más intensa que la gravitatoria.