Primera Prueba de Control 2019/20 (G.I.C.)

De Laplace

1 Masa en aro con muelle

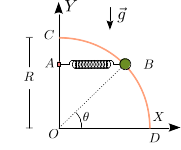
Una partícula de masa m está obligada a moverse a lo largo de un hilo delgado circular de radio R, como se indica a la figura. La partícula está conectada a un muelle de constante elástica k y longitud natural nula. El punto de anclaje A del muelle puede moverse sobre el eje OY, de modo que el muelle siempre permanece horizontal. El contacto entre la partícula y el hilo es rugoso, con coeficiente de rozamiento estático μ.

1. Dibuja el diagrama de fuerzas de la partícula. Indica de que fuerzas es conocido su sentido antes de resolver el problema
2. ¿Cómo es la fuerza que el muelle ejerce sobre la partícula?. ¿Y la fuerza de rozamiento?
3. Supongamos ahora que se cumple mg = F₀ / 5 y kR = F₀ / 3, siendo F₀ una constante dada. Calcula el módulo de la fuerza normal sobre la partícula en condiciones de equilibrio estático si el ángulo θ es tal que
4. ¿Cuánto debe valer el coeficiente de rozamiento estático para que la situación descrita sea posible?

2 Masas con cuerda horizontal

Las masas puntuales m₁ y m₂ se deslizan sin rozamiento sobre una superficie horizontal. Las masas están unidas por una cuerda ideal, inextensible y sin masa, de longitud L. Una fuerza actúa sobre la masa m₁. Las masas se mueven de modo que la cuerda está siempre tensa.

1. Calcula la tensión de la cuerda durante el movimiento
2. Supongamos ahora que las dos masas son iguales, m₁ = m₂ = m₀. En el instante inicial la masa m₂ esta en el punto O y la cuerda está completamente estirada. Las dos masas están en reposo en este instante inicial. Ahora la fuerza depende del tiempo como , siendo A una constante.
   1. Cuáles son las unidades base de A en el S.I.
   2. ¿Cuál es la posición de la masa m₁ en función del tiempo?
   3. En el instante t = t_p la partícula 1 se para súbitamente. ¿Cuanto tiempo tarda en chocar con ella la partícula 2?