Primera Convocatoria Ordinaria 2019/20 (MR G.I.C.)

Dos barras articuladas con muelle

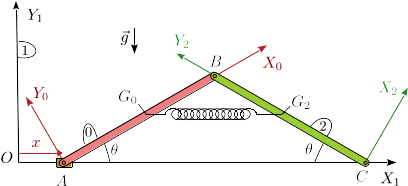
El sistema de la figura consta de dos barra articuladas. La longitud de las dos barras es $L=2b$. La masa de la barra "2" es $m$, mientras que la de la masa "0" es despreciable. Las barras se articulan entre sí en el punto $B$. El extremo $A$ de la barra "0" se conecta con un pasador, de modo que desliza sobre el eje fijo $OX_{1}$. La barra "2" está articulada sobre el eje $OX_{1}$ en el punto fijo $C$. Un muelle de constante elástica $k$ y longitud natural nula conecta los centros de las barras.

1. Determina gráfica y analíticamente la posición de los CIR de los tres movimientos que se pueden definir en el sistema.
2. ¿Cuántos grados de libertad tiene el problema?. Encuentra reducciones cinemáticas de los movimientos $\{21\}$, $\{20\}$ y $\{01\}$. Las reducciones deben expresarse en función de los grados de libertad.
3. Calcula la energía cinética y potencial del sistema.
4. Determina la posición de equilibrio.
5. Se aplica un par ${\vec {\tau }}=\tau _{0}\,{\vec {k}}_{1}$ sobre la barra "2". Dibuja el diagrama de fuerzas y pares que actúan sobre cada barra.
6. Calcula la cantidad de movimiento de cada barra.
7. Calcula ${\vec {L}}_{G_{0}}^{\,'0'}$ y ${\vec {L}}_{C}^{\,'2'}$.
8. Aplicando el T.C.M. y el T.M.C. encuentra las ecuaciones que describen el sistema.
9. Escribe la función de Lagrange y las ecuaciones de Lagrange del sistema.

Percusión sobre una barra vertical

Una varilla delgada (sólido "2") de masa $m$ y longitud $2b$ está articulada en un pasador (punto $A$) que desliza sobre el eje fijo $OY_{1}$.

1. Calcula la reducción cinemática en el punto $A$ del movimiento {21}.
2. Calcula la energía cinética de la varilla y su energía potencial.
3. Cuando la varilla se encuentra en reposo y con $x=0$ y $\theta =0$, se aplica en el punto $C$ una percusión ${\vec {\hat {F}}}={\hat {F}}_{0}\,(-{\vec {\imath }}_{1}+{\vec {\jmath }}_{1})$, con ${\hat {F}}_{0}>0$. Determina el movimiento de la varilla justo después de la percusión así como el valor de la percusión vincular en $A$.
4. Discute el movimiento del punto $A$ en función del valor de $s$. ¿Donde está el centro de percusión de $A$?