Primera Convocatoria Ordinaria 2014/15 (G.I.C.)

Partícula sobre espiral con muelle

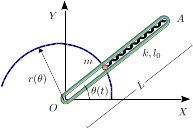
Una partícula de masa $m$ está engarzada en la barra ranurada de la figura. El muelle, de longitud natural $l_{0}<L$ y constante elástica $k$, la empuja de modo que, al girar la barra, la partícula está obligada a moverse sobre la espiral indicada, de ecuación $r(\theta )=r_{0}e^{\theta }$, con $\theta =\theta (t)$. La barra gira de modo que la partícula se mueve con rapidez constante $v_{0}$. El efecto de la gravedad es despreciable.

1. Usando coordenadas polares, escribe las expresiones del vector de posición, velocidad y aceleración de la partícula. Deja el resultado en función de $\theta$ y sus derivadas.
2. Calcula la ley horaria $\theta (t)$.
3. Determina la fuerza que ejerce el muelle sobre la partícula, asi como la energía potencial del muelle. Expresa estos dos resultados en función del ángulo $\theta$.
4. ¿Se conserva la energía mecánica de la partícula? ¿Y el momento cinético respecto a $O$? Razona las respuestas.

Barra apoyada en un escalón

Una barra homogénea, de longitud $L$ y peso $P$, está apoyada sobre un escalón de altura $d$ formando un ángulo $\alpha$ con la horizontal. El contacto en el punto $B$ es liso, mientras que es rugoso en el punto $A$, con un coeficiente de rozamiento estático $\mu$.

1. Dibuja el diagrama de cuerpo libre de la barra.
2. Determina la expresión de las fuerzas que actúan sobre la barra en condiciones de equilibrio estático.
3. Si $\alpha =\pi /4$, qué condición debe cumplir $d$ para que se mantenga el equilibrio? ¿El equilibrio se rompe por deslizamiento o por vuelco? Razona la respuesta.