Primera Convocatoria Ordinaria 2011/12 (G.I.C.)

Péndulo enrollándose alrededor de una clavija delgada

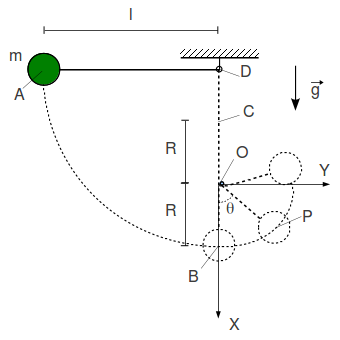
Un péndulo consiste en una pequeña masa $m$ atada al extremo de una cuerda inextensible y sin masa de longitud $l$. La masa se coloca en el plano horizontal y se suelta. En el punto más bajo de la oscilación (punto $B$), la cuerda choca con una clavija delgada (punto $O$) situada a una distancia $R$ por encima de del punto $B$.

1. Para el punto más bajo de la oscilación (punto $B$) calcula el módulo de la velocidad de la masa, su cantidad de movimiento y su momento cinético respecto al punto $D$.
2. Expresa en coordenadas polares la posición respecto del punto $O$ de la masa después de que la cuerda haya chocado con la clavija (punto $P$). Encuentra la expresión de la velocidad y la aceleración de la masa.
3. Para el movimiento de la masa después del punto $B$, encuentra la expresión de la ecuación diferencial que rige la variación del ángulo $\theta$, la expresión que da la tensión de la cuerda y las condiciones iniciales de la ecuación diferencial en el punto $B$.
4. ¿Cuál es la condición que debe cumplir la distancia $R$ para que la masa describa al menos un círculo completo alrededor de la clavija, es decir, para que llegue al punto $C$?

Varilla apoyada sobre dos rampas

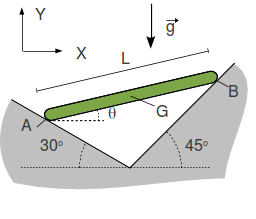
Una barra de longitud $L$ y masa $m$ se apoya sobre dos planos inclinados como se indica en la figura. Los apoyos en los planos son lisos. El peso de la barra se aplica en su centro. Dibuja el diagrama de cuerpo libre de la barra.

1. Calcula las fuerzas de reacción vincular en los apoyos (puntos $A$ y $B$).
2. Calcula el valor del ángulo $\theta$ para el que la barra se encuentra en equilibrio.
3. Consideramos ahora una situación en la que el ángulo $\theta$ vale $\theta =30.0^{\circ }$. En este caso el contacto en $A$ es rugoso mientras que en $B$ es liso. Calcula el valor del módulo de la fuerza de rozamiento en $A$ si la masa de la barra es $m=250\,\mathrm {g}$.