Potencia eléctrica (GIOI)

Flujo de trabajo que entra en un sistema

La transmisión de una corriente eléctrica implica un consumo de energía.

Imaginemos un sistema (no necesariamente óhmico) con dos extremos A y B, situados a potenciales $V_{A}$ y $V_{B}$.

Podemos imaginar que hay una fuente de tensión que sitúa el extremo A a la tensión $V_{A}$. El trabajo realizado por esta fuente en un tiempo $\mathrm {d} t$ es igual a la cantidad de carga que pone a ese potencial multiplicada por la tensión a la que la pone. Ese trabajo entra en el sistema (el cable)

$\delta W_{\mathrm {in} }=\mathrm {d} Q_{A}\,V_{A}$

pero la carga que atraviesa el generador es proporcional a la intensidad de corriente

$\mathrm {d} Q_{A}=I_{A}\,\mathrm {d} t$

siendo $I_{A}$ la corriente que entra en el sistema por el extremo A. Por tanto

$\delta W_{\mathrm {in} }=I_{A}\,V_{A}\,\mathrm {d} t$

Dividiendo por el diferencial de tiempo queda un flujo de trabajo (potencia eléctrica) debido a este generador

${\dot {W}}_{\mathrm {in} }=I_{A}V_{A}$

Para el otro extremo se aplica el mismo razonamiento por lo que el flujo de trabajo total

${\dot {W}}_{\mathrm {in} }=I_{A}V_{A}+I_{B}V_{B}\,$

Más en general, si tenemos un sistema con N terminales por las cuales entra corriente, el flujo de trabajo, es decir, la potencia eléctrica, que entra en el sistema es

$P_{\mathrm {e} }={\dot {W}}_{\mathrm {in} }=\sum _{i}I_{i}V_{i}\,$

donde las $I_{i}$ son las corrientes que entran el sistema por las diferentes terminales. Evidentemente, de acuerdo con la ley de conservación de la carga, algunas de estas corrientes serán negativas.

En particular, si tenemos un sistema con una única entrada y una salida, de forma que la corriente que entra por un cable sale por el otro, se cumple

$I_{A}=I\qquad \qquad I_{B}=-I$

y por tanto

${\dot {W}}_{\mathrm {in} }=I_{A}V_{A}+I_{B}V_{B}=I(V_{A}-I_{B})=I\,\Delta V$

Es decir la potencia eléctrica en un sistema con una entrada y una salida es igual al producto de la intensidad que entra por la d.d.p. entre la entrada y la salida.

Motores eléctricos y generadores eléctricos

La potencia eléctrica o flujo de trabajo eléctrico que penetra en un sistema puede emplearse para distintos objetivos o con diferentes resultados.

Uno de ellos es la realización de trabajo mecánico. Este es el principio de los motores eléctricos. En un motor se consume una potencia eléctrica que en parte se emplea en realizar trabajo y en parte se pierde en forma de calor (por rozamiento y por efecto Joule).

    

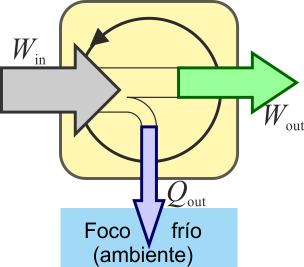
El sistema puede funcionar a la inversa, es decir, puede emplearse trabajo mecánico para producir trabajo eléctrico. Esto es lo que ocurre en los aerogeneradores y en las turbinas de las centrales eléctricas

En el caso de un generador eléctrico, el resultado es una d.d.p. que tiene signo contrario a la corriente, de forma que el flujo de trabajo eléctrico es negativo, es decir, está saliendo del sistema, no entrando.

Efecto Joule

En el caso particular de un cable (o, en general, de un resistor caracterizado por una resistencia $R$), si el extremo A está a mayor voltaje que B, la corriente va de A a B. El flujo de trabajo eléctrico (o potencia eléctrica) que entra en la resistencia es

$P_{\mathrm {e} }={\dot {W}}_{\mathrm {in} }=I\,\Delta V=I(V_{A}-V_{B})$

Por la ley de Ohm para una resistencia, podemos escribir esta potencia de varias formas alternativas

$\Delta V=IR\qquad \Rightarrow \qquad P_{\mathrm {e} }={\dot {W}}_{\mathrm {in} }=I\,\Delta V=I^{2}R={\frac {(\Delta V)^{2}}{R}}$

esta es la llamada ley de Joule (o efecto Joule). En una resistencia eléctrica se consume trabajo eléctrico. De acuerdo con el primer principio de la termodinámica tendremos que

${\dot {W}}_{\mathrm {in} }={\frac {\mathrm {d} E}{\mathrm {d} t}}+{\dot {Q}}_{\mathrm {out} }$

es decir, la potencia eléctrica que metemos, en parte se emplea en aumentar la energía almacenada (que puede ser en forma de energía interna, lo que vemos como un aumento de temperatura del sistema, pero también en otros tipos de energía) y parte se escapa al exterior en forma de calor. Es decir, un cable por el cual circula una corriente aumenta su temperatura y radia calor al exterior. Esta disipación a veces es deseada, como en el caso de una estufa, pero normalmente es indeseable y hay que procurar reducirla (puede demostrarse que debido a la corriente existe una producción de entropía que hay que reducir para mejorar la eficiencia de un sistema).

  

La cantidad total de energía eléctrica consumida es la integral de la potencia

$W_{\mathrm {in} }=\int _{0}^{t}P_{\mathrm {in} }\,\mathrm {d} t=\int _{0}^{t}I^{2}R\,\mathrm {d} t$

En el caso de una corriente continua ($I=\mathrm {cte}$) el resultado de la integral es una simple multiplicación. Para una corriente variable (como la corriente alterna, por ejemplo), habrá que hacer el cálculo correspondiente.

Almacenamiento de energía eléctrica

No siempre la potencia eléctrica que entra se escapa en forma de trabajo o calor. También puede almacenarse en el interior del sistema en forma de energía electrostática.

Condensador ideal

Imaginemos que nuestro sistema es un condensador ideal (sin conductancia) en el cual la corriente que llega se emplea en variar la carga almacenada en el condensador

$I={\frac {\mathrm {d} Q}{\mathrm {d} t}}$

mientras que la diferencia de potencial entre las placas es proporcional a la carga almacenada

$Q=C(V_{A}-V_{B})\,$

Esto da, para la potencia

${\dot {W}}_{\mathrm {in} }=(V_{A}-V_{B})I=\Delta V\,{\frac {\mathrm {d} \ }{\mathrm {d} t}}(C\Delta V)={\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {1}{2}}C(\Delta V)^{2}\right)$

es decir, el trabajo que entra en la unidad de tiempo es igual a lo que aumenta la energía almacenada en el condensador.

También funciona a la inversa. Si el condensador se está descargado resulta una corriente en sentido contrario y la disminución de la energía almacenada es igual al trabajo que sale del sistema por segundo.

Condensador real

Si tenemos un condensador con pérdidas, la corriente que llega a él se compone de una parte capacitiva y de una parte resistiva

$I={\frac {\mathrm {d} Q}{\mathrm {d} t}}+\int {\vec {J}}\cdot \mathrm {d} {\vec {S}}$

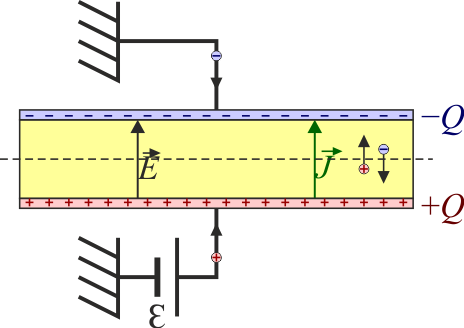
Ambos términos se pueden poner en función de la diferencia de potencial entre placas

$Q=C\,\Delta V\qquad \qquad \int {\vec {J}}\cdot \mathrm {d} S={\frac {\Delta V}{R}}$

lo que da, para la corriente que llega por el cable

$I=C{\frac {\mathrm {d} \ }{\mathrm {d} t}}(\Delta V)+{\frac {\Delta V}{R}}$

y para el flujo de trabajo eléctrico

${\dot {W}}_{\mathrm {in} }=I\,\Delta V=\Delta V{\frac {\mathrm {d} \ }{\mathrm {d} t}}(C\,\Delta V)+{\frac {(\Delta V)^{2}}{R}}$

que se puede escribir en la forma

${\dot {W}}_{\mathrm {in} }={\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {1}{2}}C(\Delta V)^{2}\right)+{\frac {(\Delta V)^{2}}{R}}$

es decir, que el trabajo que entra parte se va en aumentar la energía almacenada y parte se va en potencia disipada. Esta fórmula contine tres casos particulares de interés.

• Si la corriente es continua, la energía almacenada es constante, el primer sumando se anula y todo el trabajo que entra se disipa por efecto Joule.
• Si el condensador es ideal, no hay disipación de energía por efecto Joule y todo el trabajo que entra se almacena en el condensador
• Si el sistema está aislado, no hay flujo de trabajo desde el exterior y la energía almacenada en el condensador se disipa por efecto Joule.

${\dot {W}}_{\mathrm {in} }=0\qquad \Rightarrow \qquad -{\frac {\mathrm {d} \ }{\mathrm {d} t}}\left({\frac {1}{2}}C(\Delta V)^{2}\right)={\frac {(\Delta V)^{2}}{R}}$