Posicionamiento de un cohete en órbita, Enero 2023 (G.I.C.)

Enunciado

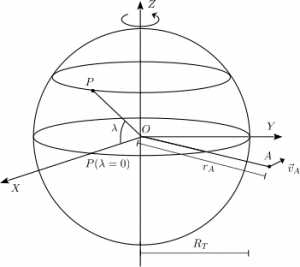
Las agencias espaciales intentan lanzar los cohetes lo mas cerca posible del Ecuador para aprovechar la rotación de la Tierra. Vamos a examinar la razón de esto y cuanto es la ganancia de energía cinética al lanzar los cohetes lo mas cerca posible del Ecuador. El dibujo representa la Tierra. El punto $P$, situado en su superficie, tiene una latitud $\lambda$. El punto $A$ está situado en el plano del Ecuador a una distancia $r_{A}$ del centro de la Tierra. El sistema de ejes $OXYZ$ está fijo en el espacio, de modo que la Tierra rota respecto a él en el sentido en que se indica en la figura.

Dato $R_{T}=6400\,\mathrm {km}$.

1. A partir de la Ley de Gravitación Universal de Newton, encuentra la velocidad que debe tener un satélite situado en el punto $A$ para que orbite alrededor de la Tierra.
2. Si el punto $P$ de la superficie de la Tierra tiene una latitud $\lambda$, encuentra su rapidez, $v_{P}$, debida a la rotación de la Tierra.
3. Supongamos que el punto $P$ se sitúa sobre el Ecuador ($\lambda =0$), y que un cohete se lanza con rapidez $v_{c}$ respecto a la superficie de la Tierra y palelamente a la superficie de esta. Usando la conservación de energía mecánica cuanto debe valer $v_{c}$ para que el cohete puede ponerse en órbita en el punto $A$ (se desprecia el efecto de la atmósfera)
4. Encuentra el valor numérico de $v_{C}$ si el punto $A$ se sitúa a una distancia infinita de la Tierra. Para ello tienes que expresar el producto $GM_{T}$ en función de $g$, la aceleración de la gravedad en su superficie (siendo $G$ la constante de gravitación universal y $M_{T}$ la masa de la Tierra).

Solución

Velocidad orbital

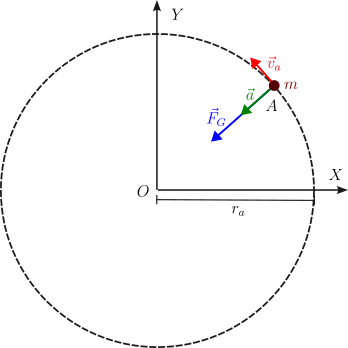
La figura de la derecha muestra la fuerza gravitatoria, la aceleración y la velocidad de una partícula que se encuentre en órbita alrededor de la Tierra a una distancia $r_{a}$ de su centro. La fuerza gravitatoria es

$|{\vec {F}}_{G}|={\dfrac {GM_{T}m}{r_{a}^{2}}},$

donde $m$ es la masa de la partícula, $G$ es la constante de gravitación universal y $M_{T}$ es la masa de la Tierra. La fuerza ${\vec {F}}_{G}$ es la única que actúa sobre la masa $m$. Aplicando la Segunda Ley de Newton, tenemos

$m|{\vec {a}}|=|{\vec {F}}_{G}|\Longrightarrow |{\vec {a}}|={\dfrac {GM_{T}}{r_{a}^{2}}}.$

Por otro lado, si la partícula está en órbita estacionaria, está describiendo un movimiento circular uniforme. Entonces, su aceleración sólo tiene componente normal y vale

$|{\vec {a}}|=a_{N}={\dfrac {v_{a}^{2}}{r_{a}}}.$

Igualando las dos expresiones para la aceleración encontramos la velocidad orbital

$v_{a}={\sqrt {GM_{T}/r_{a}}}.$

Rapidez del punto P

Un punto en la superficie describe un movimiento circular con velocidad angular $\omega _{0}$. El radio de la circunferencia que describe es

$r_{P}=R_{T}\cos \lambda .$

La velocidad angular del movimiento circular que describe la partícula es

$\omega _{0}={\dfrac {2\pi }{T}}$

siendo $T$ igual a 1 dia. El valor numérico es

$\omega _{0}={\dfrac {2\pi }{1\,\mathrm {dia} }}\times {\dfrac {1\,\mathrm {dia} }{24\,\mathrm {h} }}\times {\dfrac {1\,\mathrm {hora} }{3600\,\mathrm {s} }}=7.27\times 10^{-5}\,\mathrm {rad/s}$

Entonces, su rapidez es

$v_{P}=\omega _{0}r_{P}=\omega _{0}R_{T}\cos \lambda .$

Para un punto en el Ecuador, con $\lambda =0$, es

$v_{P}^{\,Ec}=\omega _{0}R_{T}=465\,\mathrm {m/s} .$

Lanzamiento desde un punto del Ecuador

Si el cohete se lanza desde un punto del Ecuador, su energía potencial es

$U_{P}=-{\dfrac {GmM_{T}}{R_{T}}}.$

Como vimos en clase, en está fórmula se asume que la energía potencial gravitatoria es nula infinitamente lejos de la Tierra.

Cuando está en la superficie de la Tierra, el cohete tiene una energía cinética debido a que se mueve con su superficie. El problema dice que despega siguiendo una trayectoria paralela al suelo. Entonces, su rapidez total es la suma de la rapidez asociada a la rotación y de la velocidad respecto a la superficie, $v_{c}$. Esta energía cinética vale

$T_{P}={\dfrac {1}{2}}m(v_{P}^{\,Ec}+v_{c})^{2}$

La energía mecánica del cohete en el momento del lanzamiento es

$E_{P}=T_{P}+U_{P}={\dfrac {1}{2}}m(v_{P}^{\,Ec}+v_{c})^{2}-{\dfrac {GmM_{T}}{R_{T}}}.$

Para que el cohete está en órbita en el punto $A$, su rapidez debe ser la calculada en el apartado 1. Entonces, la energía mecánica en $A$ debe ser

$E_{A}={\dfrac {1}{2}}{\dfrac {GmM_{T}}{r_{A}}}-{\dfrac {GmM_{T}}{r_{a}}}=-{\dfrac {1}{2}}{\dfrac {GmM_{T}}{r_{A}}}.$

Al despreciar el efecto del aire, la energía mecánica debe conservarse, por lo que, igualando las dos expresiones obtenemos la rapidez de despegue

$v_{c}={\sqrt {\dfrac {2GM_{T}}{R_{T}}}}{\sqrt {1-{\dfrac {R_{T}}{2r_{a}}}}}-v_{P}^{\,Ec}.$

Valor numérico si A está en el infinito

Si hacemos $r_{A}\to \infty$, el valor de la rapidez del cohete respecto al suelo es

$v_{c}^{\,\infty }={\sqrt {\dfrac {2GM_{T}}{R_{T}}}}-v_{P}^{\,Ec}.$

Para obtener el valor numérico, observamos que el peso de una masa en la superficie de la Tierra es

$\left.{\begin{array}{l}P=mg\\P=m{\dfrac {GM_{T}}{R_{T}^{2}}}\end{array}}\right|\Longrightarrow {\dfrac {GM_{T}}{R_{T}}}=gR_{T}.$

Entonces, la velocidad del cohete puede expresarse como

$v_{c}^{\,\infty }={\sqrt {2gR_{T}}}-v_{P}^{\,Ec}=10.7\,\mathrm {km/s} .$