Particula con un muelle horizontal y otro inclinado, Noviembre 2013 (G.I.C.)
Enunciado
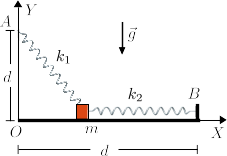
Un partícula de masa reposa sobre un plano horizontal sin rozamiento. Está atada a dos muelles de constantes elásticas y y longitud natural nula, anclados en los puntos y . La partícula no puede desplazarse a lo largo del eje .
- Dibuja el diagrama de cuerpo libre de la partícula.
- Condición para que la masa no se separe del plano.
- Posición de equilibrio de la partícula en la situación del apartado anterior.
- Supongamos que existe rozamiento entre la partícula y el plano, con un coeficiente de rozamiento estático . Si es la coordenada de la partícula sobre el eje , en situación de equilibrio, calcula el módulo de la fuerza de rozamiento.
Solución
Diagrama de cuerpo libre
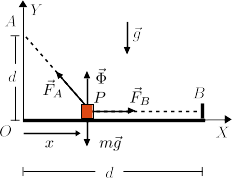
En este apartado el contacto es liso, por lo que no hay fuerza de rozamiento. Las fuerzas que actúan sobre la partícula son las dos de los muelles, su peso y la fuerza de reacción vincular. La fuerza de reacción vincular hay que incluirla siempre, aunque luego su valor sea cero.
La imagen de la derecha muestra la dirección de las fuerzas. En el sistema de ejes indicado las fuerzas se expresan
Hemos usado que los muelles tiene longitud natural nula.
Análisis del equilibrio mecánico
Aplicamos la condición de equilibrio mecánico de una partícula a las fuerzas que actúan sobre ella
En este caso las componentes en el eje no cuentan. Tenemos entonces 2 ecuaciones escalares
La fuerza de reacción vincular aparece para que la masa no atraviese el plano. Ésta se separara del plano cuando la fuerza de reacción vincular sea cero. La condición para que esto no ocurre es
La posición de equilibrio es
Podemos ver que el resultado es razonable. Si ( el muelle 1 es mucho mas fuerte que el 2) . Por otro lado, si tenemos .
Análisis con rozamiento
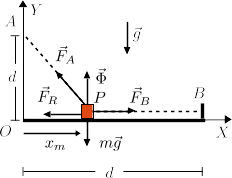
El rozamiento introduce una fuerza mas, tangente al plano. En la figura la hemos puesto apuntando hacia la izquierda, pero no conocemos su sentido a priori, sólo su dirección.
puede ser positivo o negativo. Si es positivo la fuerza apunta hacia la derecha. Si es negativo apunta hacia la izquierda (correspondería al caso de la figura).
Al aplicar la condición de equilibrio mecánico tenemos ahora
y obtenemos dos ecuaciones escalares, una por cada componente
Ahora tenemos tres incógnitas, , y , y sólo dos ecuaciones. De la segunda podemos despejar , pero no nos quedan todavía dos incógnitas con una ecuación. ¿Qué pasa aquí? La respuesta es que ahora no tenemos una posición de equilibrio, sino un rango de ellas. Para cada valor de , la fuerza de rozamiento se ajusta para que la partícula no se mueva. Así, si la coordenada de la partícula es , la primera ecuación nos da el valor de la fuerza de rozamiento
Puede apuntar hacia la derecha o hacia la izquierda . Es interesante señalar que no aparece el coeficiente de rozamiento.
Rango de posiciones de equilibrio (no preguntado en el examen)
Ya hemos respondido lo que nos pedían, pero podemos ir un poco mas allá. Dado un valor la fuerza de rozamiento se ajusta para que la partícula no se mueva. Pero la fuerza de rozamiento tiene un módulo máximo, es decir, hay valores de para los que la fuerza de rozamiento no puede asegurar el equilibrio, y la partícula se mueve. Los valores máximo y mínimo de dan el rango de posiciones de equilibrio.
La condición para que la fuerza de rozamiento sea capaz de asegurar el equilibrio es
Para un valor dado de , el valor de la fuerza de rozamiento es
Tenemos dos sumandos de signos contrarios. Si el primero es mayor que el segundo el módulo es
Mientras que si el primero es menor que el segundo el módulo es
Por otro lado, para que la masa esté siempre en contacto con el suelo debe cumplirse
y por tanto el módulo de la fuerza de reacción vincular es siempre
Usando la primera expresión del módulo de tenemos
Usando la otra expresión del módulo de obtenemos una condición de mínimo de la posición
Es decir, el rango de posiciones de equilibrio es
Es interesante observar que el rango de posiciones de equilibrio aparece alrededor de la posición de equilibrio sin rozamiento. En efecto tenemos que
Nos podríamos hacer otra pregunta. ¿Qué condiciones se tienen que cumplir para que todos los valores de en el intervalo sean posiciones de equilibrio? Intenta encontrar la respuesta.





































![{\displaystyle [0,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a68607f44d0d66b19df7ed5b7d0e6e41e314b37)