Partícula sobre una rampa con muelle

Enunciado

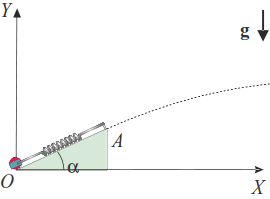
Para lanzar una partícula material de masa $m$ se dispone de una rampa de lanzamiento de longitud $l$ y un resorte de constante recuperadora $k$ y longitud natural nula que tiene el extremo fijado al punto $A$ de la rampa. Para proceder al lanzamiento, la partícula se coloca en el otro extremo del resorte, situado en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O} .

1. Determina las condiciones iniciales de posición y velocidad para el movimiento libre de la partícula (cuando la partícula abandona la rampa en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A} ), en función del ángulo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha} que forma la rampa con la horizontal, en las siguientes situaciones
   1. El rozamiento de la partícula en la rampa es despreciable.
   2. El rozamiento seco de la partícula en la rampa está caracterizado por un coeficiente dinámico Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mu} .
2. Calcula la altura máxima de la partícula respecto del suelo en las dos situaciones del apartado anterior.

Solución

Rozamiento nulo

Condiciones en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A }

La partícula se mueve sobre la rampa impulsada por el resorte y bajo la acción de la gravedad. Se trata de dos fuerzas conservativas, por lo que podemos aplicar la conservación de la energía mecánica. Escogemos como origen de energía potencial la altura del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } . Cuando la partícula está en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } se encuentra en reposo, por lo que su energía mecánica es se debe a la energía potencial del muelle.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_O = \dfrac{1}{2}\,k\,l^2 }

Cuando llega al punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } la energía potencial del muelle es cero, el módulo de su velocidad es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_A } y la altura sobre el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h = l\,\mathrm{sen}\,\alpha } . La energía mecánica en Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_A = \dfrac{1}{2}\,m\,v_A^2 + m\,g\,l\,\mathrm{sen}\,\alpha }

Igualando las dos energías obtenemos el módulo de la velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_A = \sqrt{ \dfrac{k\,l^2}{m} - 2\,g\,l\,\mathrm{sen}\,\alpha} }

El vector de posición del punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } , tomando como origen el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } , es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_A = l\cos\alpha\,\vec{\imath} + l\,\mathrm{sen}\,\alpha\,\vec{\jmath} }

En el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } el vector velocidad es tangente a la rampa. Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_A = v_A\cos\alpha\,\vec{\imath} + v_A\,\mathrm{sen}\,\alpha\,\vec{\jmath} }

donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_A } es la expresión obtenida anteriormente.

Comentarios sobre la expresión de la velocidad

El módulo de la velocidad no puede ser un número complejo. Para que la solución obtenida tenga sentido el radicando debe ser positivo. Es decir

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{k\,l^2}{m} \geq 2\,g\,l\,\mathrm{sen}\,\alpha \Longrightarrow \dfrac{k\,l^2}{2} \geq m\,g\,l\,\mathrm{sen}\,\alpha = m\,g\,h_A }

Esta expresión significa que la energía elástica del muelle cuando está estirado debe ser mayor que la variación de energía potencial gravitatoria entre el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } y el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } . Si esto no ocurre, la partícula se para antes de llegar a lo alto de la rampa.

Altura máxima

Tras abandonar la rampa, la única fuerza que actúa sobre la partícula es la de la gravedad. El movimiento que describe es el de un tiro parabólico. La altura máxima se alcanza cuando la componente vertical de la velocidad se hace cero (punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P } ). Como la componente horizontal es constante, ya que no hay fuerza actuando en la dirección horizontal, en el instante en que la partícula alcanza su punto más alto su energía cinética es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle K_{max} = \dfrac{1}{2}\,m\,v_{Ax}^2 = \dfrac{1}{2}\,m\,v_A^2\cos^2\alpha }

También en ese instante la energía potencial gravitatoria respecto al suelo es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle U_g^{max} = m\,g\,h_{max} }

La energía mecánica en este punto debe ser igual a la que tenía la partícula en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } . Además, en este caso en el que no hay rozamiento, es igual a la energía mecánica de la partícula en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } . Por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_P = E_A \Longrightarrow \dfrac{1}{2}\,m\,v_A^2\cos^2\alpha + m\,g\,h_{max} = \dfrac{1}{2}\,m\,v_A^2 + m\,g\,l\,\mathrm{sen}\,\alpha }

Despejando obtenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h_{max} = l\,\mathrm{sen}\,\alpha + \dfrac{v_A^2\,\mathrm{sen}^2\alpha}{2g} }

Con rozamiento

Condiciones en el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A }

El planteamiento del problema es similar. La única diferencia es que la energía mecánica no se conserva en el movimiento de la partícula sobre la rampa. Hay que tener en cuenta el trabajo realizado por la fuerza de rozamiento. Tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle E_A = E_O + W_{roz} }

Al ser un rozamiento dinámico, el módulo de la fuerza de rozamiento es proporcional a la fuerza normal que el plano ejerce sobre la partícula. La fuerza de rozamiento es constante y opuesta a la velocidad de la partícula sobre la rampa. Tenemos por tanto

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle |\vec{F}_{roz}| = \mu\,N = \mu\,m\,g\cos\alpha. }

El trabajo de rozamiento en el desplazamiento de la partícula desde el punto Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle O } hasta el Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle A } es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle W_{roz} = \int\limits_O^A\vec{F}_{roz}\cdot\mathrm{d}\vec{r} = -\int\limits_O^A|\vec{F}_{roz}|\,\mathrm{d}r = -|\vec{F}_{roz}|\,\int\limits_O^A\mathrm{d}r = -|\vec{F}_{roz}|\,l =-\mu\,m\,g\,l\,\cos\alpha }

Obtenemos el módulo de la velocidad del balance de energías

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{1}{2}\,m\,v_{Ar}^2 + m\,g\,l\,\mathrm{sen}\,\alpha = \dfrac{1}{2}\,k\,l^2 - \mu\,m\,g\,l\,\cos\alpha }

Despejando tenemos

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_{Ar} = \sqrt{\dfrac{k\,l^2}{m} - 2\,g\,l\,(\mathrm{sen}\,\alpha +\mu\cos\alpha)} }

Las condiciones iniciales son iguales que en el caso sin rozamiento sustituyendo el valor del módulo de la velocidad por el obtenido aquí

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{l} \vec{r}_A = l\cos\alpha\,\vec{\imath} + l\,\mathrm{sen}\,\alpha\,\vec{\jmath} \\ \\ \vec{v}_{Ar} = v_{Ar}\cos\alpha\,\vec{\imath} + v_{Ar}\,\mathrm{sen}\,\alpha\,\vec{\jmath} \\ \\ \end{array} }

Altura máxima

El razonamiento es el mismo que en el apartado con rozamiento. El resultado es igual cambiando el módulo de la velocidad por el obtenido aquí. La altura máxima es

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle h_{max} = l\,\mathrm{sen}\,\alpha + \dfrac{v_{Ar}^2\,\mathrm{sen}^2\alpha}{2g} }