Enunciado
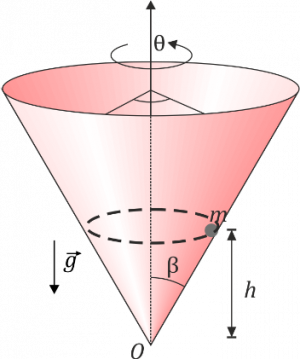
Una partícula está obligada a moverse por la superficie interior de un cono que tiene su vértice en el origen y que tiene un semiángulo de apertura β, es decir, la superficie del cono es, en cilíndricas Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle z=\rho/\tan(\beta)}
. La partícula se mueve sin rozamiento por esta superficie y se halla sometida a la acción de la gravedad, que va en la dirección y sentido del eje OZ negativo
- Obtenga las ecuaciones de movimiento para esta partícula, empleando como coordenadas las cilíndricas, introduciendo las fuerzas de reacción oportunas.
- Reduzca este sistema a dos ecuaciones, una para la distancia al vértice, Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r=\sqrt{\rho^2+z^2}}
y otra para el ángulo θ, de manera que no aparezcan ρ, z ni la reacción.
- ¿A qué velocidad debe moverse la partícula si se desea que describa un movimiento circular horizontal, a una altura H respecto al vértice? ¿Cuánto vale la fuerza de reacción en ese caso?
- Supongamos que parte de una altura H con una velocidad horizontal menor que la del apartado anterior. ¿Cuánto vale la mínima altura a la que llega la partícula?
Ecuaciones de movimiento
En forma vectorial, la segunda ley de Newton queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m\vec{a}=\vec{F}_n+m\vec{g}}
siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \vec{F}_n}
la fuerza normal al cono. Esta fuerza posee una componente Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_n\cos(\beta)}
en la dirección radial y una Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_n\mathrm{sen}(\beta)}
en la dirección vertical hacia arriba.
Si escribimos esta ecuación en coordenadas cilíndricas, tenemos, separando por componentes
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\begin{array}{rcrcl}\rho:&\qquad &m\left(\ddot{\rho}-\rho\dot{\theta}^2\right)&=&-F_nS\\ \theta:&\qquad& m(2\dot{\rho}\dot{\theta}+\rho\ddot{\theta})&=&0\\ z:&\qquad&m\ddot{z}&=&F_nS-mg\end{array}\right.}
donde Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle S =\mathrm{sen}(\beta)}
y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle C = \cos(\beta)}
, que en este problema son dos constantes.
Obsérvese que en la ecuación en la componente θ el segundo miembro es nulo, ya que ni la fuerza normal ni el peso tienen componente en esta dirección.
En estas ecuaciones ρ y z no son independientes, sino que están relacionados por la ecuación de vínculo
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{\rho}{z}= an{}(\beta)\qquad\Rightarrow\qquad -Sz+C\rho = 0}
Reducción de las ecuaciones
En las ecuaciones anteriores puede, con ayuda de la ecuación de vínculo, llegarse a ecuaciones separadas para ρ y z, pero es más sencillo hacer un cambio de variable como el sugerido aquí.
Introduciendo la distancia al vértice queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \rho = rS\qquad\qquad z = rC}
y, si sustituimos en las ecuaciones de movimiento
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \left\{\begin{array}{rcrcl}\rho:&\qquad &m\left(\ddot{r}S-rS\dot{\theta}^2\right)&=&-F_nC\\ \theta:&\qquad& m(2\dot{r}\dot{\theta}S+rS\ddot{\theta})&=&0\\ z:&\qquad&m\ddot{r}C&=&F_nS-mg\end{array}\right.}
Eliminamos la rearcción normal al cono multiplicando la primera por el seno, la segunda por el coseno y sumando. Queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle m(\ddot{r}(S^2+C^2)-rS^2\dot{\theta}^2)=-mgC \qquad\Rightarrow\qquad \ddot{r}-rS^2\dot{\theta}^2=-gC}
que, junto con la segunda simplificada
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 2\dot{r}\dot{\theta}+r\ddot{\theta}=0}
es el sistema de ecuaciones buscado.
Circunferencias horizontales
Para que haya circunferencias horizontales, la distancia r debe ser una constante, de valor
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r = \frac{H}{C}\qquad\qquad\dot{r}=0\qquad\qquad \ddot{r}=0}
Llevando esto a las ecuaciones de movimiento queda
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle 0 - \frac{H}{C}S^2\dot{\theta}^2 = -gC\qquad\qquad 0+\frac{H}{C}\ddot{\theta}=0 }
De la segunda se deduce, integrando, que
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}=\Omega=\mathrm{cte}}
y, sustituyendo en la primera ecuación
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -\frac{H}{C}S^2\Omega^2 = -gC\qquad\Rightarrow\qquad \Omega = \sqrt{\frac{g}{H}}\,\frac{C}{S}}
Esta es la velocidad angular con la que debe dar vueltas. la velocidad lineal es esta, multiplicada por el radio
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle v_c=\Omega\rho =\Omega H\, an{}(\beta)=\sqrt{gH}}
Es llamativo que la velocidad no dependa de la apertura del cono.
Se puede llegar a este resultado simplemente aplicando que en este caso el peso y la reacción producen una aceleración puramente normal
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle -m\frac{v_c^2}{R}\vec{u}_\rho=-F_nC\vec{u}_\rho+(F_nS-mg)\vec{k}}
de donde
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle F_n = \frac{mg}{S} \qquad\qquad v_c^2 =\frac{F_nCR}{m}=\frac{gRC}{S}=gH\qquad\Rightarrow\qquad v_c=\sqrt{gH}}
Mínima distancia al vértice
Este apartado es bastante más complicado que los anteriores y requiere el uso de constantes de movimiento.
Partimos del sistema de ecuaciones de movimiento
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \begin{array}{rcl}\ddot{r}-rS^2\ddot{\theta}^2&=&-gC\\ 2\dot{r}\dot{\theta}+r\ddot{\theta}=0\end{array}}
De estas dos ecuaciones se deduce la conservación de la energía mecánica
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{2}m(\dot{r}^2+r^2S^2\dot{\theta}^2)+mgrC = E}
y de la cantidad, relacionada con el momento cinético,
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2\dot{\theta}=\ell}
Se puede comprobar derivando cada una de estas cantidades respecto al tiempo y sustituyendo las ecuaciones de movimiento.
Los valores de estas cantidades los sacamos de las condiciones iniciales
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r = \frac{H}{C} \qquad \dot{r}=0\qquad\dot{\theta}=\frac{v_0}{R}=\frac{v_0C}{HS}}
de donde
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{2}(\dot{r}^2+r^2S^2\dot{\theta}^2)+grC=\frac{1}{2}v_0^2 + gH}
y
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2\dot{\theta}=\frac{Hv_0}{CS}}
Los puntos de máxima y mínima distancia cumplen que r es un máximo o mínimo, es decir, que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{r}=0}
. Para estos puntos
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{2}(r^2S^2\dot{\theta}^2)+grC=\frac{1}{2}v_0^2 + gH}
y
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2\dot{\theta}=\frac{Hv_0}{CS}}
Despejamos de la segunda Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \dot{\theta}}
y sustituimos en la primera
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{2}\left(\frac{H^2v_0^2}{C^2r^2}\right)+grC=\frac{1}{2}v_0^2 + gH}
Multiplicamos por Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^2}
y resulta una ecuación de tercer grado
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r^3 (gC)-\left(\frac{1}{2}v_0^2 + gH\right)r^2 + \frac{H^2v_0^2}{2C^2} = 0}
La solución de una ecuación de tercer grado es normalmente muy complejo, pero en este caso conocemos una solución, ya que la partícula parte de r máximo, luego
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://wikimedia.org/api/rest_v1/»:): {\displaystyle r_\mathrm{max}=\frac{H}{C}}
Esto permite simplificar la cúbica mediante Ruffini. Queda una ecuación de segundo grado una de cuyas raíces es la distancia mínima buscada. La otra tiene un valor negativo, que no tiene sentido en este caso.
