Péndulo con velocidad inicial, Enero 2014 (G.I.C.)

Enunciado

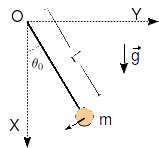
Una masa $m$ cuelga de un hilo inextensible sin masa. En la posición inicial el hilo forma un ángulo $\theta _{0}$ con la vertical. La masa empieza a moverse con velocidad de módulo $v_{0}$ y con la dirección y sentido indicados en la figura.

1. ¿Cuál es la expresión de la velocidad en función del ángulo?
2. Con los valores numéricos $L=10.0\,\mathrm {cm}$, $\theta _{0}=\pi /6$, ¿qué condición debe cumplir $v_{0}$ para que la masa de una vuelta completa?

Solución

Las fuerzas que actúan sobre la masa durante su movimiento son el peso y la tensión de la cuerda. La fuerza ejercida por la cuerda es siempre perpendicular al movimiento (éste es circular), por lo que no realiza trabajo. Como sólo la fuerza conservativa realiza trabajo, la energía mecánica se conserva.

Escogemos $x=0$ como origen de energía potencial gravitatoria. En el instante inicial la energía potencial es

$U_{g}(\theta _{0})=-mgL\cos \theta _{0}$

y la energía cinética es

$T(\theta _{0})={\dfrac {1}{2}}mv_{0}^{2}$

Por tanto, la energía mecánica en todo instante es

$E=T(\theta _{0})+U_{g}(\theta _{0})={\dfrac {1}{2}}mv_{0}^{2}-mgL\cos \theta _{0}$

Para un ángulo $\theta$ cualquiera la energía potencial gravitatoria es

$U_{g}(\theta )=-mgL\cos \theta$

y la energía cinética es

$T(\theta )={\dfrac {1}{2}}mv^{2}(\theta )$

La energía mecánica para un ángulo $\theta$ arbitrario es

$E(\theta )={\dfrac {1}{2}}mv^{2}(\theta )-mgL\cos \theta$

Esta energía debe ser igual a la inicial. Igualando las dos expresiones y despejando la velocidad obtenemos

$v(\theta )={\sqrt {v_{0}^{2}-2gL\,(\cos \theta _{0}-\cos \theta )}}$

Para que de una vuelta completa la condición es que cuando la masa esté en el punto mas alto $(\theta =-\pi )$ la velocidad sea cero. Es decir

$v(-\pi )=0\to v_{0}^{min}={\sqrt {2gL(\cos \theta _{0}+1)}}$