Péndulo cónico, Enero 2018 (G.I.E.R.M.)

Enunciado

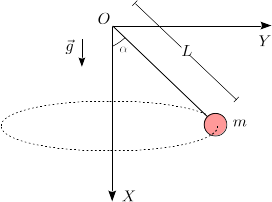
Una masa $m$ cuelga de un hilo tenso, inextensible y sin masa, de longitud $L$. La masa se mueve de modo que describe un movimiento circular uniforme en torno al eje $X$, como se indica en la figura. La masa está también sometida a la acción de la gravedad. En el instante mostrado en la figura la partícula está en el plano $OXY$.

1. Dibuja el diagrama de cuerpo libre de la masa. Añade a este diagrama el vector aceleración de la partícula. ¿Cuanto vale el radio de la circunferencia que describe la partícula?
2. Aplicando la Segunda Ley de Newton, determina la relación entre la rapidez de la partícula y el ángulo $\alpha$ que forma el hilo con la vertical.
3. Suponiendo que $\alpha =\pi /4$, y que la dirección de la velocidad apunta en el sentido negativo del eje $Z$, calcula el momento angular de la partícula respecto al punto $O$ en el instante que se muestra en la figura, así como su derivada temporal.

Solución

Diagrama de cuerpo libre

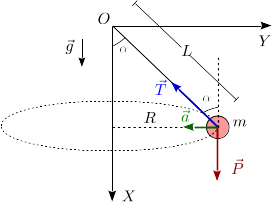
Sobre la partícula una fuerza activa, el peso, y una fuerza vincular, la tensión de la cuerda. La fuerza que la cuerda ejerce sobre la partícula está dirigida en la dirección de la propia cuerda, como se ve en la figura.

La partícula realiza un movimiento circular uniforme. Esto no quiere decir que la aceleración sea cero, sino que la aceleración tiene sólo componente normal. Además, tiene que apuntar hacia el eje $X$ en todo instante, pues la aceleración siempre apunta hacia la parte cóncava de la trayectoria. Además, el módulo de la aceleración es

$|{\vec {a}}|={\dfrac {v^{2}}{R}},$

donde $v$ es la rapidez de la partícula y $R$ es el radio de la circunferencia que describe. Por trigonometría obtenemos

$R=L\,\mathrm {sen} \,\alpha .$

Ángulo

La Segunda Ley de Newton en este caso es

$m{\vec {a}}={\vec {P}}+{\vec {T}}.$

En el sistema de ejes de la figura las fuerzas aplicadas sobre la partícula se expresan como sigue

${\begin{array}{l}{\vec {P}}=mg\,{\vec {\imath }},\\\\{\vec {T}}=-T\cos \alpha \,{\vec {\imath }}-T\,\mathrm {sen} \,\alpha \,{\vec {\jmath }}.\end{array}}$

El término de inercia es

$m{\vec {a}}=-m{\dfrac {v^{2}}{R}}\,{\vec {\jmath }}.$

Entonces la Segunda Ley nos da dos ecuaciones

${\begin{array}{lcl}X)&\to &mg-T\cos \alpha =0,\\&&\\Y)&\to &-m{\dfrac {v^{2}}{R}}=-T\,\mathrm {sen} \,\alpha .\end{array}}$

Despejando la tensión en la primera ecuación y despejando en la segunda obtenemos la relación pedida

$v^{2}=gR\tan \alpha =gL\,\mathrm {sen} \,\alpha \tan \alpha .$

La fuerza que ejerce la cuerda es

${\vec {T}}=-mg\,{\vec {\imath }}-mg\tan \alpha \,{\vec {\jmath }}.$

La componente en $X$ compensa al peso mientras que la componente en $Y$ es la que hace girar a la partícula.

Hay dos valores límites interesantes para el ángulo $\alpha$. Si $\alpha =0$ tenemos $v=0$. En esta situación la partícula no se mueve y la fuerza que ejerce la cuerda compensa exactamente al peso.

Si $\alpha \to \pi /2$, tenemos $v\to \infty$. Es decir, cuanto mayor sea la rapidez de la partícula, más horizontal se pone la cuerda. Para que esta sea completamente horizontal la rapidez de la partícula tiene que ser infinita.

Momento cinético

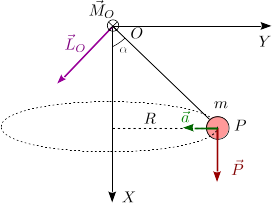
El momento cinético de la partícula respecto del punto $O$ es

${\vec {L}}_{O}={\overrightarrow {OP}}\times (m{\vec {v}})$

Por lo que dice el enunciado la velocidad en el instante indicado en la figura es

${\vec {v}}=-v_{0}\,{\vec {k}},$

con $v_{0}={\sqrt {gL\,\mathrm {sen} \,\alpha \tan \alpha }}={\sqrt {{\sqrt {2}}gL}}.$ El vector de posición es

${\overrightarrow {OP}}=L\cos \alpha \,{\vec {\imath }}+L\,\mathrm {sen} \,\alpha \,{\vec {\jmath }}={\dfrac {L}{\sqrt {2}}}\,{\vec {\imath }}+{\dfrac {L}{\sqrt {2}}}\,{\vec {\jmath }}.$

El momento cinético es

${\vec {L}}_{O}={\dfrac {mv_{0}L}{\sqrt {2}}}\,\left(-{\vec {\imath }}+{\vec {\jmath }}\right).$

No podemos derivar esta expresión respecto al tiempo pues sólo conocemos ${\vec {L}}_{O}$ en este instante. Pero podemos aplicar el Teorema del Momento Cinético

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}={\vec {M}}_{O}={\overrightarrow {OP}}\times {\vec {F}}_{T}$

siendo ${\vec {F}}_{T}$ la fuerza neta sobre la partícula. Tenemos

${\vec {M}}_{O}={\overrightarrow {OP}}\times ({\vec {P}}+{\vec {T}})={\overrightarrow {OP}}\times {\vec {P}}$

La tensión no crea momento pues es colineal con ${\overrightarrow {OP}}$. Entonces

${\dfrac {\mathrm {d} {\vec {L}}_{O}}{\mathrm {d} t}}=-{\dfrac {mgL}{\sqrt {2}}}\,{\vec {k}}.$