Oscilador armónico tridimensional

Enunciado

Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}=-\omega^2\vec{r}}

con Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \omega = 2.0\,\mathrm{rad}/\mathrm{s}} . Su posición inicial es Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_0=5\,\vec{\imath}\ (\mathrm{m})} .

1. Para el caso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0=\vec{0}\,\mathrm{m}/\mathrm{s}} . ¿Qué tipo de movimiento describe la partícula?
2. Para el caso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0=10.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}} , ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
3. Suponga ahora que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0=8.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}} , ¿cómo es ahora la trayectoria de la partícula?
4. Para los tres casos anteriores, determine

1. la rapidez,
2. las componentes intrínsecas de la aceleración,
3. los vectores tangente y normal,
4. el radio de curvatura y el centro de curvatura.

para los instantes Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0\,} , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t=0.25\pi\,\mathrm{s}} y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle t = 0.125\pi\,\mathrm{s}} .

Solución general

La solución general de la ecuación del oscilador armónico en 3D es de la forma

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}(t) = \vec{r}_0\cos(\omega t)+\frac{\vec{v}_0}{\omega}\mathrm{sen}(\omega t)}

siendo Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_0} la posición inicial y Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}_0} la velocidad inicial de la partícula.

En este problema tenemos para todos los casos, empleando las unidades fundamentales del SI,

$\omega =2\qquad \qquad {\vec {r}}_{0}=5{\vec {\imath }}\qquad \qquad {\vec {v}}_{0}=v_{0}{\vec {\jmath }}$

que al sustituir en la solución general nos dan la ecuación horaria

${\vec {r}}=5\cos(2t){\vec {\imath }}+{\frac {v_{0}}{2}}\mathrm {sen} (2t){\vec {\jmath }}$

A partir de esta ecuación horaria pueden hallarse todas las características del movimiento.

Caso v₀ = 0 m/s

El primer caso tiene velocidad inicial nula, lo que reduce la ecuación horaria a

${\vec {r}}=5\cos(2t){\vec {\imath }}$

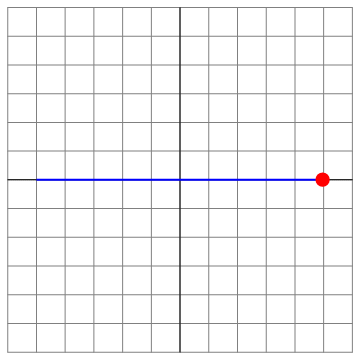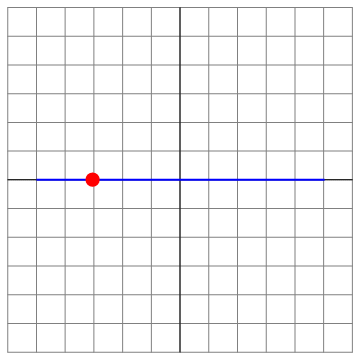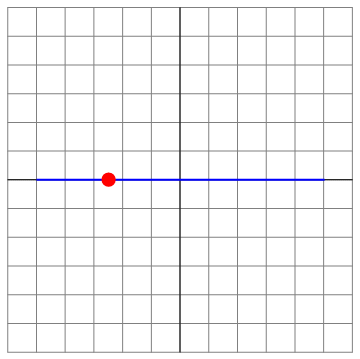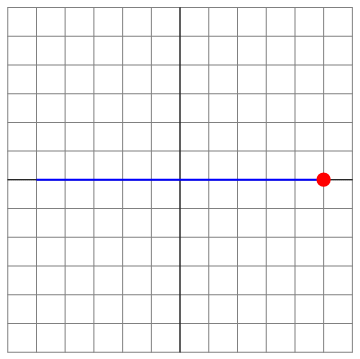
Esta es la ecuación de movimiento rectilíneo a lo largo del eje OX. Por cumplir la ecuación del oscilador armónico y ser rectilíneo, el movimiento es armónico simple.

Caso v₀ = 10 m/s

En el segundo caso, la ecuación horario se reduce a

${\vec {r}}=5\cos(2t){\vec {\imath }}+5\,\mathrm {sen} (2t){\vec {\jmath }}$

Este no es un movimiento rectilíneo. Sí es plano, porque tiene solo dos componentes, y verifica en todo momento que

$|{\vec {r}}|^{2}=x^{2}+y^{2}=5^{2}=\mathrm {cte}$

Por tanto se trata de un movimiento circular de radio 5 m alrededor del origen.

Además, podemos hallar la velocidad y rapidez del movimiento

${\vec {v}}=-10\,\mathrm {sen} (2t){\vec {\imath }}+10\cos(2t){\vec {\jmath }}\qquad \Rightarrow \qquad |{\vec {v}}|=10\,{\frac {\mathrm {m} }{\mathrm {s} }}$

Al ser la rapidez constante el movimiento es circular uniforme.

Caso v₀ = 8 m/s

El tercer caso tiene la ecuación horaria

${\vec {r}}=5\cos(2t){\vec {\imath }}+4\,\mathrm {sen} (2t){\vec {\jmath }}$

Esta trayectoria no es ni rectilínea ni circular. Si separamos en componentes nos queda

$x=5\cos(2t)\qquad \qquad y=4\,\mathrm {sen} (2t)\qquad \qquad z=0$

Podemos eliminar el tiempo de las dos primeras ecuaciones y combinarlas como

$\left({\frac {x}{5}}\right)^{2}+\left({\frac {y}{4}}\right)^{2}=1\qquad \qquad z=0$

que es la ecuación de una elipse de semiejes 5m y 4m

$v_{0}=0$	$v_{0}=10$	$v_{0}=8$

Cálculo de magnitudes

Rapidez

Para cualquier movimiento, la velocidad la da la derivada del vector de posición respecto al tiempo

${\vec {v}}=-10\,\mathrm {sen} (2t){\vec {\imath }}+v_{0}\cos(2t){\vec {\jmath }}$

Podemos comprobar que, como corresponde, la velocidad en t=0 coincide con la velocidad inicial.

La rapidez es el módulo de esta velocidad

$|{\vec {v}}|={\sqrt {10^{2}\mathrm {sen} ^{2}(2t)+v_{0}^{2}\cos ^{2}(2t)}}={\sqrt {100-(100-v_{0}^{2})\cos ^{2}(2t)}}$

• En el caso particular $v_{0}=0$ esta expresión se reduce a

$|{\vec {v}}|=10|\mathrm {sen} (2t)|$

que es una función oscilante, pero no sinusoidal, sino que va como el valor absoluto de un seno.

• Si $v_{0}=10$, la rapidez vale

$|{\vec {v}}|=10$

que es constante, lo que indica que en este caso el movimiento es uniforme.

• En el caso $v_{0}=8$ resulta una función oscilante

$|{\vec {v}}|={\sqrt {100\mathrm {sen} ^{2}(2t)+64\cos ^{2}(2t)}}={\sqrt {100-36\cos ^{2}(2t)}}$

Esta función varía desde 8m/s en el instante inicial (que es su rapidez mínima) a 10/m/s cuando el coseno se anula.

Archivo:Comparacion-rapidez.png

En concreto, para los tres instantes del enunciado tenemos la siguiente tabla de valores

$|{\vec {v}}|$	t=0	t=π/4	t=π/8
$v_{0}=0$	0.00	7.07	10.0
$v_{0}=10$	10.0	10.0	10.0
$v_{0}=8$	8.00	9.06	10.0

Componentes de la aceleración

Para hallar las componentes intrínsecas, en lugar de operar con expresiones dependientes del tiempo, vamos a calcular en primer lugar las velocidades y aceleraciones para los casos indicados y posteriormente calcularemos las componentes a partir de las proyecciones de los vectores.

Para la velocidad tenemos

${\vec {v}}=-10\,\mathrm {sen} (2t){\vec {\imath }}+v_{0}\cos(2t){\vec {\jmath }}$

y para las aceleraciones

${\vec {a}}=-20\,\mathrm {cos} (2t){\vec {\imath }}-2v_{0}\mathrm {sen} (2t){\vec {\jmath }}$

• En el caso $v_{0}=0$ queda

	t=0	t=π/4	t=π/8
v(m/s)	${\vec {0}}$	$-7.07{\vec {\imath }}$	$-10{\vec {\imath }}$
a(m/s²)	$-20{\vec {\imath }}$	$-14.1{\vec {\imath }}$	${\vec {0}}$

• En el caso $v_{0}=10$

	t=0	t=π/4	t=π/8
v(m/s)	$10{\vec {\jmath }}$	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -7.07\vec{\imath}+7.07\vec{\jmath}}	$-10{\vec {\imath }}$
a(m/s²)	$-20{\vec {\imath }}$	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -14.1\vec{\imath}-14.1\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -20\vec{\jmath}}

• En el caso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}

	t=0	t=π/4	t=π/8
v(m/s)	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 8\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -7.07\vec{\imath}+5.66\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -10\vec{\imath}}
a(m/s²)	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -20\vec{\imath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -14.1\vec{\imath}+11.3\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -16\vec{\imath}}

Aceleración tangencial

La aceleración tangencial la calculamos como la proyección de Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{a}} sobre Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{v}}

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a_t=\frac{\vec{a}\cdot\vec{v}}{|\vec{v}|}}

De las tablas anteriores podemos ver que en muchos de los casos solicitados esta cantidad es nula, por ser la aceleración ortogonal a la velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a_t}	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	14.1	0.0
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	0.0	0.0	0.0
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	0.0	3.98	0.0

En el caso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0} la velocidad es nula en t=0 y por ello la aceleración tangencial no está definida en ese instante.

Aceleración normal

El valor de la aceleración normal escalar lo podemos hallar de varias formas

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a_n=\frac{|\vec{v}\times\vec{a}|}{|\vec{v}|}=\sqrt{|\vec{a}|^2-a_t^2}}

De nuevo se anula en varios de los casos por ser la aceleración paralela a la velocidad

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle a_n}	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	0.0	0.0
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	20	20	20
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	20	17.7	16

Vectores tangente y normal

Vector tangente

El vector tangente es el unitario en la dirección de la velocidad, por lo que simplemente debemos dividir cada una de las velocidades anteriores por la rapidez correspondiente.

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{T}}	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -0.707\vec{\imath}+0.707\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -0.780\vec{\imath}+0.625\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}

Vector normal

El vector normal es el unitario en la dirección y sentido de la aceleración normal, por lo que solo hay que normalizar la tabla correspondiente

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{N}}	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	???	???
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -0.707\vec{\imath}-0.707\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\jmath}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\imath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -0.625\vec{\imath}-0.780\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -\vec{\jmath}}

Radio y centro de curvatura

Radio de curvatura

El radio de curvatura puede calcularse como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R = \frac{|\vec{v}|^2}{a_n}=\frac{|\vec{v}|^3}{|\vec{v}\times\vec{a}|}}

Lo que da la tabla

R	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \infty\,}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \infty}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	5	5	5
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	3.2	4.64	6.25

En el primer caso el radio de curvatura no está definido porque se trata de un punto en el que la partícula se da la vuelta en su movimiento. En el segundo caso resulta un valor constante como corresponde a un movimiento circular.

Centro de curvatura

Una vez que tenemos el radio de curvatura y el vector normal localizamos el centro de curvatura como

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_c = \vec{r}+R\vec{N}}

y resulta la tabla

Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{r}_c}	t=0	t=π/4	t=π/8
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=0}	???	???	???
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=10}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{0}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{0}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \vec{0}}
Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1.8\vec{\imath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 0.636\vec{\imath}-0.795\vec{\jmath}}	Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle -2.25\vec{\jmath}}

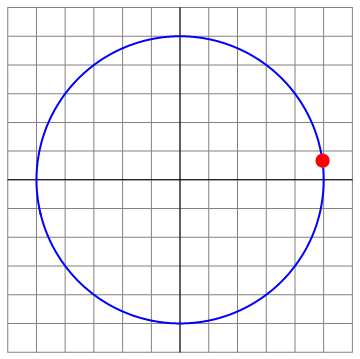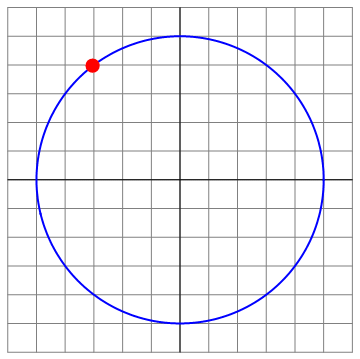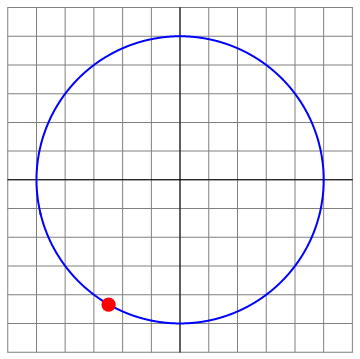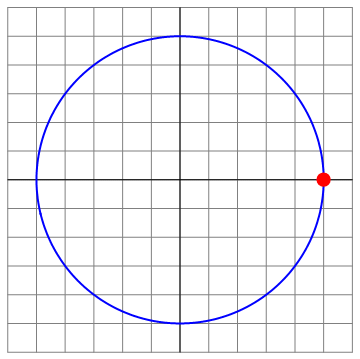
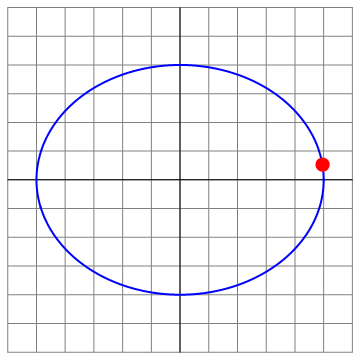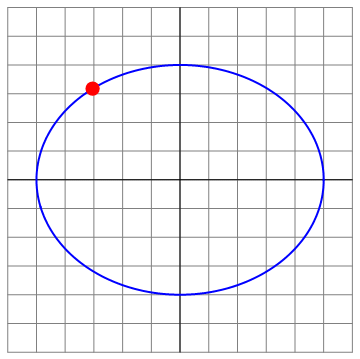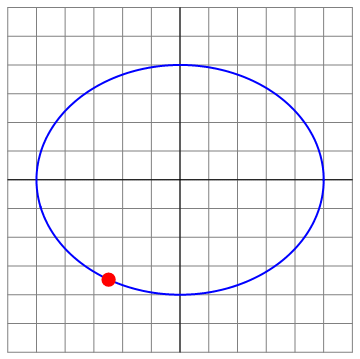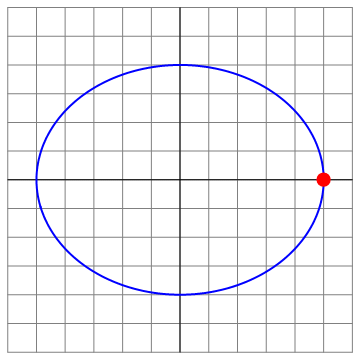
Podemos ilustrar las diferentes situaciones para el caso Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle v_0=8} , que es el menos trivial

t=0	t = π/8	t=π4
Archivo:OA3D-8-01.png	Archivo:OA3D-8-02.png	Archivo:OA3D-8-03.png